１から９までの妄想

「イチ、ニ、サン」という三個の数詞しかもたない民族がいるという。ただし、「サン」は「三以上たくさん」という意味だという。
「三と四」が区別できないのではなく、その必要がないからだと考えられている。
（古代の日本人も「ひ、ふ、み」という三個の数詞だけで生活していた時代があったのかも知れない。「ひ（hi）」と「ふ（hu）」は「ｈ」で始まるのに、「み（mi）」は「ｍ」から始まり、「み」は「ミナ、ミンナ、」に通じるからである。）
 
さらに、古代の日本人は「ひ、ふ、み、よ、い、む、な」という七個の数詞しかもたない時代があったのかも知れない。「七と八」の区別ができないのではなく、その必要がなかった時代のことを妄想するのである。
そんな時代において「八」は「たくさん」を意味したはずである。「八百屋」とか「八百万」といった言葉の中に、「たくさん」という意味として、その痕跡が残っているのではないのか。
また、「七」がたくさんを意味する「八」に近い最大の豊かさや幸を含む数詞として、「七福神」などの言葉に、その痕跡を残しているのかも知れない。
 
その後、「や（八）、こ（九）」が加わり、九以上を「たくさん」と表す時代が続く。「十」は「とうとう」の「とう」であり、「じゅう」ではなかった。（日本に漢数字が入ってくる奈良時代以降に「じゅう」になったと思われる。）
そして、時代は進み、「とう」も数詞に加わり、「とう余りいつ（十五）」などの表現にたどりつく。
　日本人は「十一」という数詞を増やす道は選ばなかった。
そして、「十（じゅう）」の先に「イレブン」という数詞を増やした民族は十二進法の中にその痕跡を残すことになる。
 
現在、世界で用いられている十進法は人間の手の指が両手で「十（じゅう）」だからだと言われている。両手を広げて相手に示した「たくさん」を表す「十（じゅう）」は、売買契約の成立と親睦を表したことだろう。
その意味で、相手と共に数える場合は「グー」から始めて指を広げていく動作になる。幼児が問われて「三歳！」と示す指の形を見れば納得できるのではないか。
 
ところが、一人で心密かに数える場合は「指折り」数えるのである。損得勘定や恋しい人を待つ場合は「パー」から始めて「一、二、三、・・」と数える。
 
最近では、「グー」から数えるのは「競り」のような場合だけで、ほとんどの場合は「パー」から始まるような気がする。相手やみんなと共に数えるのは、ロケットの打ち上げや、楽天球場での「三、二、一、バーン」という勝利宣言のような時だけかも知れない。

以上は音韻について何も知らない者の妄想である。

妄想は「１＋２＝３」という数式にも及ぶ。自然数「１，２，３」という「奇数から始まる連続する三個の数の関係」を示す式からの妄想である。
「３、４、５」は「２番目」のそうした三個の数であり、関係式は「２乗」を用いて、「３＾２＋４＾２＝５＾２」と表せる。（これは正しい）

「５，６，７」は「3番目」のそうした三個の数であり、関係式は「３乗」を用いて、「５＾３＋６＾３＝７＾３」と表せる。
この数式は「フェルマーの最終定理」をもちだすまでもなく誤りである。
しかし、左辺は１２５＋２１６＝３４１であり、右辺の３４３に近い。
ここで、「差の割合」を「差÷右辺の数」と定めると、この場合の差の割合は「２÷３４１＝０．００５８６５・・・」である。

そこで、次のような妄想をいだくことになる。
「ｎ番目」の奇数を「２ｎ−１」として、連続する三数の間において、「差の割合」が最小になるのは、次の式で「ｍ＝ｎ」の時である、という仮説である。
左辺＝（２ｎ−１）^ｍ＋（２ｎ）^ｍ　　　　右辺＝（２ｎ＋１）^ｍ

例として試行してみる。
「４番目（ｎ＝４）」の三つ数字は「７、８，９」であり、左辺「７^４＋８^４」と右辺「９^４」の差は「６４」であり、差の割合は「０．００９７５４６・・」である。
ｍの値を「１，２，３，４，５」とした時の「差の割合」は次の通りであり、ｍ＝４の時が最小である。
ｍ＝１の時　　７＋８　と　９　の差は６で、差の割合は０．６６６・・
ｍ＝２の時　　７^２＋８^２　と　９^２　の差の割合は０．２７１・・
ｍ＝３の時　　７^３＋８^３　と　９^３　の差の割合は０．１７２・・
ｍ＝４の時　　７^４＋８^４　と　９^４　の差の割合は０．００９・・
ｍ＝５の時　　７^５＋８^５　と　９^５　の差の割合は０．１６０・・

ｘ^４＋ｙ^４＝ｚ^４
これを満たす自然数ｘ、ｙ、ｚは存在しないが、「奇数から始まる連続する三個の自然数」という条件を外せば、正解に近い「ニアミス解」が存在する。
例えば、「167^4＋192^4 ≑ 215^4」は、ほぼ等式に近い。等式になるのは「215.00000482976324」の４乗である。
また、「1125^5＋2335^5＝(2347.0000000364907)^5」であり、自然数解でなければ「正解」は存在するのである。
 
このような所にも自然数と有理数の違いが現れる。そして、その違いの表れの中に「自然数の不思議さ」がひそんでいるのである。 

　フェルマーの最終定理が証明される１９９５年以前においては、「反例」や「反例にちかいもの」を示そうと多くの数学者が探索を進めた。 
その一人が「インドの魔術師」とも呼ばれる数学者ラマヌジャン（１８８７～１９２０）である。
　ラマヌジャンはフェルマーの最終予想の「反例に近いもの」を探していて、その途中で「1729」という自然数に出会う。
自然数「1729」は二種類の「二個の三乗和」で表される最小数で「9^3＋10^3=12^3＋1^3」になることを発見したのである。
その後、「X^3+Y^3=Z^3+W^3」という一般形について研究し、１９１３年に無限個の解を与える公式を発見し、「楕円曲線」、「楕円曲面」の理論にまで発展させたという。
 
自然数「1729」は「タクシー数」と呼ばれることもあるが、その発見の経緯は不明のまま、偶然にも公表されることになる。
１９１８年２月のことで、ラマヌジャンの才能を見抜いてケンブリッジ大学に招聘したイギリス人数学者ハーディが、療養所のラマヌジャンを見舞った際に偶然明らかになった。（ハーディが乗ったタクシーのプレート番号が「1729」であったことからラマヌジャンが話したのである。）
しかし、なぜラマヌジャンがその数字のことを知っていたのか、その理由が明らかになるのは、ラマヌジャンが亡くなった後の２０１３年のことで、ラマヌジャンが残した「ノートブック」を整理して明らかになったのである。
 
ラマヌジャンはたくさんの定理を直感的に発見し、証明することについては頓着しなかったという。自然数「1729」の発見もその類と見られていたのである。そして、もちろん直感的なひらめきに依るところも大きい。

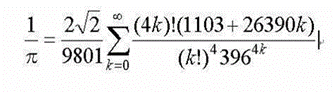
ラマヌジャンの直感的なひらめきがどんなものなのか、は想像することさえ難しい。上の円周率に関する式は正しいことが証明されているが、ラマヌジャンの考え方については残された「ノートブック」から推測されるだけである。（今日でいうモジュラー関数と呼ばれるものを研究した成果だという。）
 
「１から９までの妄想」から生まれた「仮説」が思いもよらない所まで関係していることが分かる。
そして、おなじみの三平方の定理に当てはまる「２乗」の式・・・・・・「3^2+4^2=5^2」に続くような「３乗」の式「5^3+6^3=7^3−2」に愛着を憶える。
そして、「３乗」の式が切り開く「楕円曲線」や「楕円曲面」に思いを寄せる。その突破口にあるのがタクシー数「1729」であり、２種類の３乗数の和「9^3+10^3=12^3+1^３」なのである。
（なお、実数平面上の楕円曲線とは「y2=x3+ax+b」で表される曲線である。）