偶数と奇数（１）

自然数（１、２、３、・・・）を、偶数と奇数に分けて考え始めたのはいつ頃のことだったのだろうか。記録に残っているものでは、古代ギリシャ時代のピタゴラス学派によるものだという。
また、他説によれば、偶数の源は「ペア」であり、古代ギリシャ時代より遥かに遠い時代に遡るはずだ、という。
そして、偶数、奇数に付随する「文化的な意味」は、今日まで続いている。
 
＜偶数と奇数の文化＞
例えば、日本では「奇数」が「善」で、祝金の額は「一、三、五」がヨシとされる。
それに対して、西洋では「偶数」は対称（シンメトリー）であり、「美と調和」の象徴と捉えられている。また、「奇数」は分解できない存在であり、そのままで「完全」であるという捉え方もあるという。 
一から十までの自然数の中で考えれば、「ペア」の概念は強く働いたと考えられ、偶数、奇数の区別は、数字の発生と時を同じにしていたのかも知れない。
しかし、自然数はどんどん大きな数を表すようになり、「限りなく続くモノ」の象徴にさえなる。そんな自然数は、まるごと「自然数全体の集合：Ｎ」などと呼ばれ、数学の一つの世界として対象化されるようになる。
 
＜偶数と奇数の学習＞
現在の日本では、自然数を偶数と奇数に分けて考える指導を小学五年生に配当している。「偶数＋奇数」は偶数にはならい、とか「偶数×奇数」は偶数になる。そんなことについて学ぶのである。
「132×143」の結果は「偶数だろうか、奇数だろうか？」
 
偶数と奇数の区別は比較的容易である。大きな自然数であっても、「一の位」で判断することができるからである。
 
＜剰余類＞
さて、この「偶数と奇数に分ける」という考え方は、自然数全体を「偶数の集合」と「奇数の集合」に二分することになる。そして、偶数は２で割って余りが「０」であり、奇数は余りが「１」である、という「剰余類」の概念に辿り着く。
そして、極論すれば、自然数全体の加法や乗法の計算は次の二つの表で表すことができることになる。

＜偶数＋奇数＝奇数＞

＜偶数×奇数＝偶数＞

「132」は偶数であり、「143」は奇数であるので、「132≡0 mod2」、「143≡1 mod2」となる。それで、和は「1+0=1」に帰着されて「奇数」であることが分かり、積も「1×0=0」から「偶数」であることが分かる。

＜二進記数法＞ 
そして、この「０と１」の演算は、「二進記数法」を誕生させることになる。二進記数法の生みの親はライプニッツ（１６４６～１７１６）だという。「1+1=2」と「1+1=0」を重ね合わせて考えることにするのである。
さらに、十進記数法が「・・・+a・10＾3+b・10＾2+c・10+d・1」と表されることから、「10=n」と置くと「・・・+a・n＾3+b・n＾2+c・n+d・1」となる。これを「ｎ進記数法」と呼び、「n=2」と置けば「二進記数法」のできあがりである。

例えば、「101」と「111」の加法と乗法も前出の二つの表によって求めることができる。（ちなみに、「101」は５の二進記数法表示であり、「111」は７の二進記数法表示である。）

＜５＋７＝１２の二進記数法＞

＜５×７＝３５の二進記数法＞

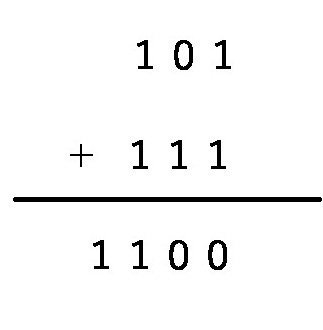
これまでの論述は、自然数を偶数と奇数に「二分する」考え方のスバラシサと有効性の一端を示すことである。
 
＜３で割る場合＞
それでは「132」と「143」の積は、「２で割る」のではなく、「３で割る」と余りはいくつ？になるのか。「４で割る」と余りは？「５で割る」と、・・・と設問は続くことになる。
 
例として、「３で割る」場合を考える。余りは「０か１か２」の三種類である。それで、自然数を余りの数で三種類（剰余類）に分けて考えることにする。

これは、上図のように、自然数を一行に並べるのではなく、また二行に並べるのでもなく、三行に並べることに対応している。（なお、○印の数字は「素数」であり、素数の現れ方にも注意したい。）
 
「３で割る」場合の自然数は次のように三分類される。
1≡4≡7≡10≡・・・≡130≡・・・・　→１
2≡5≡8≡11≡・・・≡・≡143≡・・　→２
3≡6≡9≡12≡・・・≡132≡・・・・　→０
 
そして、加法と乗法は次の表に従うことになる。

＜０＋２＝２＞

 

＜0×２＝０＞

したがって、「132×143」の積は「３で割る」と余りは「０」で割り切れることが分かる。
 
「132」と「143」のように三桁の数字なら積を計算で求め、それを「３で割る」方が、余りの求め方としては簡単かもしれない。ところが、自然数にはいくらでも大きい数があるのである。

＜難問への活用・・・１２で割る場合＞
また、入学するのに難しいとされる「灘中」の１９９９年の入試問題の一つに次のような問題があるという。
 
Ａ・・・1, 2, 3, 4, 5, ・・・,999
Ｂ・・・1998, 1997, 1996,・・・,1003, 1002, 1001, 1000
ＣはＡとＢを順序正しく掛けてできる「999」個の積である。
さて、Ｃの中には「12で割り切れる」ものは何個あるか？
 
Ａ、Ｂの数を「12で割って余る数」に変換すると、次のようになる。
Ａ→1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2,3,・・・0, 1, 2, 3
Ｂ→6, 5, 4, 3, 2, 1, 0, 11, 10, 9, 8, 7, 6, 5,4,・・・7, 6, 5, 4
それで、Ｃは次のような数字が並ぶことになる。
　Ｃ→6, 10, 0, 0, 10, 6, 0, 4, 6, 6,4, 0, 6, 10, ・・・0, 6, 10, 0
上のＣの太字部分には「０が４回」あり、それが「83回」繰り返し、残りが「6,10,0」である。
　したがって、「4×83+1=333」個が「12で割り切れる」ことになり、「999」個の「１／３」に当たる。これは、最初の太字の「12個」の中に、「12で割り切れるものが「１／３」の「４個」であったことと同じ割合であったことになる。