今日の最大・最小 240216
最大値、最小値を求めよ、とりうる値の範囲を求めよ、という問題は多いです。関数関係が見つかった、関係式が見つかったときに、range を調べたくなる感覚は数学のよさの一つだと思います。
前回と同じ問題
半径1 の円周上に3点A, B, C があります。内積 $${\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}}$$ の最大値と最小値を調べてみましょう。(2020 一橋大)
今回はベクトルをメインに使って調べてみます。
円の中心をO として、
O を基点とする A, B, C の位置ベクトルをそれぞれ $${\vec{a}}$$, $${\vec{b}}$$, $${\vec{c}}$$ とします。
$${|\vec{a}|=|\vec{b}|=|\vec{c}|=1}$$ が成り立ちます。
$${\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}=(\vec{b}-\vec{a})\cdot(\vec{c}-\vec{a})}$$$${=1-\vec{a}\cdot(\vec{b}+\vec{c})+\vec{b}\cdot\vec{c}}$$
式を見ても、(式を見るまでもないのですが) $${\vec{b}}$$ と $${\vec{c}}$$ については対称性があります。
一般に $${|\vec{b}+\vec{c}|^2=|\vec{b}|^2+|\vec{c}|^2+2\vec{b}\cdot\vec{c}}$$ が成り立ちますから、
$${\vec{b}\cdot\vec{c}=\frac{1}{2}|\vec{b}+\vec{c}|^2-1}$$
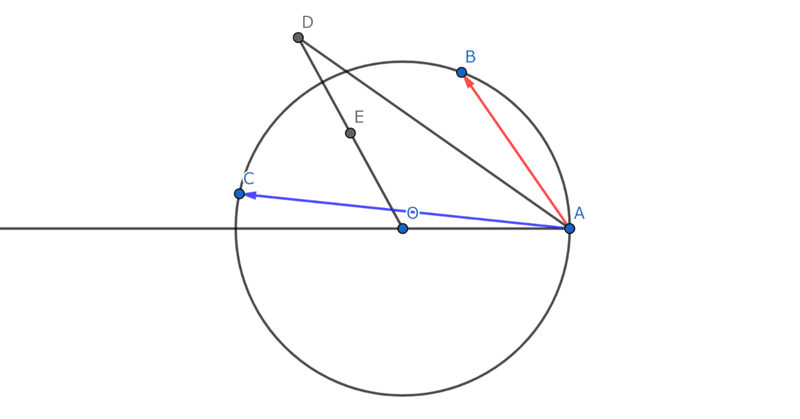
$${\vec{b}+\vec{c}=\overrightarrow{\rm OD}}$$ なる点D をとって、位置ベクトルを$${\vec{d}}$$ とします。
D は 菱形 OBDC を形作ることに注意します。
$${\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}=\frac{1}{2}|\vec{d}|^2-\vec{a}\cdot\vec{d}}$$$${=\frac{1}{2}|\vec{d}-\vec{a}|^2-\frac{|\vec{a}|^2}{2}}$$
$${=\frac{1}{2}{\rm AD}^2-\frac{1}{2}}$$
結局 AD の長さのとりうる値の範囲を調べることになりました。
D は 菱形OBDC の頂点でした。
弦BC の中点を E とすると、$${\overrightarrow{\rm OD}=2\overrightarrow{\rm OE}}$$ です。
E が 線分OAの中点と一致するとき、すなわち D が A と一致するとき、
AD の長さは 0 となり、AD の長さは最小です。内積は最小値$${-\frac{1}{2}}$$ をとります。
ちなみに、これは 菱形OBDC (OBAC) は 2つの三角形OAB, OAC が正三角形になるときです。
$${\overrightarrow{\rm OE}=-\overrightarrow{\rm OA}}$$ のとき、すなわち、B, C が一致して、$${\overrightarrow{\rm OB}=\overrightarrow{\rm OC}=-\overrightarrow{\rm OA}}$$ のとき、$${\overrightarrow{\rm OD}=-2\overrightarrow{\rm OA}}$$、AD の長さが 3 で最大です。内積は最大値 4 をとります。このときのD を $${{\rm D}_0}$$ とします。
最大となる説明をつけたほうがよいと思います。
$${{\rm E}_0}$$ を 直径$${{\rm AE}_0}$$ の端点とします。
E が直線OA 上にあって、$${{\rm E}_0}$$でないとします。円外にとることはできません。直径上にあるときは AD の長さは $${{\rm AD}_0}$$ より短くなります。
E が直線OA 上にないときを調べます。二等辺三角形OBC が合同であれば、OD の長さは等しいので、角AOD が大きい方が AD の長さは長くなります。
つまり、合同な二等辺三角形OBC については、Eが(すなわちDが)直線OA上にあるときが最も大きくなります。
したがって、Dが $${{\rm D}_0}$$ のとき最大であることになります。
この記事が気に入ったらサポートをしてみませんか?
