今日の式の処理 240228

問題解決のアプローチを考えていると、これどう処理すればいいのか？ という場面に出会います。

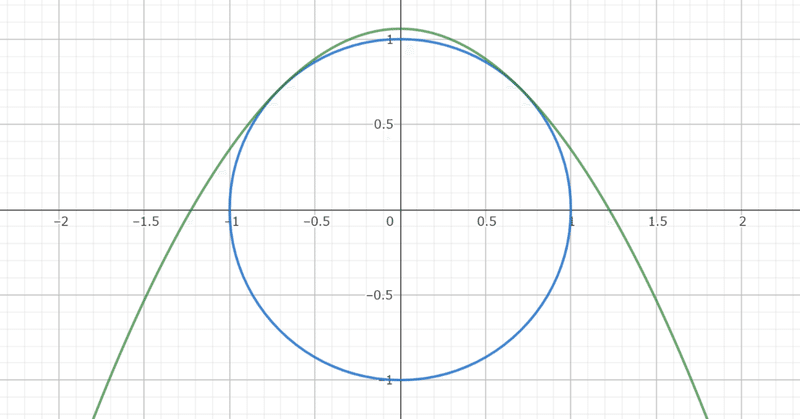
座標平面上で、放物線 C: $${y=ax^2+bx+c}$$ が 2点 P$${(\cos\theta,\sin\theta)}$$, Q$${(-\cos\theta,\sin\theta)}$$ を通り、点P と 点Q のそれぞれにおいて円 $${x^2+y^2=1}$$ と共通の接線を持っています。ただし、θ の大きさは 0度より大きくて90度より小さいとします。
(1) a, b, c を $${s=\sin\theta}$$ を用いて表してください。
(2) 放物線 Cと x 軸で囲まれた図形の面積 A を s を用いて表してください。
(3) $${A\geqq \sqrt{3}}$$ を示してください。　(東京大2024)

View this post on Instagram

A post shared by Minamiazabu Hiroo official (@minamiazabu_math)

東大らしいシンプルで美しい問題です。面積 A の最小値は $${\sqrt{3}}$$ らしいですが、これがまた θ が 45度で、というのが美しいです。以下、略解です。

P と Q は y 軸に関して対称ですから、放物線 C の軸は y 軸です。したがって、b は 0 です。
P$${(\sqrt{1-s^2},s)}$$ における円の接線の傾きと放物線 C の Pにおける接線の傾きが等しいので、
$${2a\sqrt{1-s^2}=\dfrac{-\sqrt{1-s^2}}{s}}$$
また、P は 円と放物線の共有点ですから、
$${a(1-s^2)+c=s}$$
したがって、$${a=\dfrac{-1}{2s}}$$, $${b=0}$$, $${c=\dfrac{1+s^2}{2s}}$$

C と x 軸との共有点の x 座標を α とします。(正のものをとります。)
このとき、$${\displaystyle{A=2\int_0^\alpha(ax^2+c)\ dx=\dfrac{2\alpha^3}{3s}}}$$
ここで、$${a\alpha^2+c=0}$$ ですから、 $${\alpha^2=\dfrac{-c}{a}=1+s^2}$$
したがって、$${A=\dfrac{2(1+s)^{\frac{3}{2}}}{3s}}$$
ここまでは、スムーズにたどり着きます。

A のとりうる値の範囲を調べるには、式をどう処理しましょうか？いろいろな方法がありそうです。
$${B=\dfrac{s^2}{(1+s^2)^3}}$$ を調べることにします。
$${t=1+s^2}$$ とおいて、$${B=\dfrac{t-1}{t^3}=\dfrac{1}{t^2}-\dfrac{1}{t^3}}$$
さらに、$${x=\dfrac{1}{t}}$$ とおいて、$${B=x^2-x^3}$$
$${\dfrac{1}{2}\lt x\lt 1}$$ でのとりうる値の範囲を調べます。
$${\frac{dB}{dx}}$$ をみると B は $${x=\dfrac{2}{3}}$$ で最大値 $${\dfrac{4}{27}}$$ をとることが分かります。
したがって、A は $${s=\dfrac{\sqrt{2}}{2}}$$ (θ = 45° )で 最小値 $${\sqrt{3}}$$ をとることが分かります。