【今日の計算】3次関数のグラフと接線で囲まれる部分の面積 240222

$${f(x)=x^3-3x+2}$$ とします。α を 1より大きな実数とします。
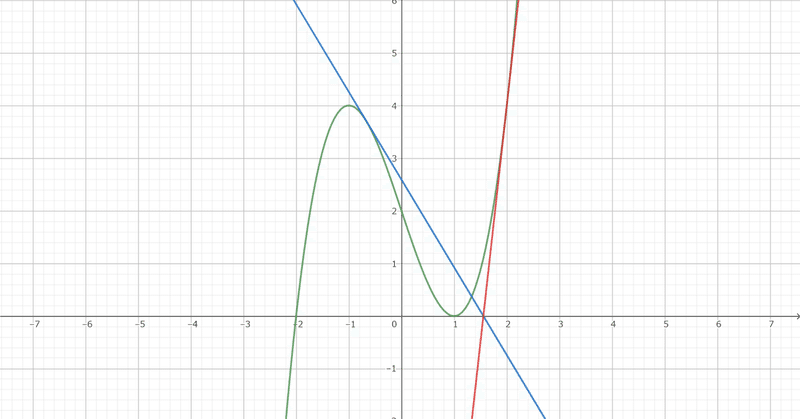
曲線 C: y = f(x) 上の点P (α, f(α)) における接線と x 軸との交点を Q とします。
点 Q を通る C の接線の中で傾きが最小のものを ℓ とします。
(1) ℓ と C の接点の x 座標を α の式で表してください。
(2) α = 2 とします。ℓ と C で囲まれた部分の面積を求めてください。
(2019 一橋大)

おそらく流れは一つかと思いますが、計算を工夫してみましょう。

まず、P における接線の方程式を求めます。
$${f(\alpha)=\alpha^3-3\alpha+2}$$, $${f^\prime(\alpha)=3(\alpha^2-1)}$$ ですから、
$${y=3(\alpha^2-1)x-2(\alpha^3-1)}$$ 暗算でいきたいですね。どうやらこの変形のほうが楽でした。
Q の x座標は $${\alpha-1\not=0}$$ に注意して、$${\dfrac{2(\alpha^2+\alpha+1)}{3(\alpha+1)}}$$

T(t, f(t)) における接線の方程式は (1) と類似で、
$${y=3(t^2-1)x-2(t^3-1)}$$
Q を通るので、$${\dfrac{(t^2-1)(\alpha^2+\alpha+1)}{\alpha+1}-(t^3-1)=0}$$
整理すれば、$${t^3-at^2+a-1=0}$$ …①ここで、$${a=\dfrac{\alpha^2+\alpha+1}{\alpha+1}}$$
C は x 軸と (1, 0) で接しています。
すると、Q を通る C の接線はすぐに2つわかって、それは、
(1, 0 ) を通るもの　傾きは 0 です。
P を通るもの 傾き $${3(\alpha^2-1)}$$ いまの場合 正の数です。
① の方程式の解は 1, α ともう一つあって それを β とすると、
解と係数の関係から$${1+\alpha+\beta=a}$$
つまり $${\beta=\dfrac{a^2+\alpha+1}{\alpha+1}-(\alpha+1)=\dfrac{-\alpha}{\alpha+1}}$$
このとき、$${\beta^2-1=\dfrac{\alpha^2}{(\alpha+1)^2}-1=\dfrac{-2(\alpha+1)}{(\alpha+1)^2}}$$
いまの場合、傾き$${f^\prime(\beta)\lt 0}$$
したがって、ℓ と C の接点の x 座標は β すなわち $${\dfrac{-\alpha}{\alpha+1}}$$ … (1) 答え

(2) に進みます。
α は 2 ですから、上の β は $${\beta=-\dfrac{2}{3}}$$ です。
接線 ℓ を $${y=mx+n}$$、 C と ℓ の接点以外の共有点の x 座標を γ とおくと求める面積は、
$${S=\int_\beta^\gamma((mx+n)-f(x))\ dx}$$ で計算することができます。
これで、解決の見通しが立ちました。あとはただの計算ですので、工夫してみましょう。
γ は 方程式 $${f(x)=mx+n}$$ の解ですが、この解は β、β、γ の3つです。解と係数の関係から和は 0 だとわかりますから、$${\gamma=-2\beta=\dfrac{4}{3}}$$

このとき、
$${(mx+n)-f(x)=-(x-\beta)^2(x-\gamma)}$$ …②ですから、
$${S=-\int_\beta^\gamma(x-\beta)^2(x-\gamma)\ dx}$$
面積は平行移動で変わりません。
$${S=-\int_0^{\gamma-\beta}x^2(x-(\gamma-\beta))\ dx}$$
ここで、$${\gamma-\beta=2}$$
つまり、$${S=-\int_0^2x^2(x-2)\ dx}$$
$${=\left[-\dfrac{1}{4}x^4+\dfrac{2}{3}x^3\right]_0^2=\dfrac{4}{3}}$$ … (2) 答え

このように、実は接線の方程式を具体的に求めなくても、接点が2重解であることを知っていればほぼ暗算で解けてしまいます。
答案では 接線 ℓ の方程式くらいは書いたほうがいいかもしれませんが、出題者は当然この裏話を知っているはずです。
具体的な計算をやって、②のように因数分解できた というより、
因数分解できることを知っていると計算は全然簡単になります。
この手の問題を初めて解いたという人ならいざ知らず、経験があるなら知恵にしてしまっていいと思います。
高校の数学では、解と係数の関係も同じかもしれません。