薄板の変形解析
薄板の薄板について、板4辺を固定し均一の面圧をかけたときの板中央部の変位を解析しました。
文献:「例題で極める非線形有限要素法 CAEで正しい結果を導くためのトレーニング」
著:渡辺浩志、出版:丸善出版
[CS07-06] つりあげ効果
<動作確認環境>
Salome-Meca 2019 (CAELinux2020Lite+VirtualBox)
Salome-Meca 2021 for windows(OS :Windows11)
1.解析対象
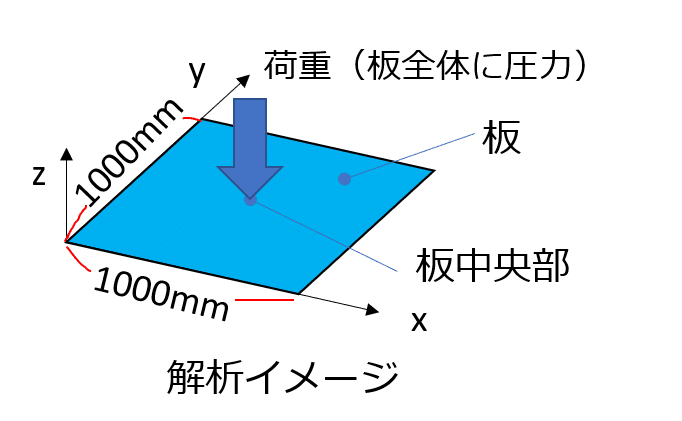
下図に解析モデルを示します。
1.1 モデル寸法・物性値
板:1m(1000mm)角、厚さ1mm
板にかける面圧 5Pa(5x10-6 N/mm2)
物性値:70000MPa、ポアソン比0.3(アルミニウム相当)
1.2 解析モデル
メッシュ:四角形1次要素(シェル要素:DKT要素、coque_3D)
拘束条件:板の4辺固定(x,y,z方向固定)
解析:①線形解析、②非線形解析(大変形)
出力:板中心の変形
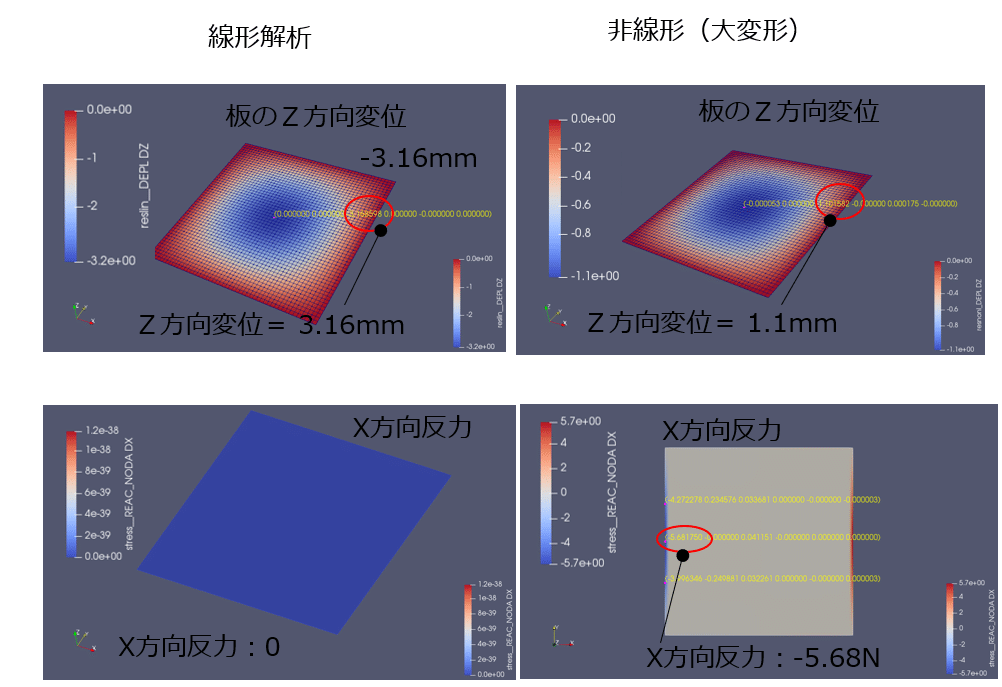
2.解析結果
板中心の変形は、線形解析3.16mm(変位だと-3.16mm)に対して非線形解析1.1mm(変位だと-1.1mm)が小さい結果でした。
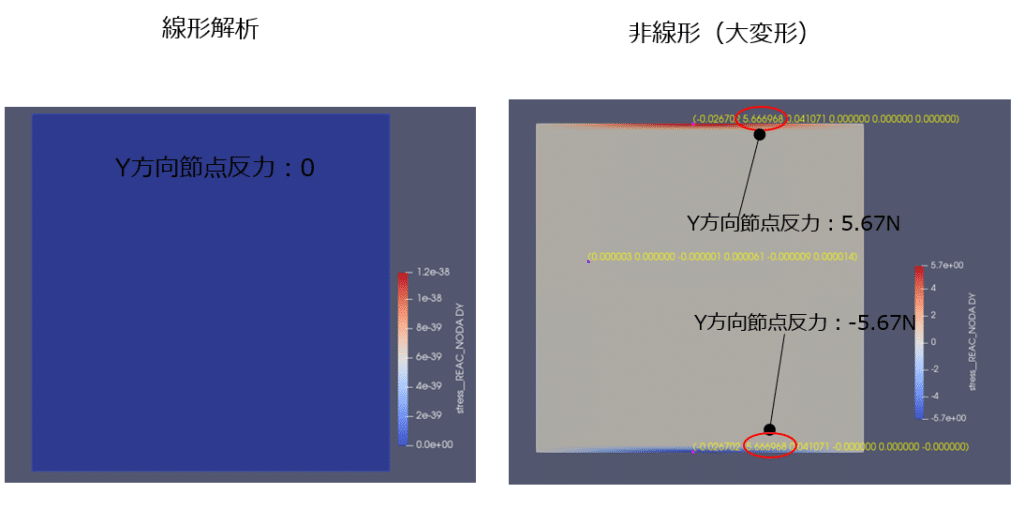
3.公式による比較
機械便覧に今回の事例における公式がありましたので計算をしました。
機械便覧によると、平板が板厚の半分以上の場合、たわみと面内変形を考慮する必要がありようです。計算した結果、大変形解析での計算結果が公式と近い計算結果でした。
板中心位置のたわみは、Wmax=α2 x P x a4/(Exh3)α2:たわみ係数0.016(α03-55図5・15長方形板NO1~NO8のたわみ係数αi,’αi’から読み取り)P:面圧(N/mm2)、a:板幅(mm) 、E:ヤング率(N/mm2) h:板厚(mm) 引用元:機械便覧α3編 材料力学 α03-54, α03-55(日本機械学会)
公式による計算結果: Wmax=0.016x 5 x 10-6 x 1000 4/(70000x13)=1.143mm
この解析とある勉強会で発表しました。その際、薄板曲げに関することがあるので確認するよう助言がありましたでやってみました。振り返ると大学生のころに購入した材料力学の本にも記載がありました。
4. まとめ
板厚に対して十分に薄い板についてはシェル要素による解析、たわみが板厚に対して半分以上の場合大変形を考慮した解析が必要となります。今回、私が実際に計算した気づきです。
シェル要素は普段業務では使わないので、気が付いたらトライしようと思います。
補足
その1:線形解析(commファイル)
線形解析による計算コマンドです。
DEBUT(identifier='0:1',
LANG='EN')
mesh = LIRE_MAILLAGE(identifier='1:1',
UNITE=20)
model = AFFE_MODELE(identifier='2:1',
AFFE=_F(MODELISATION=('DKT', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
shell = AFFE_CARA_ELEM(identifier='3:1',
COQUE=_F(EPAIS=1.0,
GROUP_MA=('Plate', )),
MODELE=model)
al = DEFI_MATERIAU(identifier='4:1',
ELAS=_F(E=70000.0,
NU=0.3))
fieldmat = AFFE_MATERIAU(identifier='5:1',
AFFE=_F(MATER=(al, ),
TOUT='OUI'),
MAILLAGE=mesh,
MODELE=model)
load = AFFE_CHAR_MECA(identifier='6:1',
ARETE_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('Edge_1', 'Edge_2', 'Edge_3', 'Edge_4')),
MODELE=model,
PRES_REP=_F(GROUP_MA=('Plate', ),
PRES=5e-06))
reslin = MECA_STATIQUE(identifier='7:1',
CARA_ELEM=shell,
CHAM_MATER=fieldmat,
EXCIT=_F(CHARGE=load),
MODELE=model)
stress = CALC_CHAMP(identifier='8:1',
CARA_ELEM=shell,
CHAM_MATER=fieldmat,
CONTRAINTE=('SIGM_ELNO', ),
CRITERES=('SIEQ_ELNO', ),
FORCE=('FORC_NODA', 'REAC_NODA'),
MODELE=model,
RESULTAT=reslin,
TOUT_ORDRE='OUI')
unnamed0 = POST_CHAMP(identifier='9:1',
EXTR_COQUE=_F(NIVE_COUCHE='SUP',
NOM_CHAM=('SIGM_ELNO', 'SIEQ_ELNO'),
NUME_COUCHE=1),
RESULTAT=stress)
Final = CALC_CHAMP(identifier='10:1',
CARA_ELEM=shell,
CONTRAINTE=('SIGM_NOEU', ),
CRITERES=('SIEQ_NOEU', ),
RESULTAT=unnamed0,
TOUT_ORDRE='OUI')
IMPR_RESU(identifier='11:1',
FORMAT='MED',
RESU=(_F(MAILLAGE=mesh,
RESULTAT=stress),
_F(MAILLAGE=mesh,
RESULTAT=reslin)),
UNITE=2)
FIN(identifier='12:1',
)
その2: 非線形解析(commファイル)
SalomeMecaで非線形解析を行う場合は、非線形解析の指定で緑マーカー部による非線形解析と変形が大変形であることの指定、 青マーカー部による荷重を段階的にかける指定が必要です。非線形解析はSalomeMecaの初期条件では収束しないことがあるので、 赤マーカーによるパラメータ指定が必要です。(本解析では必要でしたが、他の解析では不要だったり必要になったりケースバイケースです)
DEBUT(LANG='EN')
mesh = LIRE_MAILLAGE(UNITE=3)
model = AFFE_MODELE(AFFE=_F(MODELISATION=('DKT', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
shell = AFFE_CARA_ELEM(COQUE=_F(EPAIS=1.0,
GROUP_MA=('Plate', )),
MODELE=model)
al = DEFI_MATERIAU(ELAS=_F(E=70000.0,
NU=0.3))
fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(al, ),
TOUT='OUI'),
MAILLAGE=mesh,
MODELE=model)
func = DEFI_FONCTION(NOM_PARA='INST',
VALE=(0.0, 0.0, 1.0, 1.0))
step = DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=1.0,
NOMBRE=50))
load = AFFE_CHAR_MECA(MODELE=model,
PRES_REP=_F(GROUP_MA=('Plate', ),
PRES=5e-06))
fix = AFFE_CHAR_MECA(ARETE_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('Edge_1', 'Edge_2', 'Edge_3', 'Edge_4')),
MODELE=model)
resnonl = STAT_NON_LINE(CARA_ELEM=shell,
CHAM_MATER=fieldmat,
COMPORTEMENT=_F(DEFORMATION='GROT_GDEP',
RELATION='ELAS',
TOUT='OUI'),
CONVERGENCE=_F(ITER_GLOB_MAXI=200,
RESI_GLOB_RELA=5e-05),
EXCIT=(_F(CHARGE=load,
FONC_MULT=func),
_F(CHARGE=fix)),
INCREMENT=_F(LIST_INST=step),
METHODE='NEWTON',
MODELE=model,
NEWTON=_F(MATRICE='TANGENTE',
REAC_INCR=1,
REAC_ITER=1),
SOLVEUR=_F(METHODE='MUMPS'))
stress = CALC_CHAMP(CARA_ELEM=shell,
CHAM_MATER=fieldmat,
CONTRAINTE=('SIGM_ELNO', ),
CRITERES=('SIEQ_ELNO', ),
FORCE=('FORC_NODA', 'REAC_NODA'),
MODELE=model,
RESULTAT=resnonl,
TOUT_ORDRE='OUI')
unnamed0 = POST_CHAMP(EXTR_COQUE=_F(NIVE_COUCHE='MOY',
NOM_CHAM=('SIGM_ELNO', 'SIEQ_ELNO'),
NUME_COUCHE=1),
RESULTAT=stress)
Final = CALC_CHAMP(CARA_ELEM=shell,
CONTRAINTE=('SIGM_NOEU', ),
CRITERES=('SIEQ_NOEU', ),
RESULTAT=unnamed0,
TOUT_ORDRE='OUI')
IMPR_RESU(FORMAT='MED',
RESU=(_F(MAILLAGE=mesh,
RESULTAT=Final),
_F(MAILLAGE=mesh,
RESULTAT=resnonl)),
UNITE=80)
FIN()
