Raspberry Piに距離センサーHC-SR04を付けて測定距離をLCDに表示してみる：キャリブレーション（Python）

　前回Raspberry Piに距離センサーHC-SR04を取り付けて距離を測定、LCDに結果を表示する所まで作ってみました：

しかし、実際に測定してみると真の距離に対して測定距離（超音波が飛んだ時間に音速を掛け算した距離）がズレる問題が発生しました。その理由は前回の記事の終わり辺りに記載していますが、まぁ…当たり前なんですね(^-^;

　距離センサーにこちらが思う距離をちゃんと測定してもらうにはキャリブレーションが必要です。そこで今回はキャリブレーションを行うプロセスを追加して、測定誤差を減らす試みをしてみます。

キャリブレーションの仕方

距離センサーと利用者の原点は普通異なる

　具体的なキャリブレーションの仕方から見て行きましょう。まず大前提として、距離センサーに対する「原点」を利用者側で決める必要があります。例えば以下の異なる位置にセンサーが取り付けられた2つのフレームを見て下さい：

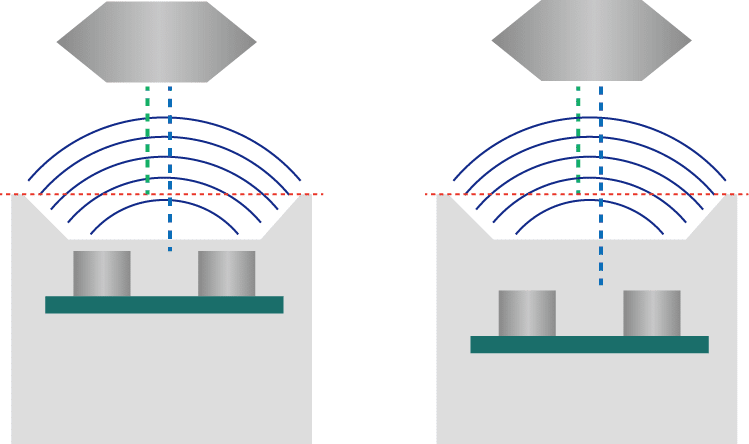
　利用者が想定する原点はオレンジの横線で、測定して欲しい真の距離は原点から対象物まで伸びた緑色のラインです。しかしフレーム内の距離センサーは青縦線の「距離センサーが思う測定距離」を返します。当然測定距離は見当違いになります。センサーの取り付け位置によっても変わりますから、取り付け誤差もここには含まれてしまいます。

測定距離と真の距離のデータセットを沢山サンプリング

　そこで次のようにキャリブレーションするデータを取ります。まず利用者が想定する原点（オレンジの横線）を決めます。次にその原点からある正確な距離だけ離れた所にターゲットを置きます。この既知の距離を真の距離（Dtrue）と定義します。図で言うと緑色の縦ラインがそれに該当します。続いて同じターゲットを距離センサーで測定し、その測定距離Dm（青い縦ライン）を計測します。センサーから求められるのは時間だけなので、適当な音速を掛けて単位を合わせます。

　これでDmに対するDtrueのデータが一セット揃いました。もし実際の測定結果がDmと出たら、利用者には「Dtrueでした」と返せば、利用者からすると正確な距離を出してくれたように見えますよね。

　同じようなデータセットを様々なターゲット距離でサンプリングすれば、測定距離Dmと真の距離Dtrueとの関係性が見えてくるわけです。その関係性を利用すれば、任意の測定距離に対してらしい真の距離を求める事が出来るようになります。これがキャリブレーションです。

測定距離を安定化させるために

　上で説明した測定距離と真の距離のデータセットを取るには、測定距離が安定しないといけません。通常距離センサーは同じターゲットに対してでも測定する度にわずかに異なった結果を返してきます。そのため1度の計測だけでは測定値を信頼できません。より信頼に足る測定値を得るには、測定を何度も行い平均値をとる必要があります。

測定距離の平均化

　平均は言うまでも無いですがすべての測定値を足して測定回数で割ると求まります。もちろん100回とか500回など測定回数を決めて平均を求めても良いです。今回はちょっと別の切り口として、同じ条件でどんどん測定して、都度平均値を求めて行く方法を取ってみる事にします。こうすると平均値が安定するまで試行回数を増やし続ける事が出来ます。

　やり方は至極単純で、測定する度に測定値を足し込み、測定回数で割った平均値を返すようにします。これをするには直前までの測定値の合計と測定回数をバッファする必要があります。こういうのはクラス化するのが分かり良いです。

　という事で積算的な平均を求めるクラスをPythonで作ります：

# データを追加して都度平均を求めるクラス

class ComulativeAverage:
    __total = 0.0     # データ積算値
    __count = 0       # データの個数

    # データを追加
    def add( self, data ):
        self.__total += data
        self.__count += 1
        return self.average()

    # 現在の平均値を取得
    def average( self ):
        return ( self.__total / self.__count, self.__count )
    
    # データをクリア
    def clear( self ):
        self.__total = 0.0
        self.__count = 0

内容についてはもう見ればわかるレベルに簡単なので説明は割愛します。このコードをaverage.pyとして保存し再利用します。

キャリブレーション距離関数

　この平均値算出クラスを使って実際にいくつかの真の距離に対する平均測定距離を出力してみました：

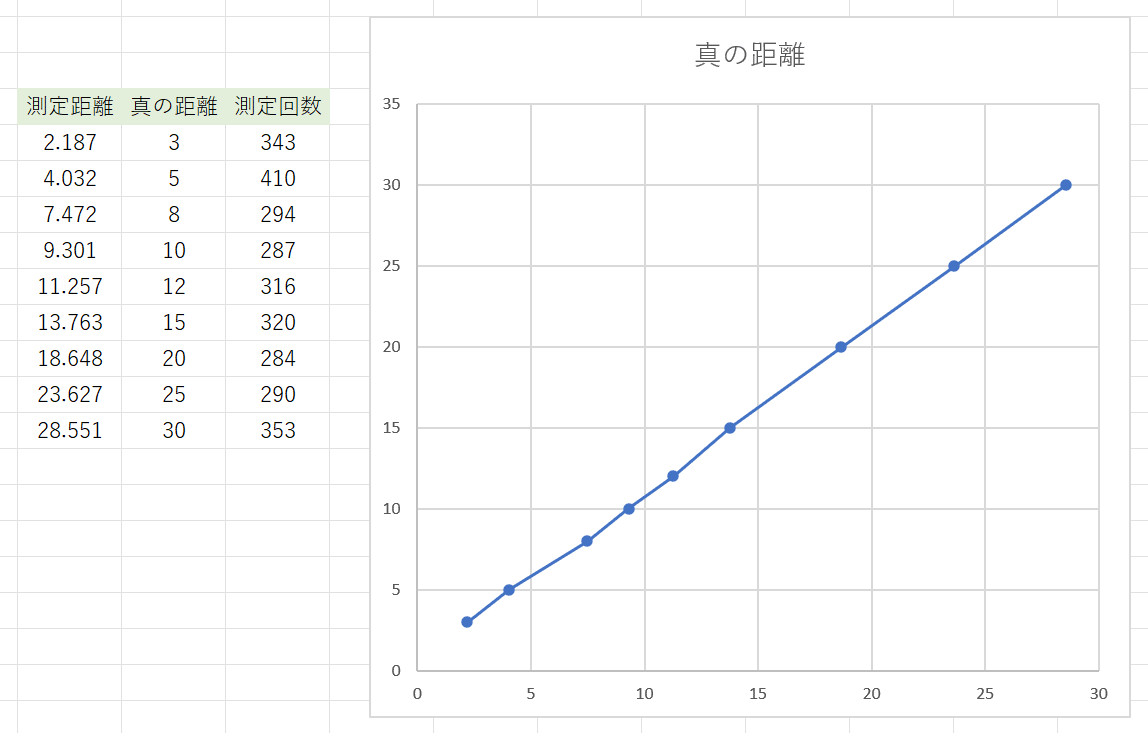
　横軸が測定距離、縦軸が真の距離です。比較的綺麗な直線関係になっていますが、10cm付近が若干ふらついている印象です。その辺りに機器の特性があるのかもしれませんね。横軸を測定距離にしているのは、キャリブレーションによって測定距離から真の距離を割り出す必要があるためです。

　このように測定距離と真の距離との関係を見い出したら、ここからキャリブレーション距離関数を作ります。これは色々な方法が考えられます。理想的なのは機器の測定可能範囲について細かくサンプリングして、上のようなグラフを表すデータを保持する事です。そうする事で任意の測定値に対して真の距離の推定値を近似的に求められます。

　理想的な方は実装が込み入るため、今回はもう少し簡易にしようかなと思います。測定値と真の距離の間に明瞭な直線関係があると仮定し、上のグラフに沿うような具体的な近似直線を求める事にしましょう。これはいわゆる「回帰分析」です。

回帰分析による直線のフィッティング

　線形回帰分析はそれ程難しく無いのでゴリゴリとコード書いても良いのですが、Pythonですから大概の物はあるんですね。もちろん回帰分析も例えばnumpyライブラリでサクッとできます。

　上のデータで測定距離をx、真の距離をyとした近似直線をnumpyで求めるコードは以下の通りです：

import numpy

# 回帰分析データ
#  x: 測定距離
#  y: 真の距離

xs = numpy.array([2.187, 4.032, 7.472, 9.301, 11.257, 13.763, 18.648, 23.627, 28.551])
ys = numpy.array([3.0, 5.0, 8.0, 10.0, 12.0, 15.0, 20.0, 25.0, 30.0])

coefs = numpy.polyfit( xs, ys, 1 )

print( coefs )

　numpy.polyfit関数はデータに対して多項式を当てはめる関数です。第1引数にX軸の値の配列、第2引数にY軸の値の配列を渡します。第3引数は最高次数で1にすると1次関数（直線）のフィッティングになります。

　上のコードを実行するとフィッティングした直線の係数が出力されます：

y=ax+bで、a=1.0309766、b=0.60897813のようです。実際グラフを重ねてみました：

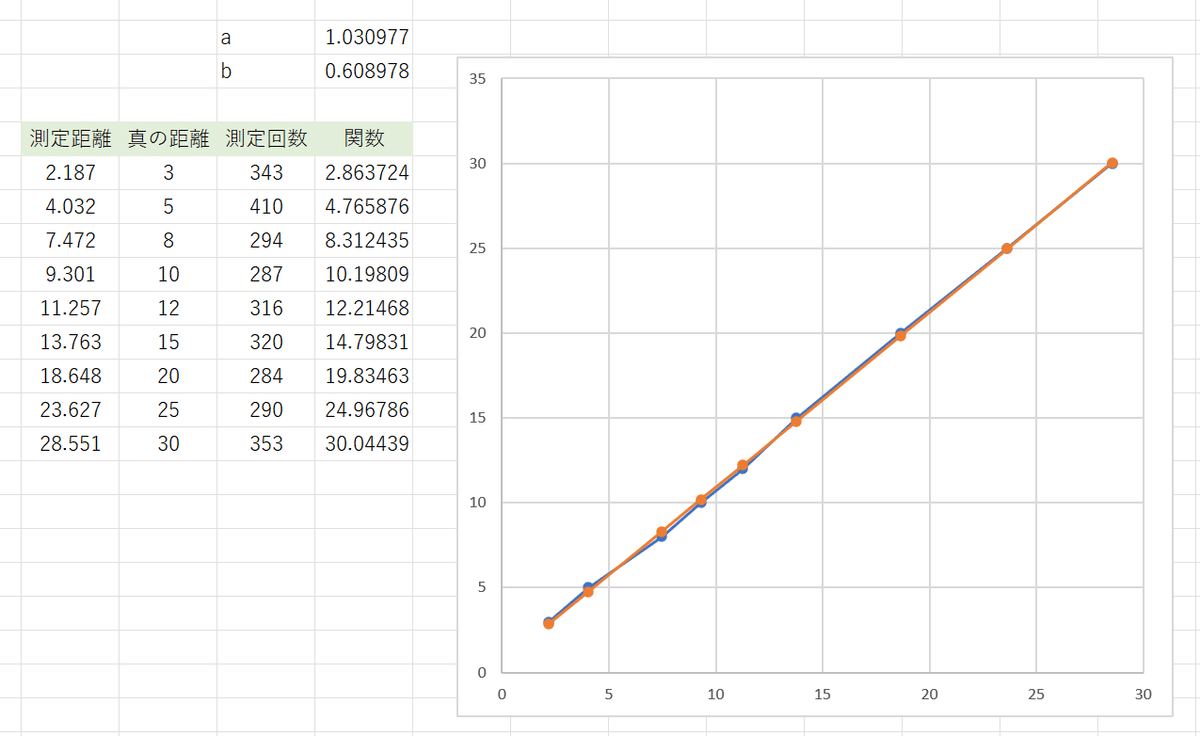
　上表の[関数]の列が距離センサーの測定値に対するキャリブレーション関数で求めた推定値です。2mmくらいズレていますが、まぁ簡易なので(^-^;。

キャリブレーション関数をコードへ

　このキャリブレーション関数を前回の距離センサーのコードに追加します：

def calcCaribDist( mesuredDist ):
    a = 1.0309766
    b = 0.60897813
    return mesuredDist * a + b


#距離を測定し続けてLCDに出力
while True:
    try:
        distCm = mesureDist()
        if distCm > 0.0:
            distCm = calcCaribDist( distCm )
            lcd.print( 0, 0, "DIST:" + "{:.3f}".format(distCm) + " cm     " )

    except KeyboardInterrupt:
        GPIO.cleanup()

　上は変更箇所だけ抜粋しています。変更前の元コードの全容は前回の記事をご参照下さい：

　mesureDist関数を呼ぶ事で距離センサーが1回測定を行い、概算的な測定距離をcm単位で返します。calcCaribDist関数にそれを渡すと、先の概算距離から推定距離を算出します。

　実際に測定してみたのがこちら：

　多少ずれはあるものの、それなりに近しい距離を出してくれているようです。

測定前にはキャリブレーションが必須

　良い感じに近似的な距離を表示してくれるようになりましたが、この固定したキャリブレーション関数で安定かというとNoです。

　超音波式の距離センサーは音速を使用しています。音速は温度や湿度、高度など外的要因により速度が変わってしまう為、同じ対象を同じ距離で測定してもセンサーが返す時間が微妙に変わってきます。キャリブレーション関数は「ある特定の環境で測定したデータ」を元に算出したので、別環境だとキャリブレーションがズレてしまうんですね。その為、測定前には都度キャリブレーションする必要があります。

　そういう理由から、距離センサーを扱うアプリケーションには「キャリブレーションモード」を設けないといけません。そのモードにしたら、ある真の距離（Dtrue）に対応した対象物を測定し(Dm, Dture)のデータセットを内部に保持します。これをアプリケーション側で沢山指示して、現環境に合うキャリブレーション関数をランタイムで作り直すんです。

　キャリブレーション後に、真の距離が分かっているターゲットを実測モードで再度測定し、望む距離が算出されていればOK。これで初めて距離センサーをその環境で使えるようになります。

終わりに

　今回は距離センサーのキャリブレーションについてあれこれ見て来ました。距離センサーが実は距離を測定していないという事から、変換補正の必要性が生じるわけで、キャリブレーションは必須なんですね。

　キャリブレーション関数として線形関数は流石に粗すぎます。実際はサンプリング点の傾向を加味した多次元関数やスプライン的な部分関数などを用いるのが一般的かなと思います。

　さて次回ですが、別の距離センサーが手に入りましたので、それを試してみます。ではまた(^-^)/