
勘違いしているかもしれない「一筆書き」
結論
「一筆書き」は大まかに分けて2種類ある
片方は解き方が簡単で、もう一方は難しい一筆書きである
難しい一筆書きの一般的な解法は未解決問題
「Fill」のルール
一筆書きパズル「Fill」のルールを言語化するとおよそ次のようなものよ。
一筆書きの開始位置は決まっている
筆は、上下左右のマスに移動できる
一度経過したマスには、二度踏むことができない
すべてのマスを踏めばOK
例

赤い点から縦横に移動して、全部のマスを一度ずつ踏むことができる?
例の解答

たしかに、すべてのマスを一度ずつといわれると「一筆書き」だけれども、みなさんが「一筆書き」と言われたら、次のような図じゃない?
一筆書きといえば

筆を離さずに、同じ線を通らずに書くことができるか、というパズルね。一筆書きと言われたら、こちらを思い浮かべる方が多いんじゃないかしら。
一筆書きができるかどうかをすぐに判定する方法は、多くの方がご存じかもしれないわね。
交差点に入る線の数に注目することね。スタート地点は「出」の線が1本で、ゴールは「入」の線が1本、そのほかの点では「入」と「出」が同じ数だけある必要があるわ。
だから、道中の交差点はすべて、偶数本の線につながっている必要があり、奇数だけ線が交わっているような交差点を出発および終点とすればよい。奇数だけ線が交わっているような交差点が3つ以上あると、一筆で書けないということがわかるわ。
この証明方法は、数学史上もっとも有名な人物の一人、レオンハルト・オイラーに発見されたのよ。
この方法なら、どんな図形が来ても、一筆書きできるかどうかが簡単にわかりそうだね!
二種類の一筆書き
これを、最初の「Fill」の例題について考えてみましょうか。上下左右に隣接するマスに移動できるということから、次のように点と線で表現することができるわ!

では、奇数本の線が入っている交差点はいくつでしょうね……
8個……
おかしいですね、これでは今の方法では「一筆書きが不可能」ということになっちゃう。けれど最初に見せた通り、一筆書きの解法は見つかっていたわ!!
てか、そもそも前提が違うのよ。一筆にする対象が違うわけ。
Fillでは別に、経路というか、線をすべて通る必要はなくて、点をすべて通ればよいの!!
オイラーさんが証明した方法は線の一筆書きに対する解法で、Fillは点の一筆書きだから、関係ないのよ!
点の一筆書きの解法?
じゃあ、このパズルをどうやって解いていくか、見ていきましょう!
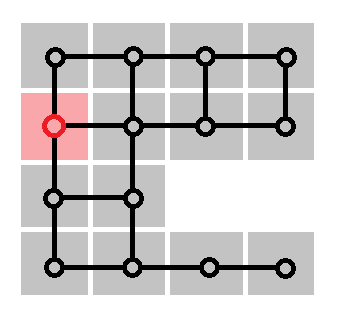
出発点は赤と決まっているから、終点を考えてみよっか!
と意気込みは入れたけれど、これは右下の行き止まりで決定ね。行き止まりは入ったら出られないから。もし行き止まりが複数あったら解がないわ。

その左のマスも、出る方向が決まっているから、もう片方の線から入ってくるわね。

出発点と終点以外は、入ってくる線と出ていく線の二本が必要だから、点に2本入っているところは2本とも経路に含まれるわね。

右上の4マスに注目して。青い線を経路に入れるとすると、経路が小さなループになってしまうから、経路に入れちゃだめね。

そうそう、出発点から出る経路は1本だけだから、出発点につながっている線はどれも経路にはなりえないわ。

こんな感じで、「経路に含まれることが確定した線(赤)」と、「経路に含まれないことが確定した線(青)」が順々にわかっていけば、一筆書きの経路は1通りに決まるね!
点の一筆書きの一般的な解法
今回の例では「点の一筆書き」ができることがわかったけれど、1マスごとに判定していたから、時間がかかったわね。「線の一筆書き」みたいに、効率よく求める方法はないかしら?残念だけれど、今のところ見つかっていないらしいわ。
------
そろそろ「数学」っぽさを出していきましょうか。
点と線で表現された図を離散数学の用語でグラフといいます(棒グラフのグラフとは、意味が違います)。点を線でつなげていればグラフなので、今回のパズルだけでなく、樹形図や路線図、ネットワークなど様々な場所で顔を出しています。
グラフ上で「線の一筆書き」の経路をオイラーパス、「点の一筆書き」の経路をハミルトンパス(あるいはハミルトニアンパス)といいます。
ハミルトンパスの出発点と終点が隣り合うとき、それらをつなげる線をハミルトンパスに加えると、すべての点を一度ずつ通る大きなループになります。このループをハミルトン閉路といいます(同様にオイラー閉路 or オイラー回路という言葉があります)。
任意のグラフに対し、そのオイラーパスの存在を証明するには先ほどの解説通りすぐできるのですが、ハミルトン閉路およびハミルトンパスが存在するかどうか(ハミルトン閉路問題)をすぐに判定する方法は現在未解決問題となっています。ハミルトン閉路問題、ハミルトンパス問題はNP完全という性質を持ち、解くことが難しいことが証明されています。さらに、グラフが「Fill」のようにグリッド(格子)の形をしている場合でも、NP完全であることが証明されています。
参考論文
A. Itai, C. H. Papadimitriou, and J. L. Szwarcfiter, Hamilton Paths in Grid Graphs. SIAM Vol. 11, Issue 4 • November (1982) 676-686.
S. Cook, The complexity of theorem proving procedures. Proceedings of the Third Annual ACM Symposium on Theory of Computing
(1971) 151-158.
L. A. Levin, Universal sequential search problems. Probl. Peredachi Inf. 9 (1973) 115-116.
