チェインと先読み
本記事は裏ペンシルパズル Advent Calendar 2022の13日目です。
元々は表の記事だったのですが追加の記事の方が内容的にとっつきやすいと判断し、めでたく裏送りとなりました。本記事のテーマはチェインと先読みのお話です。
1. 問題
本題に入る前に問題を2つ出します。
問1. 以下はへやわけの途中盤面の一部です。この状況のみから確定できる箇所がまだあります。どこでしょう?(答えはすぐ下)

問2. 問1の確定を人に説明するとき、あなたはどのような論理の流れで説明しますか?(答えは後ほど)
論理の流れと言うと曖昧ですが、例えばどこどこを仮定するとこう決まってこう結論が得られるというような具体的な結論を得る手順を一つ思い浮かべてください。
〜問1の解答〜
図の☆のマスが白マスに確定します。

これは以下のようなチェインによって説明できます。
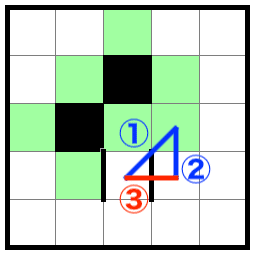
②隣接禁による弱リンク
③三連禁による強リンク
余談ですがチェインが三角形になるので、私はこの形の確定を勝手に三角手筋と呼んでいます。
2. で、結局チェインって何なの?
表の記事はもともとここの一章だったのですが、よく考えたらチェインに慣れ親しんでもらいたいという意図で書くチェイン解説記事は本記事とは別にまとめた方が良いと思い、記事を分けました。(そしてこの記事が裏に追いやられました。)
記事はこちらです。
上の記事では触れるのを避けましたが、より幅広いパズルにチェインを応用するならば、強と弱以外のリンクも考えた方が面白いのではないかと考えています。それについても色々書いていたのですが流石に時間が足りず、いつか完成した際にここに追記する予定です。
3. 単純仮定、いずれにしても、チェイン
3.1 単純仮定といずれにしても理論
さて、本題のチェインと先読みのお話。最初のへやわけの例を再掲します。

問2. 問1の確定を人に説明するとき、あなたはどのような論理の流れで説明しますか?
〜問2の解答例〜

さすがにチェインの説明を全てする必要はないでしょう。この確定を説明するだけならわざわざチェインなんて持ち出さなくとも
(1)Aのマスが黒マスになると仮定する。この時、BとCのマスは白マスとなり三連禁に反する。よってAは白マス。
とか
(2)三連禁によりBかCの一方は黒マス。いずれにしてもAは白マス。
でいいわけです。(上記は一例です。他にも考えられます。)
(1)はいわゆる単純仮定と呼ばれるものです。私は単純仮定がどこまでを指すのか未だによくわかっていないのですが、確定の逆を仮定して比較的軽い先読みでその破綻が導けるものの総称というイメージです。
(2)はいずれにしても理論と呼ばれます。 (いずれにせよ理論とかどちらにせよ理論とかどっちにしても理論とか呼ばれたりもします。元はニコリでLocked Candidatesに相当する手筋「いずれにしても理論」だと思われます。)
ある箇所の択(2択でなくても良い)に注目し、その場合分け全てに共通する確定を取り出す方法です。これも基本的にはそれぞれの場合について軽い先読みで共通項にたどり着ける場合を考えることが多いです。
チェインに関して(私がチェインをいちいち持ち出すせいで)よく言われるのが「結局上述のような軽い先読みで良いのではないか。」という意見です。それに対する私の主張を簡潔に言えば「良いと思います。そもそも何が違うんですか。」です。
3.2 同一性
チェインと単純仮定、いずれにしてもが大体同じであるということを言いたいのですが、そもそも“同じ”というのが何を指すのかを明確にしなければなりません。
去年の記事で論理を明確に記述する道具を用意したのでそれを元にチェイン(C)と単純仮定(1)、いずれにしても(2)を記述すると次のような形が自然かと思います。
$${(\{A,B,C\},R)\to(\{A,B,C\},R\cup\{\neg A\})}$$
(C)$${R=\{\neg A \lor\neg B,\neg A\lor\neg C,B\lor C \}}$$
(1)$${R=\{A\to\neg B,A\to\neg C,\neg(\neg B\land\neg C)\}}$$
(2)$${R=\{B\to\neg A,C\to\neg A,B\lor C\}}$$
こう見ると、全く同じというには無理がありそうです。ただ共通している点として、これらの制約は共に3つのパーツからなり、それぞれは同値であるという点です。そしてそのパーツは分断禁$${\neg(A\land B)}$$、隣接禁$${\neg(A\land C)}$$、三連禁$${\neg(\neg B\land\neg C)}$$とそれぞれ同値です。
一般に同値な制約を全て同じものとみなすことはできません。それをすると推論の全てのステップが同じものになってしまうので、解く過程を表すという本来の目的が失われます。むしろどのような制約同士が同値であってそれがパズルにどのように現れるか、というのはこの表現の考察対象です。
ただ、上で現れる2要素間制約の同値な言い換えは普段から無意識に行われており、その省略はしても良いでしょう。例えば隣接禁$${\neg(A\land B)}$$は実際には片方が黒マスならもう片方は白マス$${A\to\neg B}$$としてよく使われますが、これですら言い換えと見ることができます。
この2要素間制約の変換を自明な推論として無視することを許容すれば、(C),(1),(2)は同一視できます。
3.3 チェインの特徴
上で見たようにチェイン、単純仮定、いずれにしてもはある意味ではほとんど同じものと言えますが、もちろん全く同じものとは言えません。それらがどのように異なり、その中でチェインという形式を採用するメリットを考えます。
拡張も含めるとチェインにも色々ありますが、ここでは最も基本的なものに絞って考えます。「2要素間の制約(リンク)を直列に繋いだもの」をチェインと呼びます。
◯定義の明確さ
単純仮定、いずれにしてもと比較して、チェインは用語として表す範囲が明確です。私の知る限り単純仮定やいずれにしてもと仮定の境界は曖昧ですが、チェインの定義にリンクの長さや見つけにくさによる制限はなく、実用性とは切り離されて明確に定まっています。
◯前提の明確さ
推論過程としてチェインを使う際には、構成するリンクを明確にする必要があります。つまり、結論を得るための前提を過不足なく提示できます。例えば上のへやわけの説明では、単純仮定やいずれにしてもでは分断禁、隣接禁が効いていることがチェインに比べてぼやけた印象になります(意図的にぼやけさせました)。また、前提が明確であれば、同様の性質を持つ部品による変形もイメージしやすくなります。これは回廊の1の強リンクを回収の強リンクで張り替えてみた例です。
◯分岐の禁止
単純仮定、いずれにしてもではあまり意識されませんが、基本形のチェインに分岐はありません。したがって非常に単純な先読みであってもチェインでは表現できない場合があります。ある意味でチェインは先読みの一分類とも言えると思います。
◯対称性
前提を明確にした単純仮定やいずれにしてもとチェインの比較という話ですが、チェインの制約の表し方は原則として選言$${\lor}$$を採用します。含意$${\to}$$を制約の表し方として利用するのは同値ではありますが、長さによらず対称性を維持できる点、表し方が一意に定まる点が選言$${\lor}$$の採用理由です。またCNF(連言標準形)を意識してというのもあります。
3.4 チェインのデメリット
チェインに慣れすぎてどうしても甘くなってしまうため、もし意見があればいただきたいです。
◯分かりづらい
それは本当にそう思います。私も解説等では「簡単な先読みによって」を使います。チェインを使うのは、理詰めとして厳密性が欲しい場合、2択の連鎖などチェインが実用的な場合、意図的にチェインを仕込んだ場合、などでしょうか。
◯簡単な分岐に対しても表現力を失う
これに関してはチェイン以外のものを新たに用意する必要があります。ネットとかどうでしょうか。解く上ではまず人間に扱えない代物ですけど、理論上の道具と割り切れば悪くないと思います。
◯簡単な手筋の複合にも弱い
チェインを使った説明を試みる際によくぶつかる問題です。仮定すると手筋から簡単に処理できるのに、チェインに直すのは面倒な場合があります。しかし、これはむしろ今後の考察対象であると考えています。
◯実用性との関連は薄い
定義が実用性と切り離されているということは、ときに人間に取り扱うことが困難なものも含まれうるということです。どうしてもそこは割り切った考察にならざるを得ません。
4. まとめ
以上、私がチェインと先読みの関係として普段ふわっと思っていることを言語化してみました。私の中でチェインは厳密性を重視した先読みの一形式であって、解くための道具というよりも先読みを分類考察するための道具というイメージでしょうか。先読みを仕込むための道具でもあります。これはあくまでチェインに対する私のイメージなので他の方のイメージもぜひ聞いてみたく思います。
5. 付録1 ルール解釈の問題
ここまでチェインについて長々と話してきたのですが、関連する話題としてルール解釈の話を少しします。
ここでいうルール解釈とは自然言語で記述されたルールをどのように制約集合に書き換えるかという問題です。
へやわけを例にとります。まずへやわけはルール要素が隣接禁、分断禁、三連禁、数字表出からなります。
隣接禁の解釈は全ての隣接するマス$${A,B}$$について$${\neg (A\land B)}$$で良いでしょう。このように$${\neg,\land,\lor,\to}$$で書かれる制約を論理式型の制約と呼ぶことにします。チェインは論理式型の制約に対する推論です。
一方、数字表出は論理式で書くのは自然ではありません。部屋の要素集合$${X}$$に対して黒マスが4つなら$${X=4}$$などと書きたくなります。三連禁についてはちょうど先日わんどさんの記事がありましたが、太線2つをまたぐ各部分について$${X\geq 1}$$と書きたくなります。等号を上限と下限に分解すればこれらは全て不等号型の制約とでも言えましょうか。
この2つはよくある制約の表し方ですから、その扱いを考察すれば多くのパズルに共通する道具になると思います。例えば最初に出したへやわけの例で不等号型制約の三連禁をしれっと論理式型の強リンクで書いたりとかそういった話です。
一方、この2つで表す方法が曖昧なルールについては、手筋の考察はまだまだ発展途上であると考えています。代表的なものは言わずもがな、分断禁です。
一つの表現は白マスが連結ですが、これを各マスの条件として自然に書き下す処理が必要ですし、それと具体的な利用例とのつながりを明確化する必要もあります。最初のへやわけの例では白マス連結性を、白マスには隣接する白マスがあると考えると$${\neg A\lor\neg B}$$として、黒マスがループにはならないと考えると$${\neg(A\land B)}$$として利用できますが、もともとのルール解釈との繋がりは不明瞭な気がします。
解釈の問題というと小ループ禁も同様で、最近は隘路の導入によってだいぶ仲良くなれたような気がしますが、これも元々のルール解釈とどういう関係にあるのか、他にも隘路のような便利な道具があるのか、ルール解釈が考える一つの切り口にならないでしょうか(期待)。
6. 付録2 考察のメモ
メモしておかないと忘れるので。
◯2要素間制約の同値変形を自明な推論としたが、普段利用する自明な推論とは他にどのようなものがあるか?
一つ例を挙げるならこういうやつです。無意識の意識化。
要素集合$${X_n=\{x_j\}^{n}_{j=1}}$$上の不等号型制約を$${X_n\geq 1}$$のように書き表すことにする。この時、$${(X_n,\{X_n\geq 1,\neg x_n\})\to(X_n,\{X_n\geq 1,\neg x_n,X_{n-1}\geq 1\})}$$は推論。
◯手筋との複合的な先読みはどのようにチェインに直されるか?
手筋のリンク化というアイデアがあります。簡単に言えば手筋は前提と結論が論理包含で結ばれたものですが、その前提の否定と結論の間には論理包含と選言の言い換えによりリンクを張ることができます。一例ですがALSという考え方はまさにLocked Set系の手筋をリンク化したものとみなせます。
◯分岐を含む先読みはどのような表現にすれば良いか?
HoDoKuにはネットという解法があります。ネットは分岐の数や深さに制限を設けなければ、基本手筋に絞った一段仮定と同程度の表現力を持つと思われます。基本手筋に絞ったと書きましたがALSなどを導入するほど仮定で考えた時に使える手筋が増えます。一段仮定の表現範囲は凄まじいので、基本的にはチェインとネットの間が主な考察対象になるでしょうか。
◯不等号型制約に対する汎用手筋は何があるか?
いわゆる分割充填法になる気がします。Fish系も極論言えば分割充填法です。以下に一例を載せます。
要素集合$${X}$$の2つの分割$${\displaystyle\coprod^{n_1}_{j=1}X^{(1)}_j}$$と$${\displaystyle\coprod^{n_2}_{j=1}X^{(2)}_j}$$で、各分割上に制約
$$
\begin{align*}
&R^{(1)}=\{r^{(1)}_j\mid r^{(1)}_j=(X^{(1)}_j\leq M_j),1\leq j\leq n_1\}\\
&R^{(2)}=\{r^{(2)}_j\mid r^{(2)}_j=(X^{(2)}_j\geq m_j),1\leq j\leq n_2-1\}
\end{align*}
$$
がある。$${X^{(2)}_{n_2}}$$上の制約$${\displaystyle r=(X^{(2)}_{n_2}\leq d),d:=\sum^{n_1}_{j=1}M_j-\sum^{n_2-1}_{j=1}m_j}$$について、
$$
(X,R^{(1)}\cup R^{(2)})\to(X,R^{(1)}\cup R^{(2)}\cup \{r\})
$$
は推論。
