AtCoder精選良問「E - Come Back Quickly」Diff 1323

この記事はAtCoderの精選良問集マガジンの中の記事です。
私が良問だと思った問題を解説付きでまとめています。

AtCoder 精選良問集 Diff 茶後半～水前半｜Qlitre｜note

問題リンク

E - Come Back Quickly

問題概要

AtCoder 国にはN個の町とM本の道路が存在する。各道路は一方通行で、特定の町から別の町へと続いている。また、それぞれの道路を通るのに必要な時間も異なる。

問題：

• 各町から出発して、1本以上の道路を通りながら出発点の町に戻ってくるような経路を「正しい散歩経路」とする。

• すべての町について、正しい散歩経路が存在するかどうかを判定する必要がある。

• 正しい散歩経路が存在する場合、その経路で必要な最短の時間を計算する。

注意点として、

• 同じ町間に複数の道路が存在することもある。

• ある町から同じ町へと続く道路も存在する可能性がある。

考え方

まず、制約に目を向けると、NとMは最大で2000とけっこう小さい。最短距離というとダイクストラ法が思い浮かぶが、ある町からある町ではなくて、同じ町に戻ってくる最短距離、というのが難しいところ。

制約がそんなに大きくないので、思い切って超頂点を加えてみると意外とすっきりとする。

例えばN=3でこういうグラフがあったとする。

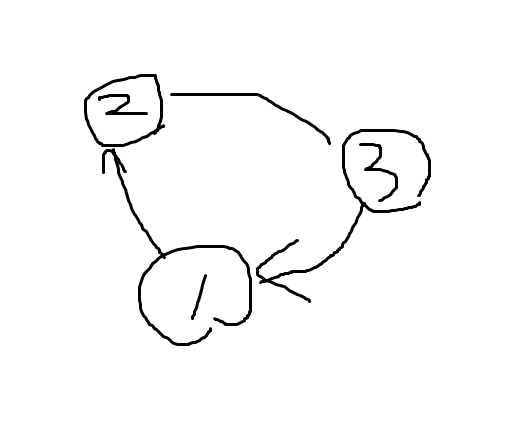
このときそれぞれの頂点に対して＋Nを加えた超頂点を考える。それで、遷移元の頂点から遷移先の超頂点、遷移元の超頂点から、遷移先の超頂点に辺をつなぐ。

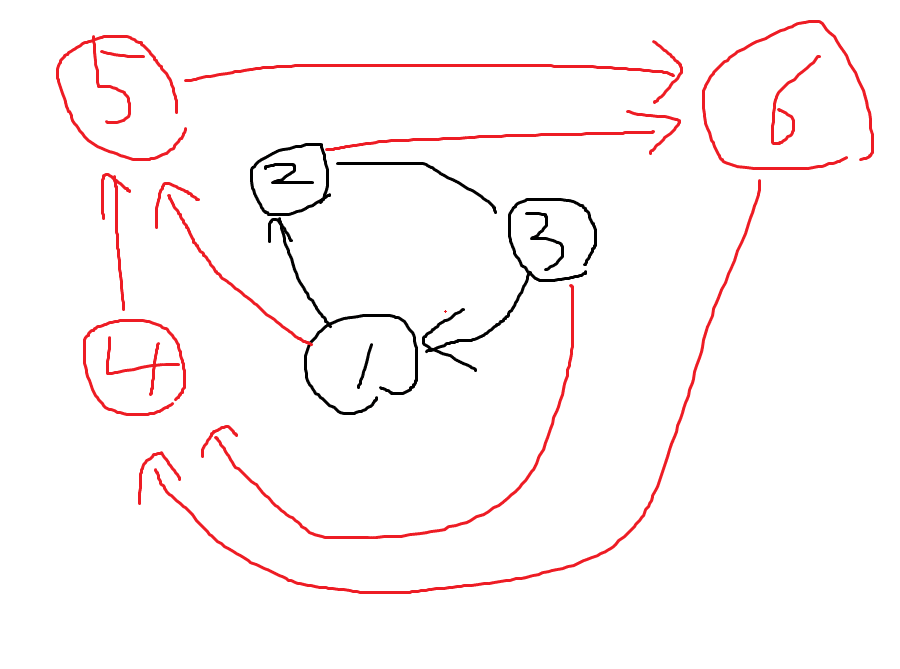
こういうイメージ。こうしておけば、例えば１→２→３→１と遷移する場合と、１→５→６→４と遷移する場合の距離は変わらない。ということは普通にダイクストラできるようになる。

あとは各頂点ごとにスタートの頂点から超頂点に対しての最短距離を求めていけば答えが出る。超頂点を加えたことで計算量は増えるが、元々の制約が小さいのでボトルネックにはならない。

実装

import { createInterface } from "readline";
import * as fs from "fs";
import { log } from "console";
import { exit } from "process";

export class BinaryHeap<T> {
    public heap: T[];
    private compare: (a: T, b: T) => number;

    constructor(compareFn: (a: T, b: T) => number) {
        this.heap = [];
        this.compare = compareFn;
    }

    public push(value: T): void {
        this.heap.push(value);
        this.bubbleUp(this.heap.length - 1);
    }

    public pop(): T | undefined {
        const last = this.heap.pop();
        if (this.heap.length > 0) {
            const result = this.heap[0];
            this.heap[0] = last!;
            this.sinkDown(0);
            return result;
        } else {
            return last;
        }
    }

    private bubbleUp(index: number): void {
        const element = this.heap[index];
        while (index > 0) {
            const parentIndex = Math.floor((index - 1) / 2);
            const parent = this.heap[parentIndex];
            if (this.compare(element, parent) >= 0) {
                break;
            }
            this.heap[index] = parent;
            this.heap[parentIndex] = element;
            index = parentIndex;
        }
    }

    private sinkDown(index: number): void {
        const element = this.heap[index];
        const length = this.heap.length;
        while (true) {
            const leftChildIndex = 2 * index + 1;
            const rightChildIndex = 2 * index + 2;
            let leftChild: T, rightChild: T;
            let swapIndex = null;
            if (leftChildIndex < length) {
                leftChild = this.heap[leftChildIndex];
                if (this.compare(leftChild, element) < 0) {
                    swapIndex = leftChildIndex;
                }
            }
            if (rightChildIndex < length) {
                rightChild = this.heap[rightChildIndex];
                if ((swapIndex === null && this.compare(rightChild, element) < 0) ||
                    (swapIndex !== null && this.compare(rightChild, leftChild!) < 0)) {
                    swapIndex = rightChildIndex;
                }
            }
            if (swapIndex === null) {
                break;
            }
            this.heap[index] = this.heap[swapIndex];
            this.heap[swapIndex] = element;
            index = swapIndex;
        }
    }

    public size(): number {
        return this.heap.length;
    }
}

function main() {
    const [n, m] = nextNums(2);
    const graph: Record<number, number[][]> = {};
    for (let i = 0; i < m; ++i) {
        const [a, b, c] = nextNums(3);
        const superA = a + n;
        const superB = b + n;
        if (!graph[a]) graph[a] = [];
        if (!graph[superA]) graph[superA] = [];
        // aからbへのコストcの辺を張る
        graph[a].push([b, c]);
        // aの超頂点からbへのコストcの辺を張る
        graph[superA].push([superB, c]);
        // aからbの超頂点へのコストcの辺を張る
        graph[a].push([superB, c]);
    }
    const inf = 10 ** 10;
    for (let i = 1; i <= n; i++) {
        // heapを初期化
        const heapq = new BinaryHeap<number[]>((a, b) => a[0] - b[0]);
        // 訪れた頂点の管理
        const vis: Set<number> = new Set();
        // 距離の初期化
        const distances: number[] = new Array(2 * n + 100).fill(inf);
        heapq.push([0, i]);
        // ダイクストラ法で最短距離を更新していく
        while (heapq.size() > 0) {
            const [dist, node] = heapq.pop()!;
            // 訪問済みだったらスキップ
            if (vis.has(node)) continue;
            vis.add(node);
            if (!graph[node]) continue;

            for (const [nextNode, nextDist] of graph[node]) {
                // 距離を更新していく
                const newDist = dist + nextDist;
                if (newDist < distances[nextNode]) {
                    distances[nextNode] = newDist;
                    heapq.push([newDist, nextNode]);
                }
            }
        }
        // iからi+nへの最短距離が戻った場合の最短距離
        const ans = distances[i + n];
        if (ans === inf) {
            log(-1);
        } else {
            log(ans);
        }
    }
}

let inputs = "";
let inputArray: string[];
let currentIndex = 0;

function next() {
    return inputArray[currentIndex++];
}
function nextNum() {
    return +next();
}
function nextBigInt() {
    return BigInt(next());
}
function nexts(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = next();
    return arr;
}
function nextNums(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = nextNum();
    return arr;
}
function nextBigInts(length: number) {
    const arr = [];
    for (let i = 0; i < length; ++i) arr[i] = nextBigInt();
    return arr;
}

// デバッグ環境がWindowsであれば条件分岐する
if (process.env.OS == "Windows_NT") {
    const stream = createInterface({
        input: process.stdin,
        output: process.stdout,
    });
    stream.on("line", (line) => {
        inputs += line;
        inputs += "\n";
    });
    stream.on("close", () => {
        inputArray = inputs.split(/\s/);
        main();
    });
} else {
    inputs = fs.readFileSync("/dev/stdin", "utf8");
    inputArray = inputs.split(/\s/);
    main();
}