相加相乗平均と関数の最大最小
問題
$${x\geqq 2,y\geqq1,\log_{2}{x^2y}=64}$$とする.このとき,$${(\log_{2}{x})(\log_{2}{y})}$$の最大値,最小値を求めよ.
解法
1.2次関数の最大・最小の問題として考える
$${x^2y=64}$$より,$${y=\frac{64}{x^2}}$$.
$${y\geqq1}$$より,
$$
\begin{align*}
\dfrac{64}{x^2} & \geqq 1\\
64 & \geqq x^2\\
\therefore 8 & \geqq x \geqq -8
\end{align*}
$$
$${x\geqq 2}$$とあわせて,$${8\geqq x \geqq 2}$$.
$${t=\log_{2}{x}}$$とおくと, $${3\geqq t \geqq 1}$$.
さらに,
$$
\begin{align*}
(\log_{2}{x})(\log_{2}{y})^2
&=6\log_{2}{x}-2(\log_{2}{x})^2\\
&=6t-2t^2\\
&=-2(t^2-3t)\\
&=-2\left(t-\dfrac{3}{2}\right)^2+\dfrac{9}{2}
\end{align*}
$$
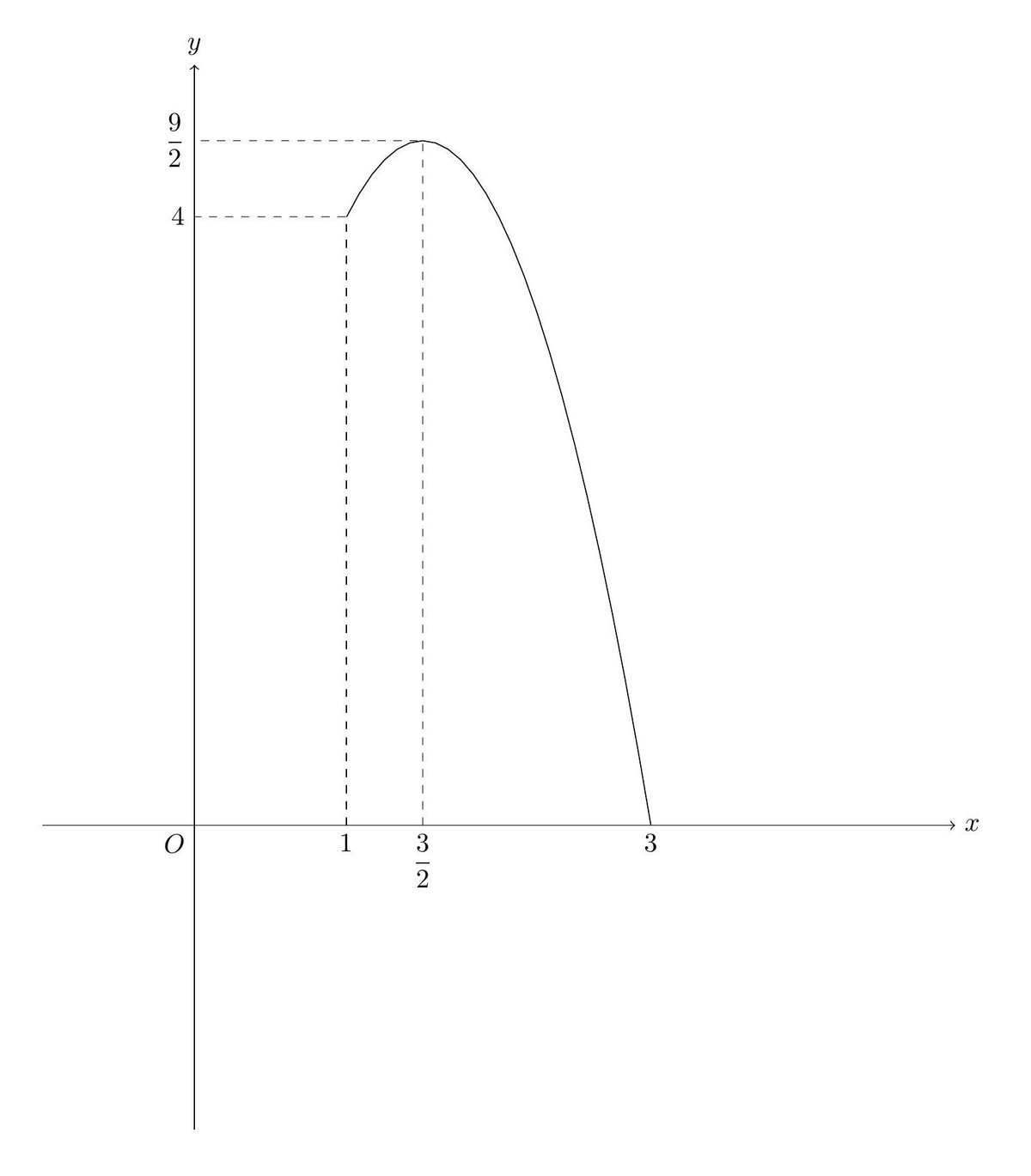
図より,$${t=\dfrac{3}{2}}$$,つまり$${x=2^{3/2}=2\sqrt{2}}$$のとき,最大値$${\dfrac{9}{2}}$$,$${t=3}$$,つまり$${x=2^{3}=8}$$のとき,最小値$${0}$$をとる.
2.相加相乗平均の大小関係を利用する
$${x=\log_{2}{x}}$$,$${\log_{2}{y}}$$とすると,$${x\geqq2}$$,$${y\geqq1}$$より,$${s\geqq1}$$,$${t\geqq0}$$.\\
よって,
$$
\begin{align*}
st \geqq 1 \cdot 0=0 \tag{1}
\end{align*}
$$
$${x^2y=64}$$より,
$$
\begin{align}
\log_{2}{x^2y}&=\log_{2}{64} \\
\log_{2}{x^2}+\log_{2}{y}&=\log_{2}{s^6} \\
2\log_{2}{x}+\log_{2}{y}&=6 \\
2s+t&=6 \tag{2}
\end{align}
$$
相加相乗平均の大小関係より,
$$
\begin{align*}
\dfrac{2s+t}{2} &\geqq \sqrt{2st}\\
\dfrac{6}{2} &\geqq \sqrt{2st}\\
3 &\geqq \sqrt{2st}
\end{align*}
$$
両辺を2乗して
$$
\begin{align}
9 & \geqq 2st \\
\dfrac{9}{2} & \geqq st \tag{3}
\end{align}
$$
(1),(3)より,
$$
\begin{align*}
\dfrac{9}{2} \geqq st \geqq 0
\end{align*}
$$
左側の等号が成り立つのは$${2s=t}$$のとき.(2)と連立して解くと,
$${s=\dfrac{3}{2}}$$,$${t=\dfrac{3}{4}}$$,つまり,$${x=2\sqrt{2}}$$,$${y=8}$$のとき.
よって,$${x=2\sqrt{2}}$$,$${y=8}$$のとき,最大値$${\dfrac{9}{2}}$$をとる.
右側の等号が成り立つのは$${t=0}$$のとき,このとき,(2)より,$${s=3}$$.
よって,$${x=8}$$,$${y=1}$$のとき,最小値$${0}$$をとる.
3.2次方程式の解の存在範囲の問題として考える
$${x=\log_{2}{x}}$$,$${\log_{2}{y}}$$とすると,$${x\geqq2}$$,$${y\geqq1}$$より,$${s\geqq1}$$,$${t\geqq0}$$.
$${x^2y=64}$$より,
$$
\begin{align}
\log_{2}{x^2y}&=\log_{2}{64} \\
\log_{2}{x^2}+\log_{2}{y}&=\log_{2}{s^6} \\
2\log_{2}{x}+\log_{2}{y}&=6 \\
2s+t&=6 \tag{4}
\end{align}
$$
ここで$${st=k}$$とすると,$${s}$$,$${t}$$は$${z}$$の2次方程式
$$
\begin{align*}
z^2-6z+2k=0 \tag{4}
\end{align*}
$$
の解である.いま$${s\geqq 1}$$,$${t\geqq 0}$$だから,$${z}$$の2次方程式(4)は0以上の解と2以上の解を1つずつもたなければならない.このとき,2次方程式(4)の判別式を$${D}$$とすると,
$$
\begin{align*}
\dfrac{D}{4}=3^2-2k=9-2k
\end{align*}
$$
であり,
$$
\begin{align*}
\dfrac{D}{4}\geqq 0 かつ 2k \geqq 0
\end{align*}
$$
が成り立たなければならない.これを解いて,$${\dfrac{9}{2}\geqq k \geqq 0}$$.
$${k=\dfrac{9}{2}}$$のとき,2次方程式(4)の解は
$$
\begin{align*}
z=-\dfrac{-6}{2}=3
\end{align*}
$$
よって,$${2s=t=3}$$.$${s=2^x}$$,$${t=2^y}$$より,$${x=2\sqrt{2}}$$,$${y=8}$$
$${k=0}$$のとき,$${z=0,6}$$.$${2s\geqq 2}$$,$${t\geqq 0}$$より,$${2s=6}$$,$${t=0}$$,つまり$${x=8}$$,$${y=1}$$のとき.
$${x=2\sqrt{2}}$$,$${y=8}$$のとき,最大値$${\dfrac{9}{2}}$$
$${x=8}$$,$${y=1}$$のとき,最小値$${0}$$
