【レポートの書き方講座】 #4 標準不確かさについて学ぼう！【無料で読めます】

　こんにちは！今回も頑張っていきましょう！
　前回までは基本的に$${\LaTeX}$$の扱い方について学んできましたが，今回はどちらかというと「新しい概念」について学びます．それではいってみよ〜！

箇条書き

　まず，前回取り上げなかった「箇条書き」についてです．まず代表的なのがこれ．自分でコピペして実行してみましょう！

\begin{itemize}
\item あいうえお
\item かきくけこ
\end{itemize}

こんな感じで，\begin{itemize}〜\end{itemize}環境の中で，それぞれの要素を\itemを使って表します．入れ子にすることもできます．

\begin{itemize}
\item あいうえお
\item かきくけこ\begin{itemize}
\item がぎぐげご
\end{itemize}
\end{itemize}

次に，もう少し便利な箇条書きです．先ほどの箇条書きを，次のように書き換えてみましょう

\begin{enumerate}
\item あいうえお
\item かきくけこ
\end{enumerate}

こうなったと思います．このように，enumerateを使うと数字で箇条書きを行うことが出来ます．

数字で箇条書きができる，ということは，\labelを使って数字を抽出することもできそうです．やってみましょう！

\begin{enumerate}
	\item あいうえお\label{あいうえお}
	\item かきくけこは\ref{あいうえお}である．
\end{enumerate}

できましたね！
入れ子ももちろん扱うことが出来ます（ここでは割愛します）

数字の部分を，例えば(1)，(2)…などに変更したい場合は，次のように書きます．

\begin{enumerate}
	\renewcommand{\labelenumi}{(\arabic{enumi})}
	\item あいうえお\label{あいうえお}
	\item かきくけこは\ref{あいうえお}である．
\end{enumerate}

\renewcommandは「現在あるコマンドを作り替えてね」という意味です．\newcommandが「コマンドの定義」であったのに対し，\renewcommandは「コマンドの再定義」を表します．
ここでは\labelenumiというコマンドを変更していますが，これは「\label」「enum」「i」というように切って読んでみてください．\labelというのは「数字のラベル」のこと．enumはenumerateのことです．最後のiはなにかというと，enumerateを入れ子にしたときの深さを表します．入れ子なしのときは「i」，1回入れ子をした場合は「ii」，2回入れ子をした場合は「iii」を使って表します．
次の\arabicは「アラビア数字」と言う意味です．他にも\romanだと「ローマ数字（i，ii，iii，iv….）」，\Romanだと「大文字のローマ数字（I，II，III，IV……）」\alphだと「アルファベット」，\Alphだと「大文字のアルファベット」を指定することが出来ます．{}の中にある「enumi」は先ほど同様「enum」と「i」で分けて考えます．わかりづらいので，ここは例を示しておきます．

\begin{enumerate}
	\renewcommand{\labelenumi}{\Large\arabic{enumi}.}
	\item 関数$f(x) = 2\log{(1+e^x)}-x-\log{2}$を考える．
	\begin{enumerate}
		\renewcommand{\labelenumii}{(\arabic{enumii})}
		\item $f(x)$の第2次導関数を$f''(x)$とする．等式$\log{f''(x)}=-f(x)$が成り立つことを示せ．
		\item 定積分$\displaystyle \int_0^{\log{2}}(x - \log{2})e^{-f(x)}dx$を求めよ．
	\end{enumerate}
	\item 極限値$\displaystyle \lim_{n\rightarrow\infty}\int_0^{n\pi}{e^{-x}|\sin{nx|}dx}$を求めよ．
\end{enumerate}

さらに便利にしたいときには，プリアンブルに次のコマンドを書きましょう

\usepackage{enumerate}

すると，こんなふうに書くだけでさっきと同じものが書けます

\begin{enumerate}[(1)]
\item あいうえお
\item かきくけこ
\end{enumerate}

大抵の場合，enumerateパッケージを使ってしまえば簡単にかけるので，これを使うのが得策でしょう．

さて，$${\LaTeX}$$について一通り終わりました！お疲れ様でした！
次回かその次くらいで「参考文献の書き方」について書こうと思っています．そのときにまた$${\LaTeX}$$の新しいコマンドを学びますが，とりあえずひと段落したと思ってくれて大丈夫です！
ちょっと難しいので割愛しましたが，フォントとかに凝りまくるとこんな感じのやつも自分で作れるようになります！頑張ってね！
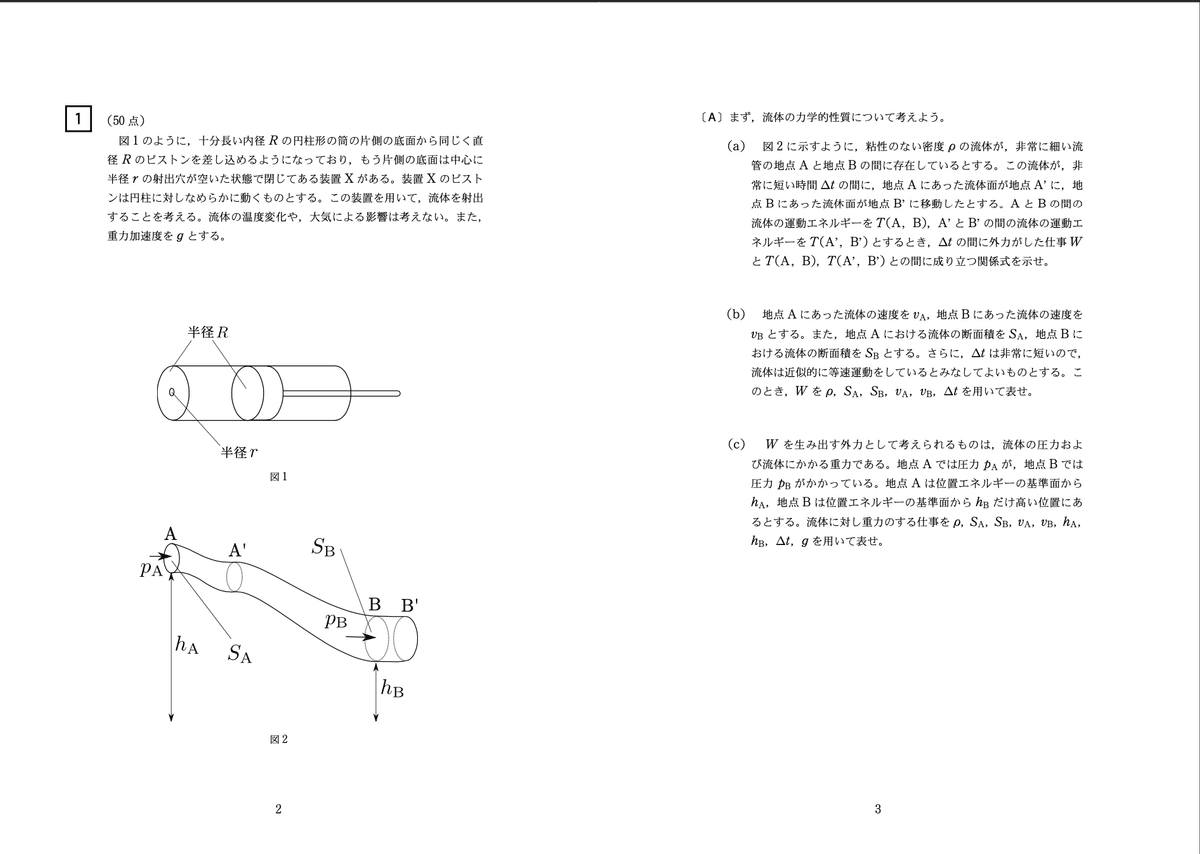
（ちなみにこの物理の問題は私のオリジナルです．解いてみたい人がいたら続きも送るのでDMかなんかしてねw）

不確かさとは

　さて，それでは1年生の関門，不確かさについて学んでいきましょう！！
　言うほど大して難しいものでもないので気楽にいきましょう〜

　不確かさ，というのは，測定値や実験値の曖昧さを表す言葉です．「誤差」という言葉も一緒に使われることがありますが，「誤差」が単なる測定値と真の値の差を表すのに対し，不確かさは実験値を統計的に処理することで「実験の大体のアタリをつける」ものです．といわれてもピンとこないと思うので，とりあえず基礎科学実験Aのテキストp6を開いてください．まあなんかうんにゃかうんにゃかっていろいろ書いてありますが，このあたり4ページで伝えたいことはズバリこれです．

実験って割とズレる！！！

高校までの実験では，誤差の原因こそ考えることはあっても，その誤差が「妥当なものなのかどうか」まできちんと検証することはありませんでした．大学からは，「ズレの原因が〇〇だと仮定すると文献値と比較してこのくらいズレるはずで，実際実験してみた結果もそうなってるからたぶんズレの原因は〇〇なんだろうな」という考察を結構しっかりと考える必要があります．その際に，まずは「その実験がどのくらい正確だったのか」を数値的に表さないことには考察ができません（理系ってそういう生き物なので）．逆に言えば，不確かさがわかることで，結構いろんなことが考察できてしまうのです！

不確かさの原因

まずは不確かさの原因について考えていきます．大きく分けてこんな感じ．

• 個人的要因：要するに実験がヘタクソってことです．読み間違いだったり，器具の読み方の癖だったりが影響します．

• 系統的要因：器具や機械にも読み取りの限界があります．また，物理では計算式をゴリゴリに近似するので，その近似による代償として多少ズレが生じることがあります．

• 偶然的要因：「まったく同じ環境」というのはどんなに頑張っても作り出せません．温度だったり，電磁波だったり，周りのさまざまな条件の変動，あるいは機械の不調や不安定さなどによりズレが生じることがあります．

標準不確かさとは

　前項でお話ししたズレというのは，何度も繰り返し実験を重ねるうちに分布が出来上がります．「ズレの大きさが小さいものほど多く，ズレの大きさが大きいものほど少なくなる」ということです．
　何言ってんだこいつ？と思うかも知れませんが，ちょっと立ち止まって考えてみてください．
　皆さんが一度は受けたであろう大学受験の模試．模試で一番多いのは偏差値50近辺の人たちです．逆に偏差値30だったり，偏差値70だったりといった人たちは，偏差値50帯に比べて少なかったと思います．偏差値20や80の人は滅多にいませんよね．このように考えると，ある程度の数のデータを集めたとき，「ズレの大きさが小さいものほど多く，ズレの大きさが大きいものほど少なくなる」という考え方がしっくりくるのではないでしょうか．

ここでよく出てくるのがGauss分布（正規分布）というやつです．模試の偏差値なんかはGauss分布をもとにして計算されています．数学Bで「確率分布と統計的な推測」を履修した人はわかるかもしれませんが（ちなみに私は履修していません……），こんな形のやつです．

　どこかしらでみたことはあると思います．
横軸は$${x-X}$$軸です．$${x}$$は実験データの値を，$${X}$$は後述しますが実験データの平均値を表しています．縦軸はそのデータが存在する確率を表していますが，簡単に言えばそのデータが出た個数です．皆さんが数学I「データの分析」で習ったヒストグラムのような感じのものだと思ってください．つまりこのグラフでは，$${x-X = 0}$$，すなわちデータの値が平均値に等しいところで最も多くのデータが観測されたことになります．

　この曲線の関数（確率関数といいます）はこんな感じになってますが，覚える必要はないです（縦軸を$${p(x)}$$とします）．

$$
\displaystyle p(x) = \frac{1}{\sqrt{2\pi} \sigma}\exp\left\{-\frac{1}{2}\left(\frac{x-X}{\sigma}\right)^2\right\}
$$

さて，こんな数式突然出されても意味わかりませんよね．少しずつ解説したいと思いますので，一旦Gauss分布の話は忘れてください．

　まず，$${X}$$は先ほども申し上げたように実験データの平均値です．想像つかないかも知れませんが，大学の実験では同じ値を複数回測ります．長さを測るにしても，質量を測るにしても，時間を測るにしても，複数回同じデータをとってその平均値を求めます．
　なぜこんなめんどいことをするのかというと，平均値は真の値に近いからです．専門用語で最確値といいます（証明は基礎科学実験Aのテキストp11にありますが，読まなくてもOK）．
　これは数学を使わなければ感覚的な問題になってしまうのですが，平均というのは簡単に言えば誤差をならしたものです．1つ1つの測定の誤差が相殺されるので，とりあえずデータをとれるだけとって平均値を求めればより真の値に近い値がでてくるっしょ！とこういう流れです．

　ただ，ここでひとつポイントがあります．平均値は真の値に「近い」だけで，「平均値＝真の値」ではありません．しかも，平均値が出たからといって，平均値がどのくらい真の値に近いか（つまりは実験の信憑性）まで計り取ることは出来ません．

　平均値がどのくらい真の値に近いかどうかは，データのばらつきで決まります．
データのばらつき……どこかで聞いたことあるような……
……………..
……………..
そうです．皆さんが数学Iで学習した標準偏差．もう名前も聞きたくないかも知れませんが，あの計算がむちゃむちゃめんどいアレです．大学からは，ちょっと式が変わってデータの個数$${N}$$ではなく$${N-1}$$で割ります．

$$
\displaystyle \sigma = \sqrt{\frac{1}{N-1}\sum_{k = 0}^{n}(x_k - X)^2}
$$

これを理解した上で，先ほどのグラフをもう一度みてみましょう．

$${x-X}$$軸に標準偏差$${\sigma}$$の姿がありますね．Gauss分布では，平均値の位置を$${0}$$としたとき，$${\pm\sigma}$$の位置にデータ全体の$${68.3\%}$$が，$${\pm2\sigma}$$の位置にデータ全体の$${95.5\%}$$が，$${\pm3\sigma}$$の位置にデータ全体の$${99.7\%}$$が含まれることが知られています．

　さて，今までは実験データと平均値について考えてきましたが，今度は「平均値と真の値の関係について」詳しくみていきましょう！
　先ほど申し上げたGauss分布ですが，不確かさを扱うときには「実験データを直接Gauss分布に当てはめる」ということはしません．不確かさを扱うときの手順はこんな感じです．

1. 実験によりとにかくデータを集める

2. 集めたデータの平均値$${\overline{X}}$$をとる

3. 平均値$${\overline{X}}$$は真の値$${\mu}$$に近い（Gauss分布による）．そこで，「真の値$${\mu}$$を『平均値の平均値』とみなしたときの平均値$${\overline{X}}$$の分布」をGauss分布に当てはめる

4. 3.から，$${\mu}$$のとりうる範囲を求める．これが標準不確かさ．

　さきほども述べたように，「平均値＝真の値」ではありません．実験によりデータを集めれば集めるほど平均値は真の値に近づくと考えられますが，それは「真の値に近づく」というだけで，本当に真の値を出したければ$${\infty}$$回実験を行わないといけないのです．それは時間的にも労力的にも不可能なので，学生実験ではせいぜい5回とか10回とかの実験データから真の値を推測する必要があります．このように，もともと大きな全体の集団（$${\infty}$$回の実験）があるうちの一部分（5回・10回の実験）だけを切り取ることで全体の推測をすることを標本調査といいます．全体の大きな集団のことを母集団（全体集合の統計学上の呼び方），切り取った一部分の集団のことを標本（部分集合の統計学上の呼び方）といいます．これに対し，母集団全体を調査することを全数調査といいます．

実は標準偏差の式が$${N-1}$$になっていたのは，
$${\displaystyle\sigma = \sqrt{\frac{1}{N}\sum_{k = 0}^{n}(x_k - X)^2} }$$

が全数調査の標準偏差であるのに対し，
$${\displaystyle\sigma = \sqrt{\frac{1}{N-1}\sum_{k = 0}^{n}(x_k - X)^2} }$$
が標本から求めた母集団の推定標準偏差であるためです．つまり求めているものが違います．厳密な証明は確率統計をきちんとやらなければ難しいですが，簡単な証明は基礎科学実験Aのテキストp12にあるので興味があれば読んでみてください．

　さて，先ほどの箇条書きに書かれていた$${\overline{X}}$$は標本の平均です．この平均のことを標本平均といいます．標本平均は，その「標本自体のばらつき」がありますから，真の値とは言えません．そこで，標本平均そのものの分布を考えます．
　目指すものは真の値ですが，Gauss分布に当てはめると，母集団の平均値は真の値に近いとみなすことができます．ここで「とにかくたくさんの標本平均を取らないといけないのでは？」と思うかも知れませんが，そんなことはありません．さきほど「とにかくたくさんデータを取った」のは，より確かな標本平均を得るためです．一度標本平均を求めてしまえば，あとはGauss分布の数式に当てはめるだけ！

　さて，$${n}$$回の測定により，次のような実験データが得られたとします．

$$
X_1, X_2, X_3,\cdots,X_n
$$

このとき，母集団の平均値，すなわち真の値が$${\mu}$$，母集団の分散が$${\sigma^2}$$であると仮定することにしましょう．このとき，$${X_1, X_2, X_3,\cdots, X_n}$$は，平均値$${\mu}$$，分散$${\sigma^2}$$の正規分布に従っていると考えることができます．

このとき，

$$
X_1 + X_2 + X_3 + \cdots + X_n
$$

は（証明は確率分布をもっときちんと学ばなければいけないので割愛しますが）平均値$${n\mu}$$，分散$${n\sigma^2}$$の正規分布に従うことが知られています．これを用いることで計算することにより，

$$
\displaystyle \overline{X} = \frac{X_1 + X_2 + X_3 + \cdots + X_n}{n}
$$

（標本平均ですね）は，（これまた証明を割愛しますが）平均値$${\mu}$$，分散$${\sigma^2/n}$$の正規分布に従うことが知られています．これをGauss分布の式に当てはめてみましょう．

$$
\displaystyle p(\overline{X}) = \frac{1}{\sqrt{2\pi} \dfrac{\sigma}{\sqrt{n}}}\exp\left\{-\frac{1}{2}\left(\frac{\overline{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}\right)^2\right\}
$$

ここでもう一度先ほどの図の出番です．

この図で$${x-X}$$だったところが$${\bar{X}-\mu}$$に，$${\sigma}$$だったところが今度は$${\displaystyle \frac{\sigma}{\sqrt{n}}}$$になります．

　さて，赤の範囲には全体の$${68.3\%}$$が含まれるのでした．つまり，$${68.3\%}$$の確率で

$$
\displaystyle -\frac{\sigma}{\sqrt{n}}\leq\bar{X}-\mu \leq \frac{\sigma}{\sqrt{n}}
$$

すなわち

$$
\displaystyle \overline{X} - \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} + \frac{\sigma}{\sqrt{n}}
$$

となることがわかります．こうして，真の値$${\mu}$$が$${68.3\%}$$の確率で

$$
\displaystyle \overline{X} - \frac{\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} + \frac{\sigma}{\sqrt{n}}
$$

の範囲にあることがわかりました．このようにして，ある確率$${\gamma}$$（今回は$${68.3\%}$$）で真の値$${\mu}$$が含まれるような範囲のことを信頼区間といいます．また，$${\gamma}$$は信頼度といいます．

　信頼度を$${95.5\%}$$とおけば，範囲は$${\pm2\times標準偏差}$$でしたから，

$$
\displaystyle -\frac{2\sigma}{\sqrt{n}}\leq\bar{X}-\mu \leq \frac{2\sigma}{\sqrt{n}}
$$

つまり信頼区間は

$$
\displaystyle \overline{X} - \frac{2\sigma}{\sqrt{n}} \leq \mu \leq \overline{X} + \frac{2\sigma}{\sqrt{n}}
$$

となります．このように，Gauss分布を元にしたときの信頼区間は，定数を$${c}$$として，

$$
\displaystyle \overline{X}\pm\frac{c\sigma}{\sqrt{n}}
$$

の範囲になりますが，この$${\displaystyle \frac{c\sigma}{\sqrt{n}}}$$のことを理科の世界では拡張不確かさといい，特に$${c = 1}$$の場合を標準不確かさといいます（というよりは，標準不確かさを拡張させて信頼度を自由に変更できるようにしたのが拡張不確かさです）．標準偏差を使った不確かさだから「標準不確かさ」です．また，係数$${c}$$のことを包含係数といいます．$${X}$$の不確かさのことを$${\Delta X}$$と表記します．つまり

$$
\displaystyle \overline{X}\pm\frac{c\sigma}{\sqrt{n}}　＝\overline{X}\pm\Delta \overline{X}
$$

です．
　特に実験で指示されていない場合は，拡張不確かさではなく標準不確かさを用いてください．

注：本来，母集団の分散が未知である場合はスチューデントの$${t}$$分布と呼ばれる分布を用いて計算します．計算手順自体が同じであること・基礎科学実験Aのテキストで触れられていないことから今回はGauss分布を使いましたが，II類に進む人は後期の確率統計の授業で扱いますのでなんとなく頭に入れておいてください．

　不確かさの有効数字は1桁で，繰上げ計算です．そして，不確かさが発生した桁を測定値の有効数字として扱います．例えば重力加速度の測定実験で，

$$
\overline{g} \;/\;\mathrm{m\;s^{-2}}=9.756234…，\Delta \overline{g} \;/\;\mathrm{m\;s^{-2}}= 0.00023145…
$$

という計算結果が出たときは

$$
g\;/\;\mathrm{m\;s^{-2}} = 9.7562 \pm 0.0003
$$

と表記します．

　今回は不確かさのうち最も基本的かつみんながつまづく「標準不確かさ」について解説しました．次回も不確かさの続きを解説します．

本日の課題

　あなたは，実験により次の重力加速度のデータを得ました．このデータより得られる重力加速度の値と標準不確かさを求めなさい．有効数字も考慮すること．Excelを用いてもよい．

1回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8123}$$
2回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.7921}$$
3回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8023}$$
4回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8099}$$
5回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8102}$$
6回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.7999}$$
7回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.7923}$$
8回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8015}$$
9回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.8012}$$
10回目：$${g\;/\;\mathrm{m\;s^{-2}} = 9.7922}$$

本日の課題の解答

$${g\;/\;\mathrm{m\;s^{-2}} = 9.801 \pm 0.003}$$

Pythonでのコーディング例です．プログラミングがわからなくても，コメントを読むことで流れがわかるようになっています．

'''本当はコメントには# を使いたいのですが，ハッシュタグの扱いになってしまうのでトリプルクオーテーションを使います（このまま実行できます）'''
'''mathモジュールをimportします'''
import math
'''データの配列を用意します'''
a = [9.8123, 9.7921, 9.8023, 9.8099, 9.8102, 9.7999, 9.7923, 9.8015, 9.8012, 9.7922]
'''xは平均を表します'''
x = 0
'''s2は分散を表します'''
s2 = 0
'''dxは不確かさを表します'''
dx = 0
'''まず平均値を求めるために，すべての測定値の和を出します'''
for i in a:
	x = x + i

'''和を10で割ることで平均値を出します'''
x = x / 10

'''求めた平均値を使って二乗和を出します．'''
for i in a:
	s2 = s2 + (i - x)**2

'''二乗和を(10-1)で割ることにより，分散を出します．'''
s2 = s2 / (10.0 - 1.0)

'''10で割ってから平方根を取ることにより，標準不確かさを出します．'''
dx = math.sqrt(s2 / 10)

'''それぞれ出力します．x = 9.80139，dx = 0.002416491947707261となるはずなので，dxは繰上げにより0.003となります．'''
'''これにより小数第三位に不確かさが発生したので，xの有効数字は小数第三位となります．ゆえに，x = 9.801です．'''

print(x)
print(dx)

これで今回の内容は終了です．10000字を超えてしまいました……
いいなと思っていただけたら投げ銭お願いします！