主成分分析 （PCA）

・主成分分析とは：多変量(多次元)の説明変数の次元数を減らす手法の一つ

・デメリット：情報の復元できない損失を伴う場合がある

・メリット：分析の効率化や多次元データの2次元可視化する　

・関連公式：

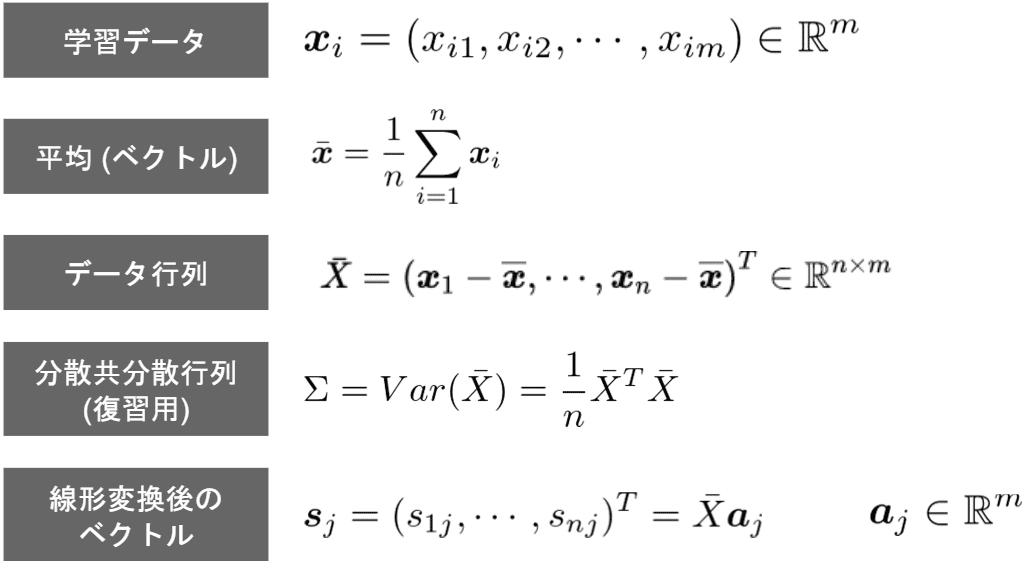
・変換の考え方：線形変換 x` = x・w(xはn次元、x`はｍ次元、m<n)において、線形変換後の変数x`の分散が最大となるようなw(size=(n,m))を求める。分散の大きさを圧縮の基準にする理由は圧縮したデータができるだけ互いに離れたほうが区別しやすい、つまり情報の損失が少ないと考えるため

・最適化問題の解き方：

・実際の手順：1)分散共分散行列Σを求める。2)Σ行列の固有値(λ)と固有ベクトルを求める。3)n番目の固有ベクトルが第n主成分の変換ベクトルである。

・例：

固有値は固有値 77.620と46.379、固有ベクトルx1=(0.940,0.340)、固有ベクトルはx2=(0.340,-0.940)。固有ベクトルx1.Tをかけると第一主成分変換になる。

・寄与率：第k主成分が持つデータ全体の情報量の割合

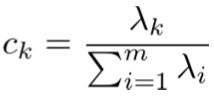
・累積寄与率：上記の累計

課題：(乳がん検査データ)31次元を2次元上に次元圧縮した際に、うまく判別できるかを確認→難しい

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_breast_cancer

x = load_breast_cancer().data
y = load_breast_cancer().target
xy = np.hstack([x,y.reshape(-1,1)])#xとy両方結合して可視化する
pca = PCA(n_components=2)
res = pca.fit_transform(xy)

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
x1,y1 = res[y==1][:,0],res[y==1][:,1]
x2,y2 = res[y==0][:,0],res[y==0][:,1]
ax.scatter(x1,y1, c='red')
ax.scatter(x2,y2, c='blue')
fig.show()

考察

・PCAでは情報の量を分散の大きさとして扱うことが必ずしもいい基準ではない

・PCAはある程度では単層ニューラルネットワークのautoEncoderに相当する

・可視化ツールとして使うことが多いが、現在のAI領域ではデータ圧縮に使われることが少なくなった