非線形回帰モデル

・非線形回帰問題：線形モデルでは十分にフィッティングできない問題

・基底展開法：回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用し、パラメータは最小2乗法や最尤法により推定する。よく使われる基底関数、項式関数、ガウス型基底関数、スプライン関数/ Bスプライン。

・1次元の基底関数に基づく非線形回帰一例

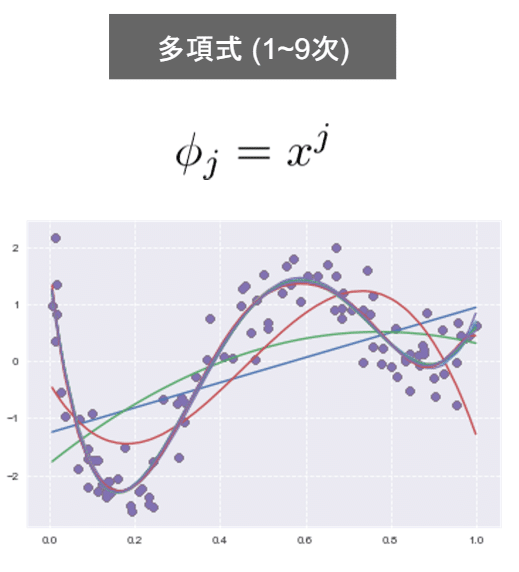
・2次元の基底関数に基づく非線形回帰一例

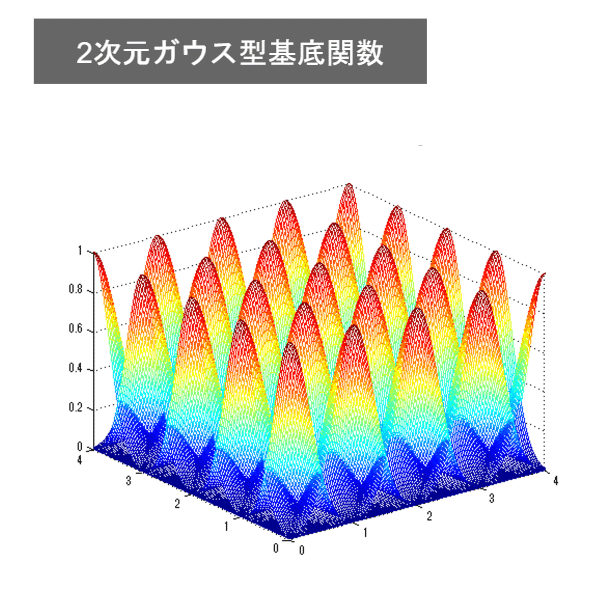
・未学習(underfitting)と過学習(overfitting)

未学習対策：表現力の高いモデルを利用する

過学習対策：1) 学習データの数を増やす。2) 不要な基底関数(変数)を削除して表現力を抑止。3) 正則化法を利用して表現力を抑止

・正則化法(罰則化法)：L2ノルムを利用▶Ridge推定量、L1ノルムを利用▶Lasso推定量

●未学習しているか過学習しているか：1)訓練誤差もテスト誤差もどちらも小さい▶汎化している可能性、2)訓練誤差は小さいがテスト誤差が大きい▶過学習、3)訓練誤差もテスト誤差もどちらも小さくならない▶未学習

python実装：

from sklearn.kernel_ridge import KernelRidge
import numpy as np

x = np.arange(20).reshape(-1,1)
y = np.asarray([20055.80,20032.35,20081.63,19994.06,19929.09,20080.98,20195.48,20098.38,20099.81,20118.86,19999.91,20020.86,20144.59,20099.75,19975.67,19955.20,20050.16,20079.64,19959.84,19925.18]).reshape(-1,1)

clf = KernelRidge(alpha=0.001, kernel='rbf')
clf.fit(x, y)

import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.plot(x, clf.predict(x))

考察：

・非線形回帰モデルは実質上多次元方程式のフィッティング問題に相当する

・非線形回帰モデルは多層ニューラルネットワークに相当する

・非線形回帰におけるパラメータの最適化は最小自乗法のほか、最尤推定やニュートン法なども使われている。

・非線形回帰のパラメータ最適化に関しては遺伝的アルゴリズムもよく使われる。