線形代数：固有値分解、特異値分解、疑似逆行列

線形代数は深層学習における計算の基本となっている。また、確率・統計にも深い関わりがある。

といってもライブラリなどで機械学習を現場で使っている人にはそれほど必要ではないかもしれない。

この記事では固有値分解と特異値分解を取り上げる。両方ともデータの特徴を抽出するのに役立つ。

特異値分解の知識があると疑似逆行列も理解できる。ただし、行列の積や行列式などは前提知識として必要になる。

また、全て実数値のみ（複素数なし）を扱う。

ノルム

ノルムとは長さや距離の概念を一般化したもの。ベクトル$${\vec{x}}$$に対して、いくつかのノルムが定義される。

$$
\vec{x} =
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{bmatrix}
$$

ちなみに、スペースを省くために横ベクトルを転置した形式で表記することもよくあります。

$$
\vec{x} = (x_1, x_2, \dots, x_n)^T
$$

L1ノルム

L1ノルムは、各要素の絶対値の総和。

$$
\|\vec{x}\|_1 = \sum\limits_{i=1}^{n}|x_i|
$$

L2ノルム

L2ノルムは、各要素の２乗の総和。

$$
\|\vec{x}\|_2 = \sum\limits_{i=1}^{n} x_i^2
$$

内積でも表現できる。

$$
\|\vec{x}\|_2 = \vec{x} \cdot \vec{x}
$$

L∞ノルム

L∞ノルムは、各要素の絶対値の最大値。

$$
\|\vec{x}\|_\infty = \max\limits_{i} |x_i|
$$

ノルム

単に「ノルム」と言う場合はL2ノルムの平方根。

$$
\|\vec{x}\| = \sqrt{\vec{x} \cdot \vec{x}}
$$

ベクトルの距離

ノルムに関連して2つのベクトル間の距離も一般化され種類がある。

固有値分解や特異値分解にはあまり関係がないがノルムを説明したのでここに記す。

ベクトル$${\vec{x} = (x_1, x_2, \dots, x_n)^\top}$$と$${\vec{y} = (y_1, y_2, \dots, y_n)^\top}$$に対して以下の距離が定義される。

マンハッタン距離

ニューヨークのマンハッタン街の道に沿って測ったかのような距離。日本人には碁盤の目に沿って測ったような距離といった方が分かりやすいかも。平安京とか。

$$
d(\vec{x}, \vec{y}) = \sum\limits_{i=1}^n |x_i – y_i|
$$

ユークリッド距離

これはいわゆる通常の距離。

$$
d(\vec{x}, \vec{y}) = \sqrt{\sum\limits_{i=1}^n (x_i – y_i)^2}
$$

ミンコフスキー距離

これは、マンハッタン距離やユークリッド距離を一般化したもの。

$$
d(\vec{x}, \vec{y}) = \left( \sum\limits_{i=1}^n |x_i – y_i|^p \right)^{\frac{1}{p}}
$$

$${p}$$は整数で、$${p=1}$$ならば、マンハッタン距離、$${p=2}$$ならば、ユークリッド距離ど同等。

マハラノビス距離

$${\vec{x}}$$と$${\vec{y}}$$が同じ確率分布に従うと仮定した場合における2つのベクトルの類似度の指標。

$$
D(\vec{x}, \vec{y} = \sqrt{ (\vec{x} – \vec{y})^\top \Sigma^{-1} (\vec{x} – \vec{y}) }
$$

行列の種類

いろいろあってややこしいのでまとめる。固有値分解や特異値分解を理解するのに必要な知識。

以下は全て正方行列の仲間。

正方行列

縦横が同じ数ある行列。n×n行列とかm×m行列と表現する。

これに対し、一般の行列はn×m行列あるいはm×n行列。

例：3×3行列

$$
A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}
$$

正則行列

逆行列$${A^{−1}}$$が存在する行列$${A}$$を正則行列と呼ぶ。

逆行列が存在するので正方行列でもある。

$$
AA^{-1} = A^{-1}A = I
$$

Aの行列式が0ではない：det(A)≠0。

直行行列

転置行列$${A^T}$$が逆行列になっている行列$${A}$$を直行行列と呼ぶ。

逆行列が存在するので正則行列でもある。よって正方行列でもある。

$$
A^T = A^{-1}
$$

対称行列

転置行列$${A^T}$$が元の行列と同じになる行列$${A}$$を対称行列と呼ぶ。

もちろん正方行列でもある。

$$
A^T = A
$$

代表的なものに共分散行列がある。

対角行列

対角の要素以外は全て０になっている行列Aを対角行列と呼ぶ。

転置したも同じなので対称行列でもある。よって正方行列でもある。

例：3×3の対角行列

$$
A = \begin{bmatrix} 9 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 3 \end{bmatrix}
$$

固有値分解などで登場する。計算が楽になる行列。

固有値、固有ベクトル

固有値（Eigenvalue）、固有ベクトル（Eigenvector）は以下に定義される。

正方行列Aとベクトルxが次の関係を持つとき、

$$
A\vec{x} = \lambda \vec{x}
$$

$${\lambda}$$はスカラーで固有値、ベクトル$${\vec{x}}$$を固有値$${\lambda}$$に属する固有ベクトルと呼ぶ。

正方行列$${A}$$と固有ベクトル$${\vec{x}}$$との積は元のベクトル$${\vec{x}}$$のスカラー倍になり方向は変わらない。

通常、固有ベクトルはノルム $${\|\vec{x}\|}$$ が１になるように定める。さもないと、拡大縮小することで無限に固有ベクトルを作れてしまうから。

しかし、ノルムが１でなくとも固有ベクトルとしての性質には変わらない。

具体例

固有値を求めるには上式を変形した次の関係を利用する。

$$
(A – \lambda I) \vec{x} = \vec{0}
$$

仮に、$${A \, – \, \lambda I}$$の逆行列が存在すると、$${\vec{x}}$$がゼロ・ベクトルになってしまう。

つまり、$${\vec{x}}$$がゼロ・ベクトルでないならば、$${A \, – \, \lambda I}$$には逆行列が存在しては困る。

よって $${A \, – \, \lambda I}$$ の行列式が0になる必要がある。さもないと固有値も固有ベクトルも存在しない。

$$
\det(A \, – \, \lambda I) = 0
$$

例えば、

$$
A = \begin{bmatrix} 4 & 1 \\ 3 & 2 \end{bmatrix}
$$

$${\det(A \, – \, \lambda I) = 0}$$ として、

$$
\begin{align*}
\det(A – \lambda I) &= \begin{vmatrix} 4 – \lambda & 1 \\
3 & 2 – \lambda \end{vmatrix} \\
&= (4-\lambda)(2-\lambda)-3 \\
&= 0
\end{align*}
$$

上式を解くと、

$$
\therefore \lambda = 1, 5
$$

次に、固有ベクトルを

$$
\vec{x} = \begin{bmatrix} x_1 \\
x_2
\end{bmatrix}
$$

とすると、$${A\vec{x} \, – \, \lambda \vec{x} = 0}$$ より、$${\lambda = 1}$$に属する固有ベクトルは、

$$
\begin{bmatrix}
4-1 & 1 \\
3 & 2-1
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} =
\begin{bmatrix}0 \\
0
\end{bmatrix} \\
\ \\
\therefore 3x_1 + x_2 = 0
$$

上記の条件を満たす $${x_1, x_2}$$ は、

$$
\begin{align*}
x_1 &= -\frac{1}{3}t \\
x_2 &= t
\end{align*}
$$

となる。tは任意の実数。

ノルムが１になるように $${x_1^2 + x_2^2 = 1}$$ を満たすように調節する。

$$
\vec{x} =
\begin{bmatrix}
-\frac{1}{\sqrt{10}} \\\\
\frac{3}{\sqrt{10}}
\end{bmatrix}
$$

となる。もちろん、負号を入れ替えた$${(\frac{1}{\sqrt{10}}, -\frac{3}{\sqrt{10}})^T}$$でも良い。

ベクトルの向きが逆になるだけなので、どちらかを選ぶ。

同様に、固有値$${\lambda=5}$$に対して、

$$
\vec{x} = \begin{bmatrix}
\frac{1}{\sqrt{2}} \\\\
\frac{1}{\sqrt{2}}
\end{bmatrix}
$$

もちろん、負号を入れ替えても良い。

行列式と固有値：
行列式の知識を使って固有値を求めたが、実は行列式は固有値を全て掛け合わせたものに等しい。

また、行列Aの行列式det(A)の絶対値は、行列Aによる乗算が空間をどのくらい拡大（あるいは圧縮）するかを示している。

$${(A – \lambda I)\vec{x} = \vec{0}}$$で$${\det(A – \lambda I)=0}$$となるのは行列$${(A – \lambda I)}$$による乗算が空間を原点に圧縮しているとも見れる。ちょっとしたブラックホールみたいでもある。

Numpy

上述の例では２x２の行列だったが３x３やそれ以上の場合も同じアプローチで計算できる。

ただし、行列式の計算が面倒臭いので、プログラムを使えば良い。

import numpy as np


A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]]) 

print('A=')
print(A) 
print()

values, vectors = np.linalg.eig(A) 

print('固有値')
print(values) 
print()

print('固有ベクトル')
print(vectors)

A=
[[1 2 3]
 [4 5 6]
 [7 8 9]]

固有値
[ 1.61168440e+01 -1.11684397e+00 -1.30367773e-15]

固有ベクトル
[[-0.23197069 -0.78583024  0.40824829]
 [-0.52532209 -0.08675134 -0.81649658]
 [-0.8186735   0.61232756  0.40824829]]

第一列の固有ベクトルを使ってみる。

λ = values[0]
x = vectors[:, 0]

print('λ * x')
print(λ * x)

print('A @ x')
print(A @ x)

λ * x
[ -3.73863537  -8.46653421 -13.19443305]
A @ x
[ -3.73863537  -8.46653421 -13.19443305]

ちゃんと固有値と固有ベクトルになっています。ただし、結果が行ベクトルになっています。

列ベクトルの形を崩したくなければ、固有ベクトルxxの取り出し方を以下のようにします。

λ = values[0]
x = vectors[:, 0:1]

print('λ * x')
print(λ * x)

print('A @ x')
print(A @ x)

λ * x
[[ -3.73863537]
 [ -8.46653421]
 [-13.19443305]]
A @ x
[[ -3.73863537]
 [ -8.46653421]
 [-13.19443305]]

ちなみに、Jupyter notebookのセルで \lambda と打ってTabキーを押すとギリシャ文字の λ に変換されます。

対称行列

対称行列の固有ベクトルは直行する。

固有値 $${\lambda_1, \lambda_2\ (\lambda_1 \ne \lambda_2)}$$ に対する固有ベクトルを $${\vec{x}_1, \vec{x}_2}$$ とし、内積 $${\vec{x}_1 \cdot \vec{x}_2}$$ に $${\lambda_1}$$ をかけると、

$$
\begin{align*}
\lambda_1 \vec{x}_1 \cdot \vec{x}_2 &= (\lambda_1 \vec{x}_1)^\top \vec{x}_2 \quad \text{内積を行ベクトルと列ベクトルの積に} \\
&= (A \vec{x}_1)^\top \vec{x}_2 \\
&= \vec{x}_1^\top A^\top \vec{x}_2 \\
&= \vec{x}_1^\top A \vec{x}_2 \ \qquad \text{対称行列は転置しても同じ} \\
&= \vec{x}_1^\top \lambda_2 \vec{x}_2 \\
&= \lambda_2 \vec{x}_1^\top \vec{x}_2 \\
&= \lambda_2 \vec{x}_1 \cdot \vec{x}_2 \ \,\quad \text{内積に戻す}
\end{align*}
$$

これは、

$$
\lambda_1 \vec{x}_1 \cdot \vec{x}_2 = \lambda_2 \vec{x}_1 \cdot \vec{x}_2
$$

を意味するが、$${\lambda_1 \ne \lambda_2}$$ なので、

$$
\vec{x}_1 \cdot \vec{x}_2 = 0
$$

でなければならない。よって対称行列における異なる固有ベクトルは直行する。

以上の知識があれば固有値分解が理解できる。

固有値分解

固有値分解（Eigendecomposition）は以下に定義される。

固有値と固有ベクトルを使うと正方行列Aは次のように固有値分解できる。

$$
A = Q \Lambda Q^{-1}
$$

Qは固有ベクトルを要素として持つ行列。列ベクトル $${x_i\ (i=1 \sim n)}$$ が固有ベクトル。

$$
Q = \left[ \vec{x}_1 \quad \vec{x}_2 \quad \dots \quad \vec{x}_n \right]
$$

$${\Lambda}$$はギリシャ文字のラムダの大文字で、ここでは固有値を対角要素としてもつ対角行列を表す。

$$
\Lambda =
\begin{bmatrix}
\lambda_1 & 0 & \dots & 0 \\
0 & \lambda_2 & \dots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \dots & \lambda_n
\end{bmatrix}
$$

Qの対角にある固有値は大きい値から小さい値へと順番に並べる。つまり、

$$
\lambda_1 > \lambda_2 > \dots > \lambda_n
$$

利点

分解することで行列（データ）の特徴が見える。

小さい（ほとんどゼロの）固有値を無視することで次元削減ができる。

また、$${A^n}$$の計算が楽になる。

$$
\begin{align*}
A^n &= (Q\Lambda Q^{-1})^n \\
&= (Q\Lambda Q^{-1}) (Q\Lambda Q^{-1}) \dots (Q\Lambda Q^{-1}) \\
&= Q\Lambda (Q^{-1} Q) \Lambda (Q^{-1} Q) \Lambda \dots \Lambda (Q^{-1} Q) \Lambda Q^{-1}) \\
&= Q \Lambda^n Q^{-1}
\end{align*}
$$

対角行列$${\Lambda}$$のn乗は対角要素をn乗するだけ。

証明

固有値分解が可能なことを証明するには式を変形して、

$$
\begin{align*}
A &= Q\Lambda Q^{-1} \\
AQ &= Q\Lambda
\end{align*}
$$

が示せればいい。よって、

$$
\begin{align*} AQ & = A \left[\vec{x}_1 \ \vec{x}_2 \ … \ \vec{x}_n\right]\\
&= \left[A \vec{x}_1\ A \vec{x}_2\ …\ A \vec{x}_n\right] \\
&= \left[\lambda_1 \vec{x}_1\ \lambda_2 \vec{x}_2\ …\ \lambda_n \vec{x}_n\right] \\
&= \left[\vec{x}_1 \ \vec{x}_2 \ … \ \vec{x}_n\right]
\begin{bmatrix}
\lambda_1 & 0 & \dots & 0 \\
0 & \lambda_2 & \dots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \dots & \lambda_n
\end{bmatrix} \\
&= Q \Lambda
\end{align*}
$$

上記の計算では、列ベクトル $${x_i\ (i=1 \sim n)}$$ が固有ベクトルであることを利用している。

Numpy

import numpy as np


A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]]) 

print('A=')
print(A) 
print()

# 固有値と固有ベクトル
values, vectors = np.linalg.eig(A) 

Λ = np.diag(values)
Q = vectors

QΛQinv = Q @ Λ @ np.linalg.inv(Q)

print('QΛQinv=')
print(QΛQinv)

A=
[[1 2 3]
 [4 5 6]
 [7 8 9]]

QΛQinv=
[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]

$${Q\Lambda Q^{-1}}$$の値が浮動小数点になっていることを除けばAの値と合致します。

もし、気になるのであればAを定義するときにデータ型を指定すれば良い。

A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]], dtype=np.float64) 

print('A=')
print(A)

A=
[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]

直行行列

前述したように、Aが対称行列だと、異なる固有値は直行する。さらに、固有ベクトルのノルムを1にしておくと、固有値ベクトルを集めた行列Qは直行行列になる。

Qが直行行列だと、$${QQ^\top=I}$$なので$${Q^\top=Q^{-1}}$$となり、

$$
A = Q\Lambda Q^T
$$

の関係が成り立つ。固有値分解と言うとこれを指すことが多い。

対称行列を使ってNumpyで実際にやってみます。

import numpy as np


# 対称行列
A = np.array([
    [1, 2, 3],
    [2, 5, 6],
    [3, 6, 9]], dtype=np.float64) 

print('A=')
print(A) 
print()

# 固有値と固有ベクトル
values, vectors = np.linalg.eig(A) 

Λ = np.diag(values)
Q = vectors

QΛQT = Q @ Λ @ Q.T

print('QΛQT=')
print(QΛQT)

A=
[[1. 2. 3.]
 [2. 5. 6.]
 [3. 6. 9.]]

QΛQT=
[[1. 2. 3.]
 [2. 5. 6.]
 [3. 6. 9.]]

理論通りに結果が出ると楽しい。

ちなみに、Qが直行行列であることを確かめてみます。

QQT = Q @ Q.T

print('QQT=')
print(QQT)

QQT=
[[ 1.00000000e+00  5.55111512e-17 -1.80411242e-16]
 [ 5.55111512e-17  1.00000000e+00  0.00000000e+00]
 [-1.80411242e-16  0.00000000e+00  1.00000000e+00]]

対角は１でそれ以外は０のはずですが、非常に小さい０でない値が入っている。

これはコンピュータによる数値計算の精度に限界があるため。

なので実際にプログラムを組むときはある程度小さい値はゼロと見なすなど必要に応じて判断する必要がある。

逆に、小さすぎる値は０になってしまうこともある。

固有値分解は正方行列（特に対称行列）を分解するのに有効だが、世の中には正方でないデータが多い。

よって次の特異値分解が役に立つ。ただし、特異値分解を理解するには固有値分解の知識が必要となる。

特異値分解

特異値分解（Singular Value Decomposition）は略してSVDと呼ばれる。

全ての行列にSVDは存在する。よって固有値分解より条件がゆるく使い勝手が良い。

分解される行列は正方行列でなくともOK。

行列Aをm×n行列とすると、

$$
A = U \Sigma V^\top
$$

に分解することができる。

Uはm×mの直行行列、Σはm×n対角行列、$${V^T}$$はn×nの直行行列Vの転置行列。

Σの構造は以下のようになる。左上に特異値を対角要素に持った対角行列をもち、それ以外は全て０。

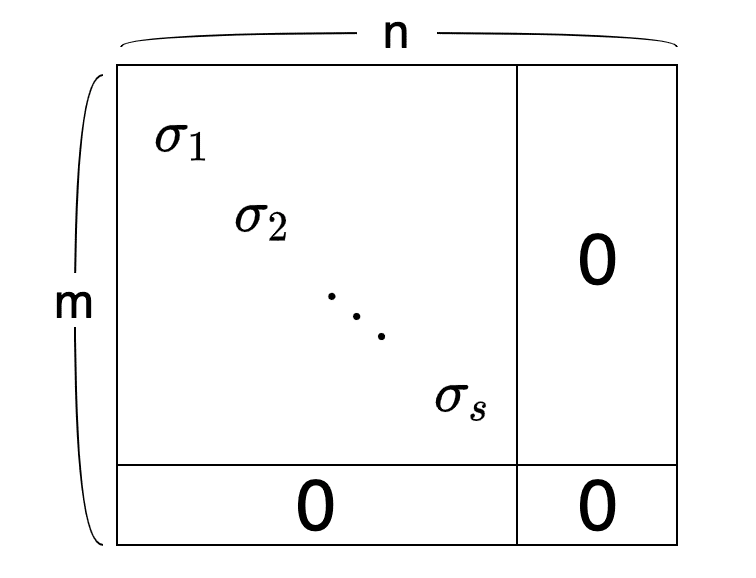
この$${\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_s \ge 0}$$を特異値と呼ぶ。この特異値の数は行列Aのランクに一致する。

ランクは行列内にある独立な列ベクトルの数。独立とはある列ベクトルを他の列ベクトルの組み合わせで表現できないこと。

計算

基本的な考え方は、Aが正方行列ではないので$${AA^T}$$あるいは$${A^TA}$$で正方行列を作り、固有値問題にする。

その際に計算が楽になる方を選ぶ。

まず、$${AA^T}$$を計算すると、

$$
\begin{align*}
\\
AA^\top &= U \Sigma V^\top (U \Sigma V^\top)^\top \\
&= U \Sigma V^\top V \Sigma^\top U^\top \\
&= U \Sigma \Sigma^\top U^\top \\
&= U {\Sigma_m}^2 U^\top
\end{align*}
$$

となる。Vが直行行列なので$${V^TV=I}$$になることを利用した。

また、$${\sum_m^2 = \sum\sum^T}$$としている。$${\sum_m^2}$$はm×mの対角行列。

$${AA^T}$$に右から$${U}$$を掛ければ、

$$
\begin{align*}
\\
AA^\top U &= U \Sigma_m^2 \, U^\top U \\
&= U \Sigma_m^2
\end{align*}
$$

となる。ここでは、Uが直行行列であることを利用した。

よって、$${\sum_m^2}$$の対角が$${AA^T}$$の固有値$${\sigma_i^2}$$で、Uの列ベクトルが固有ベクトル。

つまり、$${AA^T}$$の固有値と固有ベクトルを解けば、Uと$${\sigma_i}$$がわかる。

同様に、$${A^TA}$$を計算すると、

$$
\begin{align*}
\\
A^\top A &= (U \Sigma V^\top)^\top U \Sigma V^\top \\
&= V \Sigma^\top U^\top U \Sigma V^\top \\
&= V \Sigma^\top \Sigma V^\top \\
&= V {\Sigma_n}^2 V^\top
\end{align*}
$$

となる。Uが直行行列なので$${U^TU=I}$$になることを利用した。

また、$${\sum_n^2 = \sum^T \sum}$$としている。$${\sum_n^2}$$はn×nの対角行列。

$${A^TA}$$に右からVを掛ければ、

$$
\begin{align*}
\\
A^\top A V &= V \Sigma_n^2 V^\top V \\
&= V \Sigma_n^2
\end{align*}
$$

となる。ここでは、Vが直行行列であるとこを利用した。

よって、$${\sum_n^2}$$の対角が$${A^TA}$$の固有値$${\sigma_i^2}$$で、Vの列ベクトルが固有ベクトル。

つまり、$${A^TA}$$の固有値と固有ベクトルを解けば、Vと$${\sigma_i}$$がわかる。

以上で、$${U, \Sigma, V}$$が求まるので、m×n行列Aを$${U\Sigma V^T}$$に分解することができる。

実際には$${AA^T}$$か$${A^TA}$$のどちらか小さい方を使って固有値問題を解く。

その固有値を使ってUとVの固有ベクトルを計算すれば良い。

具体例

画像データ一枚につき10,000の画素データがある。

これを列ベクトルとして、100枚分の画像を 10,000 × 100 の行列Aに入れる。

この場合、$${AA^T}$$は 10,000 × 10,000 だが、$${A^TA}$$Aは100×100なのでより小さい。

よって$${A^TA}$$で固有値問題を解き、UとVの固有ベクトルを計算する。

このようにしてデータから主成分を取り出すことができる。

注意点

自分で計算する際に注意する点がある。

まず、特異値は$${AA^T}$$か$${A^TA}$$で求めた固有値の平方根であること。

その際に、特異値分解の定義に従って正の平方根を使う。

また、直行行列UとVの列ベクトルは正方行列$${AA^T}$$と$${A^TA}$$の固有ベクトルである。

直行行列UとVの列ベクトルはAの固有ベクトルではない。

最後に、特有値分解$${A=U \Sigma V^T}$$では$${V}$$は$${V^T}$$として使われることを忘れないように。

Numpy

NumpyでSVDをやってみる。

import numpy as np


A = np.array([
    [1, 2],
    [3, 4],
    [5, 6]], dtype=np.float64) 

print('A=')
print(A) 
print()

U, S, VT = np.linalg.svd(A) 

print('U=')
print(U) 
print()

print('S=')
print(S)
print()

print('VT')
print(VT)
print()

A=
[[1. 2.]
 [3. 4.]
 [5. 6.]]

U=
[[-0.2298477   0.88346102  0.40824829]
 [-0.52474482  0.24078249 -0.81649658]
 [-0.81964194 -0.40189603  0.40824829]]

S=
[9.52551809 0.51430058]

VT
[[-0.61962948 -0.78489445]
 [-0.78489445  0.61962948]]

Numpyは直接$${V^T}$$を返してくる。また、固有値はベクトル形式。

必要ならば、固有値ベクトルSを特異値分解における$${\Sigma}$$の形式にする。

Σ = np.zeros_like(A, dtype=np.float64)
Σ[:2] = np.diag(S)

print('Σ=')
print(Σ)
print()

Σ=
[[9.52551809 0.        ]
 [0.         0.51430058]
 [0.         0.        ]]

これを使って$${A=U \Sigma V^T}$$を確認する。

UΣVT=
[[1. 2.]
 [3. 4.]
 [5. 6.]]

行列Aの値が復元されている。

疑似逆行列

正方行列でも逆行列が存在するとは限らないが、正方行列でないと逆行列は存在しない。

疑似逆行列を使うと正方行列でなくとも疑似的な逆行列が使える。

例えば、m×nの行列Aがあるとする。

$$
A\vec{x} = \vec{y}
$$

疑似逆行列$${A^+}$$を使えば、

$$
\vec{x} = A^+ \vec{y}
$$

と変換することができる。

疑似逆行列$${A^+}$$は、

$$
A^+ = V D^+ U^T
$$

と定義される。VとUは特異点分解$${A=U\Sigma V^T}$$から来ている。

$${D^+}$$は$${\Sigma}$$を転置して対角成分を全て逆数にしたもの。

m×nの行列$${\Sigma}$$が以下のように定義されていると、

$$
\Sigma = \begin{bmatrix}
\sigma_1 & & & & & & \\
& \sigma_2 & & & & & \\
& & \ddots & & & & \\
& & & \sigma_s & & & \\
& & & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 0
\end{bmatrix}
$$

n×mの行列$${D^+}$$は次のように定義される。

$$
D^+ = \begin{bmatrix}
\frac{1}{\sigma_1} & & & & & & \\
& \frac{1}{\sigma_2} & & & & & \\
& & \ddots & & & & \\
& & & \frac{1}{\sigma_s} & & & \\
& & & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 0
\end{bmatrix}
$$

ここで$${D^+\Sigma = I}$$であることに注目すると、

$$
\begin{align*}
A^+ A &= (V D^+ U^\top)(U \Sigma V^\top) \\
&= V D^+ \Sigma V^\top \\
& = V V^\top \\ & = I
\end{align*}
$$

となる。また、特異値分解の定義から、UとVは直行行列なので、$${U^TU=I}$$と$${VV^T=I}$$となることを利用した。

まとめると、

$$
\begin{align*}
A \vec{x} &= \vec{y} \\
A^+A \vec{x} &= A^+ \vec{y} \\
\vec{x} &= A^+ \vec{y} \\
\vec{x} &= V D^+ U \vec{x}
\end{align*}
$$

つまり、Aの特異値分解をすれば、Aの疑似逆行列として$${A^+}$$を計算できる。

注意としては、Aがm×n行列ならば$${A^+}$$はn×m行列になること。

Numpy

Numpyで試してみる。

import numpy as np


A = np.array([
    [1, 2],
    [3, 4],
    [5, 6]], dtype=np.float64) 

AP = np.linalg.pinv(A)

print('AP @ A')
print(AP @ A)

AP @ A
[[ 1.0000000000000004e+00  0.0000000000000000e+00]
 [-4.4408920985006262e-16  9.9999999999999956e-01]]

対角がほぼ１で、それ以外はほぼ０なので$${A^+A = I}$$が成り立っているのがわかる。