ARC107を解いたまとめ
ARC107を解いたので解法をまとめておきます.B問題まで解けました.
A問題
問題はこちら
今回の問題は,3つの変数に対してそれぞれ与えられた値までの掛け算をした時の和を求め,該当数値で割ったあまりを出力する,という問題です.
例えばA=1,B=2,C=3とすると
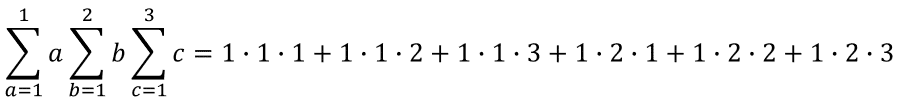
このように表されます.
これは素直に実装すると三重for文で解決することができます.ざっと書くと
long long sum = 0;
for (int a = 1; a <= A; a++) {
for (int b = 1; b <= B; b++) {
for (int c = 1; c <= C; c++) {
sum += a * b * c;
}
}
}こうなります.
ただ,これの計算量はO(n^3)なので,とても遅いことが分かると思います.当然このまま出すとTLEとなってしまいます.そのため,工夫が必要です.
まず与えられた式を見てみます.すると,掛け算の和ですから,共通因数を括りだすという手法が使えそうです.先ほどの例で括りだしてみると

という式を得ることができます.これを使うとfor文が1つ減らすことができます.
また,1~Nまでの自然数の和は

で表されるため,予めaの総和を求めておけばかなり計算量が減らすことができます.
ここで,自然数の和が上記の式になることを改めて証明してみましょう.数学は何事も証明して理解を深めていく学問だと高校の数学の先生に教わったので,照明が多くなりますが,ご了承ください.
まず,自然数の和を2つ用意します.ただし,片方は逆順に並べています.

この2つを足し算すると,このようになります.

足し算結果の右辺は(n+1)がn個ありますから,次の式のようにまとめることができます.

あとは両辺2で割れば,証明したいシグマの結果を得ることができます.

では本題に戻ります.aと同様にbやcも和を予め求めておくようにすれば,この計算自体はO(1)で解くことができます.
つまり,問題の式を変形すると
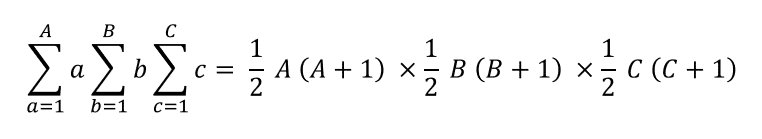
となります.あとはこの結果を998244353で割れば,ACすることができます.
B問題
問題はこちら
1≦ a, b, c, d ≦Nであって,a + b - c - d = Kとなる(a,b,c,d)の組み合わせの総数を求めよ,という問題.これはA問題と同様に単純に実装すると四重for文,つまりO(n^4)となってしまうことから,何かしら工夫が必要だということが分かります.
まずは与えられた式を変形してみます.(a + b - c - d)がKと等しい組み合わせを見つければよい,すなわち
(a + b) - (c + d) がKと等しい組み合わせを見つければよい
と言い換えることができます.ということは,aとbの和とcとdの和の差がKと等しくなれば良いということですね.
aとbの和をSab,cとdの和をScdとすると
![]()
この式を満たせばよさそうです.さらに,

と式変形すればSabのみを調べればよいので,for文は1つで済むことが分かります.実際にコードで書くと
for (int Sab = 0; Sab < xx; Sab++) {
int Scd = Sab - k;
...
}とすれば良さそうです.残る問題は
・Sabをどこまで調べるか.
・Sabの組み合わせは何通りか.
・合計いくつになるか.
の3つだと思います.
まず1つ目,Sabをどこまで調べるか,ですが,Sabはaとbの組み合わせの総数ですから,2nまで調べればすべてが網羅できると思います.(もっと少なくてもいいのかもしれませんが,今回は2nでできました.)
では肝心の2つ目,Sabの組み合わせについて考えていきます.
例えばSabが5の時,考えられる組み合わせは,
(a, b) = (1, 4), (2, 3), (3, 2), (4, 1)の計4通りとなります.
ほかにも,Sabが10の時,考えられる組み合わせは,
(a, b) = (1, 9), (2, 8), (3, 7), (4, 6), (5, 5), (6, 4), (7, 3), (8, 2), (9, 1)の計9通りとなります.
つまり,Sabがpとなるとき,考えられる組み合わせは,(p-1)通りとなります.これでこの問題は解決できそうです.
ただし,これはNがpより大きい場合に限ります.なぜならば,N=7のとき,Sabが10となる組み合わせを考えると,
(a, b) = (3, 7), (4, 6), (5, 5), (6, 4), (7, 3)の計5通りとなるからです.a,b,c,dそれぞれNを超えてはいけませんから,このように組み合わせの数が変わってきます.
この場合の組み合わせの数を数える方針として,(全体)-(不要なもの)として計算します.全体はp-1通りなので,不要なものの個数を考えます.
このa,bの組み合わせの性質から,(p-1, 1) ~ (N + 1, p - (N + 1))が不要なものの個数(の半分)ということになります.この個数は(p - 1 - N)個であり,これがもう1セットあるので全体として 2 * (p - 1 - N)個が不要,ということになります.
よって,(p - 1) - 2 * (p - 1 - N) = 2 * N + 1 - p個の組み合わせ,ということになります.
3つ目はSabとScdの組み合わせの総数が求める組み合わせの総数ということになります.Sabの組み合わせとScdの組み合わせは,a,b,c,dに大小関係はないため,SabとScdの組み合わせの総数を掛け算すれば良いことが分かります.
以上の考察からコードにまとめると,次のようになります.
long long ans = 0; // 答えを格納する変数
for (long long Sab = 2; Sab <= 2 * n; Sab++) { // 最小値が1なので1+1=2から始めても問題はない
long long Scd = Sab - k;
if (Scd > 2 * n || Scd < 2) continue; // kを引くので,2より小さいor2nより大きくなる可能性がある
long long left = (Sab > n) ? (2 * n - Sab + 1) : (Sab - 1);
long long right = (Scd > n) ? (2 * n - Scd + 1) : (Scd - 1);
ans += left * right;
}こうすればO(n)で解くことができました.
感想
初めてARCを開催中に解いてみましたが,B問題が限界でした…
ARCでもC問題・D問題も解いて戦っていけるようにより多くの問題を解いて成長していきたいです.
この記事が気に入ったらサポートをしてみませんか?
