熱力学の偏微分は「変」な微分

　「偏微分」という用語も、なかなか難解な用語ですね。

　偏微分自体は簡単です。例えば関数 f として、

f(u,v,w,x,y,z) = ux^2 + vy + (w^3)z^4

なんていう「多変数関数」を適当に考えた場合、これを

「x について偏微分しなさい」

と言われたら、

x 以外の変数は全て定数

とみなして、

∂f/∂x = 2ux

ってすればいいんです。

これは、いくつか変数がある中で、

x だけを変化させたときに、f がどう変化するかを調べる

という操作になるのですが、これが果たして文字通り

「偏り」を調べた

ことになるのでしょうか。

　偏微分の反対は、「全微分」という事になります。（全微分については以下の記事の最後を参照して下さい。）

　これからすると、

x 方向に「偏っている」事を調べるには、むしろ全微分が必要

なのではないでしょうか。どの方向に偏っているかなどは、これで調べた結果わかるものです。

さらに言えば、　

「偏」と「全」

は日本語としても対応していません。実際に英語で「偏微分」は、

Partial differentiation（「部分微分」）

なのです。何故そう訳さなかったのでしょうか。ぶんぶん五月蠅いから嫌だったのでしょうか。蠅だけに。

　はい、「五月蠅い」というのを書くための前振りでした～（長いよ）。

●熱容量とは

　前回は、「閉じた系」、「断熱系」、そして「孤立系」におけるエネルギ保存則の式を導きました。

　もう一度書くと、「内部エネルギ"U"」という量を導入して、

dU = TdS - PdV --- ( 1 )

でした。この式の着目すべき点は、

温度"T"が一定の範囲でやり取りした微小な熱"TdS"

と、

圧力"P"が一定の範囲でやり取りした微小な仕事"PdV"

を考えているという事です。

　ここでまた新たに、「熱容量」という概念を導入します。熱容量とは熱のキャパシティなわけです（ルー語または長嶋方式、どちらにしろ古い）。

　「容量」とは入れ物の大きさの事ですから、

「熱がどれだけ入るか」

というのを表す値です。

　ところで、皆さんはスーパーなどで、

「詰め放題」

ってやったことありますか？決められた大きさの袋の中に、商品を詰められるだけ詰めて、いくら詰めても１袋いくらっていうあれです。

　そこで、沢山袋に詰めるときはどうするでしょうか。押しつぶしても問題ない商品であれば、袋が破けない程度に強く押し込みますよね。

　さて、熱量

δQ = TdS

に関して、強さを示す「示強変数」は何だったでしょうか？

　そう、温度です。つまり、

熱を沢山入れるには、温度を上げればいい

のです。そして、

「一定の熱与えた時どれだけ温度が上がるか」

または、

「一定の温度上昇でどれだけの入熱になるか」

を表わす指標が、この「熱容量」になります。

　式としては、

"⊿Q"の熱を与えた時、温度が"⊿T"上がったとすると、"C"を熱容量として、

⊿Q = C⊿T

という式が成り立ちます。これには様々なアナロジーがありますが、「コンデンサ」や「ばね」のモデルが最も良いでしょう（下図）。

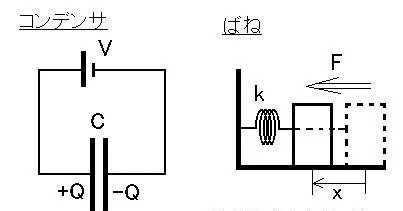
　「コンデンサ」の場合は、

電荷"Q"を与えた時、電極間の電圧が"V"となったとすると、"C"を静電容量として、

Q = CV

です。また、「ばね」の場合は、

変位"x"を与えた時、ばねの反発力がが"F"となったとすると、"k"をばね定数として、

x = F/k

です。ばねの場合、

ばね定数の逆数を「変位容量」と考える

ことができます。

　ただ気をつけるべき点は、この場合のアナロジーは「容量」の意味に限るものであって、各変数の性質は必ずしも対応していません。ちなみに、熱容量に関しては、物質の量に比例するので、「示量性」となります。

●過程によって変わる熱容量と偏微分

　ところで、何度も申し上げるように、「開いた系」で熱を与える過程は「等圧過程」であり、「熱膨張」という現象があります。「膨張」は

⊿V > 0

であって、それが起こったのが「真空中」、つまり

P = 0

でない限り、

系は外界に仕事"P⊿V”をする

事になります。つまり、熱膨張が起こる時は、エネルギ保存則により、

その仕事の分、系に与えられた熱が費やされている

はずです。

　本来「熱容量」は、

物質の種類とその量が決まれば決まってほしい値

であるので、これは少々厄介な問題です。そこで、以下のように考えます。

　閉じた系の（準静的な）状態変化として挙げた、

「定積過程」「定圧過程」「等温過程」「断熱過程」

のうち、

等温過程と断熱過程は、熱の出入りに対する温度変化が無い

ので、まずは定積過程について、熱容量を考えてみましょう。

　定積過程は文字通り

⊿V = 0

であり、膨張しないので、( 1 )式は

dU = TdS

と、入ってきた熱が全て内部エネルギーの増加になります。つまりここで、「定積熱容量"Cv"」というものが定義できて、

Cv = ⊿U/⊿T

とできるわけです。これは、

内部エネルギ"U"の温度"T"による変化

という事なので、微分を使って表現します。しかし、

Cv = dU/dT

と書くことはできません。何故なら、内部エネルギは、本来体積や圧力、エントロピーでも変わる可能性があるからです。

　つまり、内部エネルギを関数とみなすと、

U = U(V, P, S, T)

という「多変数関数」であり、「偏微分」の形で

Cv = (∂U/∂T) --- ( 2 )

と書きます。

　数学上はこの表記で問題無いのですが、熱力学上は、常にこの関係が成り立つわけではありません。あくまで、

「体積"V"一定」の変化でのみ、この式が成立する

ことになります。

　なので、( 2 )式は

Cv = (∂U/∂T)v

と、

一定にする状態量、この場合は体積"V"の添え字を偏微分の式に付して

表します。もう少し数学的に言うと、

U = U(V, T)

と、

"U"を、独立変数"V"と"T"の関数とみなした上で

（以下の補足参照）温度"T"で偏微分するということを表わしています。

　では、

定圧過程での熱容量

はどう書けるでしょうか。というのはまた次回にします。

■補足：熱力学における偏微分

　熱力学では、上のような「添え字付き」偏微分が分かっていないと、もうお手上げ状態になります。

　数学では例えば、

z = f (x, y)

の普通の偏微分も、添え字をつけると

(∂z/∂x)y, (∂z/∂y)x

と書けます。しかし数学の場合は、熱力学のように、

z = f (x, y) = g (u, v)

と、

変数によって異なる関数の形を取る

関数の定義は許されず、

z = f (x, y)

といったら

z = f (u, v)

でなければなりません。だから、「添え字」など付けなくても混乱する恐れが無いのです。

　しかし、熱力学では、

通る過程によって、状態量の取る変数が違う

ため、「関数の式」も違ってきます。そのため、

「どういう過程で考えているのか」、

つまり、

「どの変数の関数になっているか」

を明示する必要があり、添え字をつけるわけです。

　例えば、

( )v, ( )p, ( )s, ( )t

となっていればそれぞれ、

「定積過程」、「定圧過程」、「等エントロピー（可逆断熱）過程」、「等温過程」

を表していて、

それぞれの過程で成立する関数関係

を考えることになります。

　これが、純粋な「数学」と「物理数学」で大きく異なる点の一つとなっています。「物理数学」では、必ず変数が何らかの物理量を表していて、もともとの

「物理的な定義」

を現象から考えて、数式を立てる必要があるわけです。