生存時間曲線つづき

同じデータでマルコフ連鎖モンテカルロ法MCMCで
サンプリング数を増やしてベイス推定してみました。

model = "
 data {
 int<lower=1> N;
 int<lower=1> T;
 int<lower=1, upper=T> Time[N];
 int<lower=0, upper=1> Cens[N];
 }
 parameters {
 real<lower=0> sigma_log_hazard;
 vector<upper=0>[T] log_hazard;
 }
 transformed parameters {
 vector[T] log_S;
 vector[T] log_f;
 log_S[1] = log1m_exp(log_hazard[1]);
 log_f[1] = log_hazard[1];
 for (t in 2:T) {
 log_S[t] = log_S[t-1] + log1m_exp(log_hazard[t]);
 log_f[t] = log_S[t-1] + log_hazard[t];
 }
 }
 model {
 sigma_log_hazard ~ cauchy(0, 1);
 log_hazard ~ cauchy(0, 10);
 for (t in 2:T) {
 log_hazard[t] ~ normal(log_hazard[t-1], sigma_log_hazard);
 }
 for (n in 1:N) {
 if (Cens[n] == 1) {
 target += log_f[Time[n]];
 }
 else {
 target += log_S[Time[n]];
 }
 }
 }
 generated quantities {
 vector[T] hazard;
 vector[T] S;
 hazard = exp(log_hazard);
 S = exp(log_S);
 }
 "

モデルは以上のようになります。2段階差分です。

treat0とtreat1で層別化して計算して、それぞれのHazardを計算して
カプランマイヤー曲線を作成していきます。

treats=c("0","1")
result = lapply(seq_along(treats), function(i){
 tr = treat1[treat1$treat == treats[i],]
 data_stan = list(N=nrow(tr), T=max(tr$days), Time=tr$days, Cens=tr$response)
 stan_fit = stan(model_code = model, data=data_stan,
 chains=4, iter=4000, warmup=2000, thin=1, seed=3,
 control=list(adapt_delta=0.8, max_treedepth=10)
 )
stan_fit
 })

結果を取り出します。

my_extract = function(x,name){
 tb = summary(x, probs=c(0.025,0.975),pars=name)$summary
 df = data.frame(tb[,c("mean","2.5%","97.5%"), drop=F])
 colnames(df) = c("mean","lower","upper")
 df
 }

 df_S =lapply(result,function(x){
 df = my_extract(x,"S")
 df$time = 1:nrow(df)
 df
 })

 df_h =lapply(result,function(x){
 df = my_extract(x,"hazard")
 df$time = 1:nrow(df)
 df
 })

df_h
df_s mean lower upper time
hazard[1] 0.2096954 0.08387344 0.3903780 1
hazard[2] 0.1712744 0.04802357 0.3230828 2
hazard[3] 0.1963125 0.06834335 0.3630519 3
hazard[4] 0.2472448 0.09101379 0.5131296 4

[[2]]
mean lower upper time
hazard[1] 0.3977416 0.23382685 0.5844687 1
hazard[2] 0.2559223 0.07873641 0.4477860 2
hazard[3] 0.3500685 0.15705598 0.5648722 3
hazard[4] 0.5894864 0.28229141 0.8904038 4

df_S
[[1]]
mean lower upper time
S[1] 0.7903046 0.6096220 0.9161266 1
S[2] 0.6570841 0.4491418 0.8388618 2
S[3] 0.5312813 0.3129014 0.7445881 3
S[4] 0.4032806 0.1953451 0.6344232 4

[[2]]
mean lower upper time
S[1] 0.6022584 0.41553132 0.7661732 1
S[2] 0.4489916 0.27340555 0.6331652 2
S[3] 0.2941656 0.14536261 0.4755628 3
S[4] 0.1210898 0.02779909 0.2673877 4

kphaz = kphaz.fit(time=treat1$days, status=treat1$response, strata=treat1$treat)
df_kphaz = lapply(1:2,function(i){
f = (kphaz$strata==i)
data.frame(time=kphaz$time[f],haz=kphaz$haz[f])
})

図示します。

 plot_S =ggplot() +
 geom_line(data=df_S[[2]],aes(x=time,y=mean),size=0.5,linetype=1) +
 geom_ribbon(data=df_S[[2]],aes(x=time,ymin=lower,ymax=upper),alpha=0.3,inherit.aes=F) +
 geom_line(data=df_S[[1]],aes(x=time,y=mean),size=0.5,linetype=2) +
 geom_ribbon(data=df_S[[1]],aes(x=time,ymin=lower,ymax=upper),alpha=0.3,inherit.aes=F)
 plot(plot_S)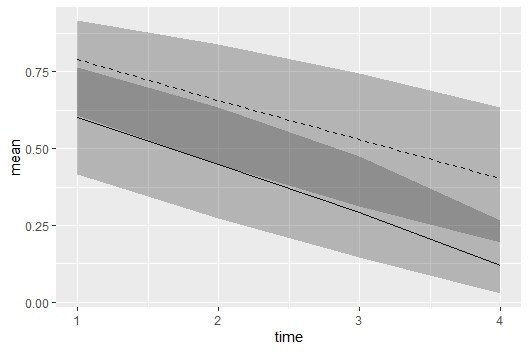

第1日目から差があって広がらないし、狭まらないです。
95%ベイズ信用区間は重なっていて有意差はなさそうです。