分散分析をしてみよう。

前回までのToothGrowthでは、実は歯の長さlenの因子としては栄養の種類supp(OJとVC)、用量(0.5mg、1.0㎎、2.0㎎)の2要因あります。
交互作用と主効果を評価するためには2元配置分散分析が必要です。
まず、栄養の種類と用量に注目して箱ひげ図を作成します。

boxplot(len ~  dose + supp , data=ToothGrowth)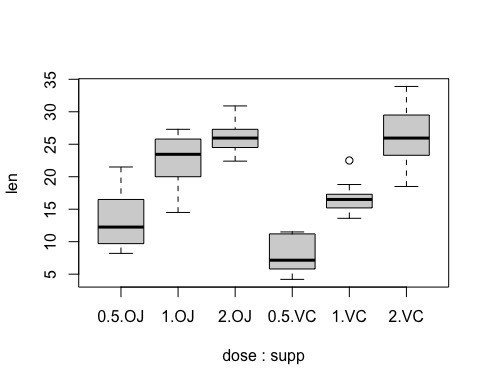

なんとなく、用量には依存していそうです。
引き続き、分散分析aovで評価します。
doseを数値型から因子型に変換して解析しています。

ToothGrowth=transform(data,dose=as.factor(dose))
aov.fit=aov(len ~ supp * dose , data=ToothGrowth)
summary(aov.fit)

Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2

supp:doseでは交互作用を認めます(p=0.022)。
主効果suppもdoseも統計学的有意差あり(それぞれp<0.001、P<0.0001)。
そこで多重比較、今回はTurkey-Kramar法で対比較します。

TukeyHSD(aov.fit)

Tukey multiple comparisons of means
95% family-wise confidence level

Fit: aov(formula = len ~ supp * dose, data = ToothGrowth)

$supp
diff lwr upr p adj
VC-OJ -3.7 -5.579828 -1.820172 0.0002312

$Dose
diff lwr upr p adj
1-0.5 9.130 6.362488 11.897512 0.0000000
2-0.5 15.495 12.727488 18.262512 0.0000000
2-1 6.365 3.597488 9.132512 0.0000027

$`supp:dose`
diff lwr upr p adj
VC:0.5-OJ:0.5 -5.25 -10.048124 -0.4518762 0.0242521
OJ:1-OJ:0.5 9.47 4.671876 14.2681238 0.0000046
VC:1-OJ:0.5 3.54 -1.258124 8.3381238 0.2640208
OJ:2-OJ:0.5 12.83 8.031876 17.6281238 0.0000000
VC:2-OJ:0.5 12.91 8.111876 17.7081238 0.0000000
OJ:1-VC:0.5 14.72 9.921876 19.5181238 0.0000000
VC:1-VC:0.5 8.79 3.991876 13.5881238 0.0000210
OJ:2-VC:0.5 18.08 13.281876 22.8781238 0.0000000
VC:2-VC:0.5 18.16 13.361876 22.9581238 0.0000000
VC:1-OJ:1 -5.93 -10.728124 -1.1318762 0.0073930
OJ:2-OJ:1 3.36 -1.438124 8.1581238 0.3187361
VC:2-OJ:1 3.44 -1.358124 8.2381238 0.2936430
OJ:2-VC:1 9.29 4.491876 14.0881238 0.0000069
VC:2-VC:1 9.37 4.571876 14.1681238 0.0000058
VC:2-OJ:2 0.08 -4.718124 4.8781238 1.0000000

対比較では以上の通りとなっています。
全体の評価としてはOJ群とVC群では比較すると
lenの平均値は統計学的有意差を認めます(p<0.001)。
lenの平均値は各用量で有意差あるようですが、
OJ1.0-OJ2.0では有意差を認めないようです。

すべての組み合わせでは評価すると統計学的有意差を認めないです。
VC:1-OJ:0.5
OJ:2-OJ:1
VC:2-OJ:1
VC:2-OJ:2 

統計学的に解釈すると、分散分析では各群間で全ての水準で等しい=差がないという帰無仮説を否定し、つまりどれかが等しくないと判断し、その後、いわゆる下位検定で多重比較て有意差があるものを探し出すという解析なので煩雑になります。