新型コロナウイルスが無かった場合の2020〜2022年の入園者数をSARIMAモデルで予測して実際の数字と比較してみた。
はじめに
一般財団法人で4年3か月勤務、2022年2月よりAidemyでデータ分析講座を受講。
これまでPythonを用いたプログラミングは未経験。
本記事の概要
とある商業施設における新型コロナウイルスが無かった場合の2020〜2022年の入園者数をSARIMAモデルを使用して予測してみます。
実行環境 Google Colaboratory
使用言語 Python 3.7.13
作成したプログラム
データの呼び出し
まず自前で用意した過去の入園者数のデータを収集し、編集を行いました。エクセルファイルからCSVファイルへ変換しGoogle Driveに保存をします。次に下記のコードを用いてGoogle ColaboratoryからGoogle Driveにマウントをかけcsvファイルを呼び出せるようにします。
from google.colab import drive
drive.mount('/content/drive')ここから実際にファイルを呼び出してみます。
head()を用いて呼び出すと、先頭5行のデータが表示されました。
import pandas as pd
data = pd.read_csv('drive/My Drive/Datasets/visitors_per_month.csv')
data.head()
------------実行結果------------
Month total guests
0 1991-10-01 218379
1 1991-11-01 204012
2 1991-12-01 39823
3 1992-01-01 81747
4 1992-02-01 37355実際の入園者数の変位を見てみる
過去30年の入園者数の変位を実際に出力して確認してみます。
インデックスを年月にする編集を行い、matplotlib.pyplotモジュールを用いて出力をしました。
import pandas as pd
import matplotlib.pyplot as plt
#インデックスの編集
index = pd.date_range("1991-10-01", "2022-04-01", freq = "M")
data.index = index
del data['Month']
#2022年3月31日までのグラフを表示する
plt.figure(figsize=(20,10))
plt.plot(data)
plt.show()
実際のデータを見ると、これまでの入園者数は2020年の新型コロナウイルスに加えて2011年の東日本大震災の影響も受けていることがわかります。今回は東日本大震災の翌年、2012年1月から新型コロナ流行前の2019年12月までの大きな災害等が無かった通常時のデータを用いてモデルに学習をさせます。
データの整理
データセットの不要な行をdrop()を用いて取り除きました。head()とtail()でデータの前後5行ずつを表示して確認します。
#東日本大震災発生の年以前と新型コロナの発生後の年を除き2012〜2019年に絞る
data= data.drop(data.iloc[:243].index)
print(data.head())
data= data.drop(data.iloc[96:].index)
print(data.tail())
------------実行結果------------
total guests
2012-01-31 30553
2012-02-29 13639
2012-03-31 52982
2012-04-30 155146
2012-05-31 262798
total guests
2019-08-31 458981
2019-09-30 95162
2019-10-31 268135
2019-11-30 100190
2019-12-31 31393実際に2012年1月から2019年12月までになっていることが確認できました。
モデルの構築
SARIMAモデルを構築する準備としてモデルで用いる(p, d, q) (sp, sd, sq, s)、7つのパラメーターを情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを記述しました。
import pandas as pd
import itertools
import statsmodels.api as sm
#BIC(ベイズ情報量基準)を用いてSARIMAモデルのパラメーターの最適値を求める
def selectparameter(DATA, s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA, order=param, seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs, results.bic)
except:
continue
return print(parameters[np.argmin(BICs)])
print(selectparameter(data, 12))このコードの実行の結果
[(0, 1, 1), (1, 1, 0, 12), 2104.448430709969]
というパラメーターが得られたので、こちらを用いてモデルを構築していきます。
モデルの構築にはsm.tsa.statespace.SARIMAX(DATA,order=(p, d, q),seasonal_order=(sp, sd, sq, s)).fit()を用います。2018年始から2023年末までの入園者数を予測します。後ほど実際の入園者数とグラフを重ねるため、予測のグラフは赤色にします。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
#モデルの当てはめ
SARIMA_data = sm.tsa.statespace.SARIMAX(data, order = (0, 1, 1), seasonal_order=(1, 1, 0, 12)).fit()
#SARIMAモデルによる予測を行う
pred = SARIMA_data.predict("2018-1-31", "2023-12-31")
plt.plot(pred, color="r")
plt.show()出力結果として下記のグラフが得られました。

続けて元のデータ(2012年始から2019年末まで)との重ね合わせを行います。
import matplotlib.pyplot as plt
#予測の値の重ね合わせ
plt.plot(data)
plt.plot(pred, color="r")
plt.show()出力結果は下記の通りになりました。

2018年と2019年の重なっている部分を見ると、特に2019年が予測に近いように読み取れます。大方の傾向も合っていて、実数に沿っていると言えるのではないのでしょうか?
それでは2020年始から2022年3月末までの新型コロナウイルスが無かった場合の予測入園者数と実際の入園者数を比較していきます。整理前のデータセットを別の変数data1に分けておいて、予測入園者数との重ね合わせを行います。
import matplotlib.pyplot as plt
#予測と実際の数値の重ね合わせ
plt.figure(figsize=(20,10))
plt.grid(True)
plt.title("Numbers of visitors with or without COVID19")
plt.xlabel("Month")
plt.ylabel("Number of Visitors")
plt.plot(data1.index, data1, label="Real")
plt.plot(pred.index, pred, color="r", label="Without COVID19")
plt.legend()
plt.show()得られた出力結果は下記のようになりました。
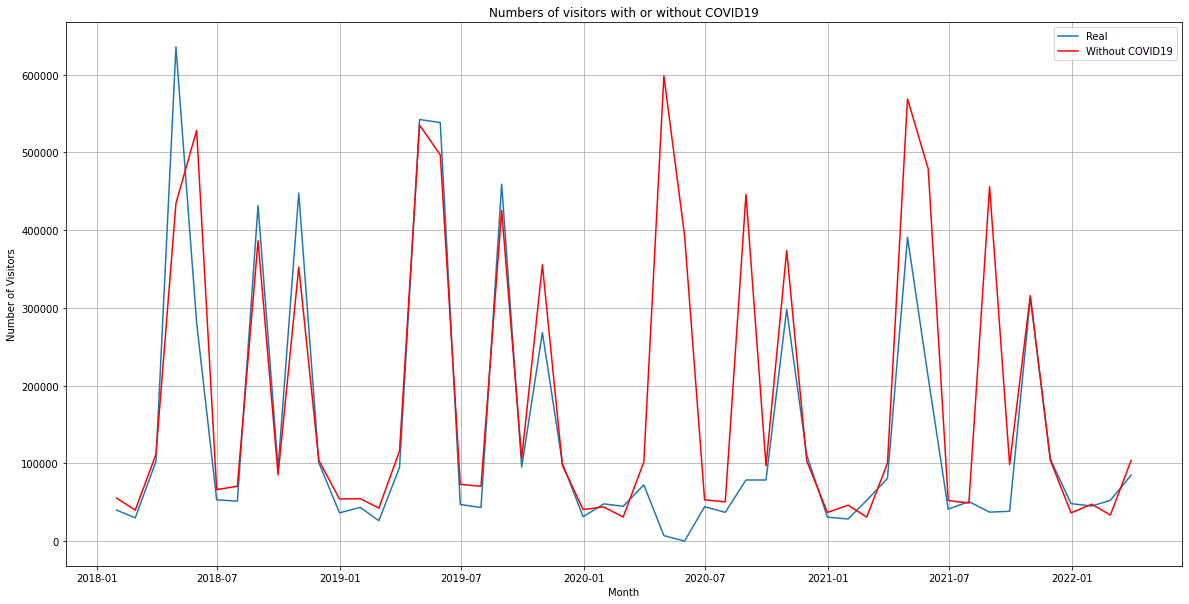
これを見ると2020年の春から夏頃にかけて入園者数の大幅な減が2度ほどあるのが読み取れます。2021年の春には少し回復したと言えますが予測と実際の差が15万人ほどあり、夏には40万人ほどの減となっています。新型コロナウイルスの発生から1年以上経過して尚、影響を引きずっていたことがわかりました。
今後の活用
今後は天気や気温の変化などデータの種類を増やしてより複雑なモデルでの解析を行っていければと思います。
おわりに
今回は扱うデータの種類も少なかったため、簡単な分析となりましたが、今後は実力の伸びと共に徐々にグレードアップしていきたいと思っております。
最後までお読みいただきありがとうございました。
参考文献
今回はAidemy教材から、「時系列解析Ⅰ(統計学的モデル)」を参考に作成しました。
https://premium.aidemy.jp/courses/5060
この記事が気に入ったらサポートをしてみませんか?
