【ラビットチャレンジ】応用数学レポート

一部「超AI入門講座」で学習した内容も含まれるが復習をかねてまとめていく。

◆第1章　線形代数

○スカラー
＋−×÷の演算が可能

○ベクトル
「大きさ」「向き」をもつ

○行列
ベクトルの変換に使う

○単位行列
かけてもかけられても相手が変化しない「1」のような行列

○逆行列
まるで逆数のような働きをする。
掃き出し法という求め方がある。

○固有値と固有ベクトル
ある行列Aに対して以下のような特殊なベクトルと右辺の係数

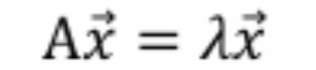
○固有値分解
以下は具体例である

◆第2章　確率•統計

○頻度確率(客観確率)
(例)「10本のうち1本だけ当たりのくじを引いて、当選する確率を調べたところ10%であった」という事実

○ベイズ確率(主観確率)
(例)「あなたは10%の確率でインフルエンザです」という医師の診断

○ 確率変数
事象と結び付けられた数値

○確率分布
事象の発生する確率の分布、離散値であれば表に示せる。

○期待値
その分布における確率変数の「平均の値」もしくは「発生しそうな値」

○分散
データの散らばり具合

○共分散
「二組の対応するデータ」間の関係を表す数値

◆第3章　情報理論
○自己情報量
logの底を2にしてbitで表すことが多い

○シャノンエントロピー
自己情報量の期待値、情報エントロピーなどともいう。

○カルバック・ライブラー　ダイバージェンス
同じ事象、確率変数における異なる確率分布の違いを表す。

○交差エントロピー
クロスエントロピーともいう。2つの確率分布の間に定義される尺度。カルバック・ライブラー　ダイバージェンスの一部を取り出したもの。

★