
サイエンス・セミナー
サイエンス・セミナー: 近隣の「理科が好きな」中、高校生を対象に、大学を夏休みの1日、解放して「科学的な遊び」をする「大学・研究紹介の一企画」です。さまざまな研究分野があります。自分の好きな分野の先生の所のブースで討論します。以下は、プログラミング、画像計算ブースの例です。
T: 複素数、漸化式を学習しましたか?
複素数Z(n)の漸化式: Z(n+1)=A*Z(n)**2+B*Z(n)+C、A,B,Cは複素定数、はどういう複素平面上の操作(軌跡)を示していますか?
S1: B*Z(n) 部分で拡大・縮小;Z(n)**2 部で回転;全体で平行移動を含むアフィン変換です。平面上の幾何的操作の全部です。
S2: n→∞(十分大きい自然数) とすれば集合{Z(i)}は離散図形です。
0=A*Z(n)**2+{B*Z(n)-Z(n+1)}+C, 0=A*x**2+x(B-1)+C, 根{x}は添字nによらないので停留点です。集合{Z(i)}は2停留点{x0,x1}を有する離散点の図形です。
Z(0)≠x0 or x1ならば「停留点へ収束する」か「2停留点を巡回するか発散する」でしょう。
S3: Z(0)が分布{Z(0)+δ}, δは微小数の2次元集合(複素数)ならばδ集合の発散図が描かれるでしょう。
S4: n→∞操作でmod(n,2~), 2~は2以上の自然数、として剰余関数mod()の値で点の色を変えれば色彩図形です。
S5: 0=A*Z(n)**2+B*Z(n)+{C-Z(n+1)}, 0=A*x**2+B*x+C', 根{x}は{Z(n-1)}です。
n→ -∞操作では一点Z(0)から出発しても無限点の図形です。
-∞<n<∞の操作では無限点が1点に収斂し、再度、無限に発散する可能性があります。
T2: n→∞ ではZ(-n)の数が無限に多くなるが、Z(+n)では1個です。数学に粒子数という概念は無いですが、物理的な考え方なら、粒子~エネルギーだから、粒子数が多い~粒子のプロット濃度を下げる、とでもするのかな。
そうするとn→-∞ではn=-8ぐらいで1/256の濃度になり、事実上「それ以前」が「無になる」。
nを「時間のような軸の目盛」と考えれば「過去には、長く遡れない」ということだな。少なくとも有限。
複素漸化式は離散的な状態記述式です。物理の運動方程式は連続無限の記述式なので「時間は過去には遡れない」のは当然です。
いろいろ異論があると思うけど、このように考えると「興味深い式」です。
T3: Z(n)の近傍{Z(n)+δ}を考えてみます。
Z(n+1)=A*{Z(n)+δ}**2+B*{Z(n)+δ}+C =[AZ(n)**+BZ(n)+C] + [2AZ(n)+B]δ
第1項はZ(n)の式のママ。第2項が摂動δの影響です。ゆえに2AZ(n)+B=0ならば、摂動の影響が極小で集積点が存在しうる。
T4: 実際に数値を決めて計算します。
(Z-0.5)**2=Z**2-Z+0.25, Z(n+1)=Z(n)**2+0.25, ゆえにA=(1,0),B=0,C=0.25,
この漸化式で{Z(0)+δ(i)}の軌跡を描きます。n<125000とします。
δ(0)=0, {δ(i), i=1,2,...7}={|Z(0)|/10}{cos(2π(i-1)/7),sin(2π(i-1)/7)}とします。
Z(0)=(0.1,0.1)の軌跡は重根(0.5,0)に収斂する。

<rootConv.jpg>
(Z-0.1)(Z+0.1)=Z**2-0.01; Z(n+1)=Z(n)**2+Z(n)-0.01;
A=1, B=1, C=-0.01; Z(0)=(0.01,0.01)で2根(-0.1,0),(+0.1,0)へ収束します。
Z(0)=(0.1,0.01)でも同じ、2根(-0.1,0),(+0.1,0)へ収束します。
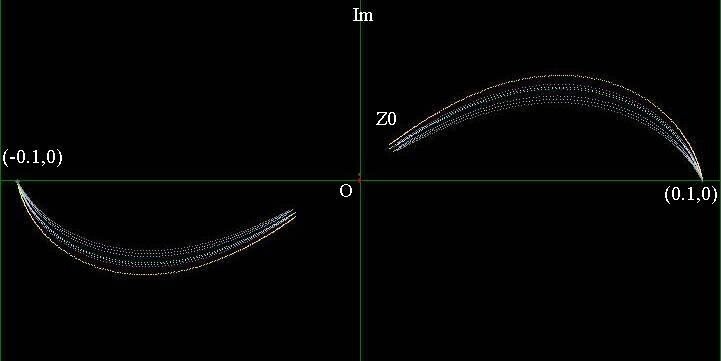
<rootConv2.jpg>

<rootConv3.jpg>
これで、Z(n+1)=A*Z(n)**2+B*Z(n)+Cが描く軌跡の制御ができます。
みなさん、プログラミングしてみましょう。
S6: 0=(Z-1)(Z-i)=Z**2-iZ-Z+i; Z(n+1)=Z(n)**2-iZ(n)+i;
A=1, B=(0,-1), C=(0,1), Z(0)=0で計算してみます。
すぐ収束してダメですね。Z(0)=(0.5,0.5)では、

<rootConv4.jpg> 打ち上げ花火のようです。根iに収束しています。
Z(0)=(0.9,0.5)は即、発散でダメ。
Z(0)=(0.99,0) 根iに収束、根1には収束しない、鞍点です。

<rootConv5.jpg>
T5: シフト・レジスタ{Z(n)→Z(n+1)→Z(n+2)→...}という操作を導入します。
Z(n+2)=A*Z(n+1)**2+B*Z(n)+C という漸化式が考えられます。
その停留点は0=A*Z**2+(B-1)*Z+Cの根です。
前の漸化式とは違い、初期値が2個です。Z(1)を決めなければなりません。
常識的にはZ(1)=conj{Z(0)}でしょう。ということは、実軸対称という「何か」を導入したのです。根に収斂する可能性はありますが、その途中では前の漸化式とは違うでしょう。
試行します。
A=(1,0),B=0,C=0.25,Z(0)=(0.1,0.1)の軌跡は重根(0.5,0)に収斂する。

<root2Conv.jpg>
A=1, B=1, C=-0.01; Z(0)=(0.01,0.01)では根へ収束せず、発散*します。
*発散: コンピュータで計算するとき、あまりに大きな数は計算できません。ですのでAbs{Z(i)}>2となったとき計算を止めます。i=1桁の自然数、という場合は「ほとんど図が描けません」。i=数千ならば「点描図」ですが描けます。i=数万ならば「線」が描けます。プログラムではiteration=125000でZ(i)がどの値であろうとも止めます。
ここで一寸、脱線します。
Z(n+1)**2 +D*Z(n+1)=A*Z(n)**2+B*Z(n)+Cという漸化式を何故やらないのか、分かりますか?右辺は計算すれば複素数の値になる、これをEとします。すると、Z(n+1)**2 +D*Z(n+1)-E=0 の2根がZ(n+1)です。
そうです、Z(n)が1点でもn→∞で{Z(i)}集合は無限集合になります。だからコンピュータでは「大きなn」まで計算できません。
すなわち複素漸化式全体の図形集合は、限られた{n}の範囲でしか見通せない、ことが分かります。
プログラミングでは数理物理学の式が記述する世界よりも「狭い世界」しか到達できません。
Z(0)=(0.001,0)、2300~4500 iterationsで発散します。プロット図は、

<root2Conv2.jpg>です。{Re,Im)=±0.366(図では0.183ですが2倍してください。以下同様)の平面を表示。
Z(0)=(-0.09,0)ならIm部が0なら2根へ収束、Im部≠0なら発散します。プロット図は、

<root2Conv2c.jpg>です。{Re,Im)=±1.657の平面を表示。
Z(n+2)=A*Z(n+1)**2+B*Z(n)+Cが描く軌跡の制御ができます。根への収束半径は小さいです。みなさん、プログラミングしてみましょう。
S7: A=1, B=(0,-1), C=(0,1), Z(0)=0で計算してみます。
すぐO=(0,0)に収束してダメですね。
Z(0)=(0.5,0.5)ではiteration=5~7で発散です。
Z(0)=(0,0.9)ではiteration=2~3で発散です。
T6: Z(1)=conj(Z(0))がじゃましている。
Z(0)=(0.9,0)はiteration=11までで発散、根(1,0)は鞍点ですね。
収斂しないようだから(Z-0.01)(Z-0.01i)=0にしましょう。
要するにn→∞でZ**n→0にしないと発散してしまうわけ。だから根は原点Oの近くにする。
根i=(0,0.01i)と根1=(0.01,0)でいきます。
ゆえにA=1, B=(0.99,-0.01), C=(0,0.0001)。
Z(0)=(0.001,0.001)で根iに収斂します。2軌跡はZ(0),Z(1)があるからですね。
Z(0)=(0.001,-0.001)でも根iに収斂します。軌跡が変化します。当然ですね。

<root2Conv3.jpg> {Re,Im)=±0.022の平面を表示。
Z(0)=(0.01,7.e-3)でも根iに収斂します。鞍点(0.01,0)付近の反発軌跡が顕著。

<root2Conv4.jpg> {Re,Im)=±0.0556の平面を表示。
T6: 色というものについて:
物理的には光子のエネルギーです。光子は波の性質もあるので、「光の」波長と色が対応します。
ここの画像には色がついていますが、色と物理事象との対応はありません。
色は初期値Z(0)が違うことを表しています。
その彩色法について書きます。
色をRGB3原色の[0,255]区間の整数値で表現します。
ポジ8色{赤、黄、緑、シアン、 青、マゼンタ、暗い灰、明い灰}です。
{R(j),j=1,...8}={200,100,0,0, 0,100,67,110}
{G(j)}={0,100,200,100, 0,0,67,110}
{B(j)}={0, 0, 0, 100, 200,100,67,110}
ネガ8色=255-ポジ色 とします。今までの画像中の各点はネガ8色です。
{Z(0)+δ}のδ=0の中心点の軌跡はNega{R(1),G(1),B(1)}={100,255,255}です。
灰色がかったシアンです。δは中心Z(0)の微小円、半径=|Z(0)|/10の円周上の7等分点です。
中心点を入れて全部で8点あるので、8色で点描します。
色の順序: 灰シアン、灰青、灰マゼンタ、灰赤; 灰黄、灰緑、明い灰、暗い灰。
T8: 収束半径について調べます。
>>T4: (Z-0.1)(Z+0.1)=Z**2-0.01; Z(n+1)=Z(n)**2+Z(n)-0.01;
A=1, B=1, C=-0.01; Z(0)=(0.01,0.01)で2根(-0.1,0),(+0.1,0)へ収束します。
2根を中心にして±2の範囲、Re/Im軸があるから(±2,±2)の平面内の全点をZ(0)としてiterationします。計算量が大なのでiteration<10**4にします。結果の2画像(モノクロ):


<Root01m01.gif/Root01p01.gif>
白い部分がiteration=10**4まで|(Z(i)|>2にならない範囲です。
黒い部分がiteration=10**4以下で|(Z(i)|>2となった範囲です。
プログラムでは|(Z(i)|>2となったとき、(iteration)**0.5の値を0.5乗して記憶し、平面内の全ての値を[0,255]の範囲にスケールして表示しています。「0.5乗」で小値を強調しています。
白い円状の形の輪郭が「0.5乗しても」はっきりしています。閾値が存在する、ように見えます。この2画像から「収束半径」という言葉が的外れでない、ことが分かるでしょう。
重根のときを調べます。
>>T4: (Z-0.5)**2=Z**2-Z+0.25, Z(n+1)=Z(n)**2+0.25, ゆえにA=(1,0),B=0,C=0.25
結果:

<Root05.gif>
白・黒の意味は同じです。白い部分の輪郭がフラクタルのようですね。
実・虚の対称性も崩れている。
>>S6: 0=(Z-1)(Z-i)=Z**2-iZ-Z+i; Z(n+1)=Z(n)**2-iZ(n)+i;
A=1, B=(0,-1), C=(0,1) では?


<Root6re.gif><Root6im.gif>
根(1,0)へ収束する領域もあります。ただし根の近傍→他の根という収斂です。
T9: 図<Root6re.gif>の輪郭について調べます。
iteration=10**4では輪郭は明確でした。iteration=10**6かつ実軸上を詳細に調べます。
結果:
test#: Re{Z(i)} Im{Z(i)} iter#
----------------------------------------------------
25: 1.24272 0.111022E-15 1000000
26: 1.25243 0.111022E-15 9 ←新しく見つかったGap、発散領域
27: 1.26214 0.111022E-15 10
28: 1.27184 0.111022E-15 1000000
29: 1.28155 0.111022E-15 1000000
30: 1.29126 0.111022E-15 100000
-----------------------------------------------------
39: 1.37864 0.111022E-15 1000000
40: 1.38835 0.111022E-15 1000000 ←ココがRoot6re.gifの輪郭
41: 1.39806 0.111022E-15 7
42: 1.40777 0.111022E-15 6
43: 1.41748 0.111022E-15 4 以下ずっと1ケタの数=発散
----------------------------------------------------
結論: 収束半径内部に発散領域が分散しています。
軌跡が根に漸近していっても、この発散域に入ると「突如、遠方に弾かれる」ことがあり得ます。
漸近→遠方→再び漸近→繰り返し、という間欠泉のような軌跡の動きがあり得ます。
T10: Z(n+2)=A*Z(n+1)**2+B*Z(n)+C の収束半径を求めます。
A=1,B=0,C=0.25, 重根(0.5,0)周辺のiteration=80kの半径です。

<Root05_2nd.gif>
もはや半径とは呼べない形状で、輪郭も切れ込み、内部の発散点、周辺のもやのような領域,、飛地といろいろ存在します。
シフト・レジスタ{Z(n)→Z(n+1)→Z(n+2)→...}操作をZ(n+3)まで伸ばすとどうなるのでしょうか?
S8: 収束域の輪郭が明瞭で無くなります。Z(2)=-Z(0), Z(1)=conj{Z(0)}として計算します。輪郭外を0.5乗より強調するためにLn()とします。

<Root05_3rd.gif>
予測どおりです。2nd order iterationとずいぶん違います。Z(n+4)まで伸ばします。Z(2)=-Z(0), Z(1)=conj{Z(0)},Z(3)=conj{Z(2)}として計算します。
輪郭外を強調するためにLn()とします。これで初期値4個の対称性については完成です。

<Root05_4th.gif>
S9: 3rd. order iteration: Z(n+2)=A*Z(n+1)**2+B*Z(n)+C,
Z(2)=-Z(0), Z(1)=conj{Z(0)}のA値を同心円の円周上で変えると画像が変わります。収束半径が~0でなので。モアレも見えます。

<root300div0.jpg>

<root300div1.jpg>

<root300div2.jpg>
---- 三次元編 ----
T11: 今まで複素数について調べてきました。複素数は実(Re)、虚(Im)の2次元の世界です。それを3次元にしたいですね。
複素数(complex)以上の次元を有する数に四元数(よんげんすう、quarternion, Q)があります。
Q=(a+bi)*1+(c+di)*j =a+bi+cj+dk, k=ij で定義される数です。
ここでi,j,kは、i**2=-1, j**2=-1, k**2=-1; ij=k, ji=-k; jk=i, kj=-i; ki=j, ik=-j,
という関係にある虚数単位です。
Qの世界では-1の平方根は無限にあります。そして乗算の交換則が成立しません。a*b≠b*a です。加算の交換則は存在します。a+b=b+a.
このような数で自然界の法則を記述できるか?ということですが。。。
大学で学ぶ物理学の範囲では、複素数までで十分なので、四元数は不要でした。
今までの私の経験では、「3次元の回転操作」がこの数ですと「簡便な式」になる、という利点がありました。
Q=a+(bi+cj+dk)=s+v; s=scalar, v=3 dimensional vector です。
四元数は3次元ベクトルに1つのスカラー量"s"が付いたもの、と見ることができます。
化学の世界では、炭素原子に4個の異なる置換基が付いた化合物は、2種類の光学活性体が出来ます。両者は偏光性が異なり、生物学的性質も異なります。
これは v=(b*i,c*j,d*k)なる3次元ベクトルでは、自然を記述するための「何かが不足」していることを示します。その不足分が"s"という量だと思います。
私は四元数は見かけは4次元ですが、3次元の数と考えています。
ところで、四元数は複数の表現型があって、ここで示すのはHamiltonの提唱した形です。
こういう状況ですので、四元数の漸化式を調べてみるのも面白いかな、と考えています。
Qの二次方程式 0=(Q+A)(Q+B) から演繹します。
ここでA,B,0はQの定数とゼロです。
0=Q**2+A*Q+Q*B+A*B,
Q(n+1)=Q(n)**2 +A*Q(n)+Q(n)*B+Q(n) +A*B, initial Q(0),
が1st. orderのiterationです。根は -A and -B です。
Qの計算ライブラリーはありますが、ここでは、自分でcodingします。
私はadd, multiply, inverse, conj, abs,...を作成しました。
例:
Subroutine Q_mult(s,u,v,w, s1,u1,v1,w1,s2,u2,v2,w2)
implicit real*8 (a-h,o-z) ! multiply
s=s1*s2 -u1*u2 -v1*v2 -w1*w2
u=s1*u2 +u1*s2 +v1*w2 -w1*v2
v=s1*v2 -u1*w2 +v1*s2 +w1*u2
w=s1*w2 +u1*v2 -v1*u2 +w1*s2
Return
End
s軸上の重根0.5で計算してみます。
A=B=(-0.5, 0,0,0), Q(0)=(0.1, 0.1, 0.1, 0.1), iter<10000 の結果です。

<Q05.gif> (s,i)と(j,k)の平面を重ねてあります。描画範囲は±0.51です。
根0.5に収束しました。
原点Oから45度の方向の直線は(j,k)要素が→0へ収束している軌跡です。
A=(0.01, 0,0,0), B=(-0.01, 0,0,0), Q(0)=(1.e-3, 1.e-3, 1.e-3, 1.e-3), iter=10k,
Q(10k)=(-0.01, 0,0,0):=root A です。
Q(0)=(-1.e-3, 1.e-3, 1.e-3, 1.e-3) ではQ(10k)=(-0.01, 0,0,0):=root A です。
root Bへは収束しません。
Q(0)=(1.e-2, 1.e-4, 1.e-4, 1.e-4), Q(10k)=(-0.01, 0,0,0):=root A です。
root Bへは収束しません。{Q(i)}の平面(s,i)上の軌跡はroot Bから半円状にroot Aへ動いています。

<Q01p2.gif> scale=[-0.11,0.11], (s,i) & (j,k)平面
Q(0)=(1.e-2, 0,0,0):=root B, Q(10k)=(0.01, 0,0,0):=root B です。
root Bは確かに根ですが、鞍点です。
A=(0, 0.01, 0,0), B=(0, -0.01, 0,0), Q(0)=(1.e-3, 1.e-2, 1.e-3, 1.e-3), iter=10k,
は次第に発散する偏心軌跡です。

<Q01ip.gif> scale=0.015 明るい軌跡が(s,i)平面、暗い軌跡が(j,k)平面です。
Q(0)=(1.e-3, -1.e-2, 1.e-3, 1.e-3), iter=10k も次第に発散する偏心軌跡です。

<Q01im.gif> scale=0.015 明るい軌跡が(s,i)平面、暗い軌跡が(j,k)平面です。
根そのもの Q(0)=(0, -1.e-2, 0,0), iter=10k ならば軌跡は、動かない点です。根からわずかに動くと、Q(0)=(0, -0.99e-2, 1.e-4,0), iter=10k 次第に発散する偏心螺旋軌跡です。

<Q01ij.gif> scale=0.35, この2根は鞍点です。
T12: j,k要素を0として、(s,i)平面の収束半径を計算します。
A=(-0.01,0,0,0),B=(0.01,0,0,0), Q(0)=[-2,2]の範囲を図示します。

<Q01rad.gif> scale=±2, iteation<1k, Ln()
こうして見ると、根(0.01,0,0,0)の周囲は発散領域で、根の所だけが停留点です。A,Bを交換してもQ01rad.gif図は変わりません(加算では交換則がある)。根周辺を拡大します。[0,0.02]の範囲を図示します。

<Q01rad.gif> scale=0.02, iteation<1k, Ln()
根の位置から拡散領域がs軸方向に3角形に延びています。
3角形の稜線は直線ではなく、ノコギリの歯のようです。おそらくフラクタルでしょう。i軸方向にずれると根(-0.01,0,0,0)へ収斂する領域(白い部分)が広がっています。
S10: <Q01rad.gif>で原点対称でないのは何故ですか?
T13: 0=(Q+A)*(Q+B)から両辺に+Qとしたでしょう。それで根A,Bの対称性からs軸の負方向にずれたのです。
A=(0, 0.01, 0,0), B=(0, -0.01, 0,0), Q(0)=(1.e-3, 1.e-2, 1.e-3, 1.e-3), iter=10k,
は次第に発散する偏心軌跡でした。この根A,Bの収束半径を求めます。

<Q01radIMG.gif> scale=[-2,2], iter<40k, Ln()
収束半径が灰色になっています。すなわち収束ではなく、発散です。ごく一部に白に近い所があります。そこは集積点です。
A=(0,0, 0.01,0), B=(0,0, -0.01,0), iter<10kの収束半径は<Q01radIMG.gif>と同じです。
A=(0,0, 0,0.01), B=(0,0, 0,-0.01), iter<10kの収束半径は<Q01radIMG.gif>と同じです。
ゆえに虚軸i,j,kの等価性が計算でも現れ、プログラムの正常性が確認できます。
A=(0,0.01, 0.01,0.01), B=(0,-0.01, -0.01,-0.01), iter<10kの収束半径は<Q01radIMG.gif>と同じです。
A=(0.01,0.01, 0.01,0.01), B=(-0.01,-0.01, -0.01,-0.01), iter<10kの収束半径は<Q01rad.gif>と同じです。
A=(0.01,-0.01, -0.01,-0.01), B=(-0.01,0.01, 0.01,0.01), iter<10kの収束半径は<Q01rad.gif>と同じです。
A=(0,0, 0.1,-0.1), B=(0,0, -0.1,0.1), iter<4kの収束半径は(s,i)平面で、

<QjkRad.gif> scale=1, bias=-0.5(原点Oがs軸上で-0.5)です。Ln()処理あり。ほぼ全面で発散です。
A=(0,-0.4, 0.1,0), B=(0,0.1, -0.4,0), iter<10kの収束半径は(s,i)平面で、

<Qij_us.gif> scale=1, bias=(-0.5,+0.5) (原点Oがs軸上で-0.5,i軸上で+0.5)です。Ln()処理あり。 iter<20kの拡大(s,i)平面図です。

<Qij_vs.gif> scale=0.5, bias=(-0.25,+0.75), Ln()処理あり。
フラクタル性のある収束半径です。
T14: 四元数を Q=s+(i,j,k):=scalar+(vector, 3D)として、iteration: Q(n+1)=Q(n)**2+A*Q(n)+Q(n)*B+A*B を考えていくことにします。
根 A=(0,0.01, 0.01,0.01), B=(0,-0.01, -0.01,-0.01), iter<2k のときの収束半径です。

<QijkRad.png> scale=[-0.2,0.2].
根Bの近傍の Q(0)=(0,-0.01, -0.00999, -0.01001)ではiter=39kで原点からの距離が2を超えます。その軌跡をscale=[-0.035,0.035]で描きます。

<Q011.png> 赤が(i,j)平面、緑点が(j,k)平面です。原点O=(0,0)は2平面で共通。R+Gは黄色です。根の位置の微小変位がiterationで拡大して無限に発散していくことが分かります。赤と緑に分岐した所で発散の方向が曲がっています。
根の近傍点の軌跡像を描きます。
Q(0)の近くの集合{Q(0)+δ}を定義して、 δをs,i,j,k軸方向に計8点を採用して、±|Q(0)|/100とします。そして、(i,j),(i,k),(j,k)の3平面で{Q(i)}点を、R=200,G=150,B=170、で点描します。
scale=[-0.025,+0.025]にして、3平面を重ね合わせます。
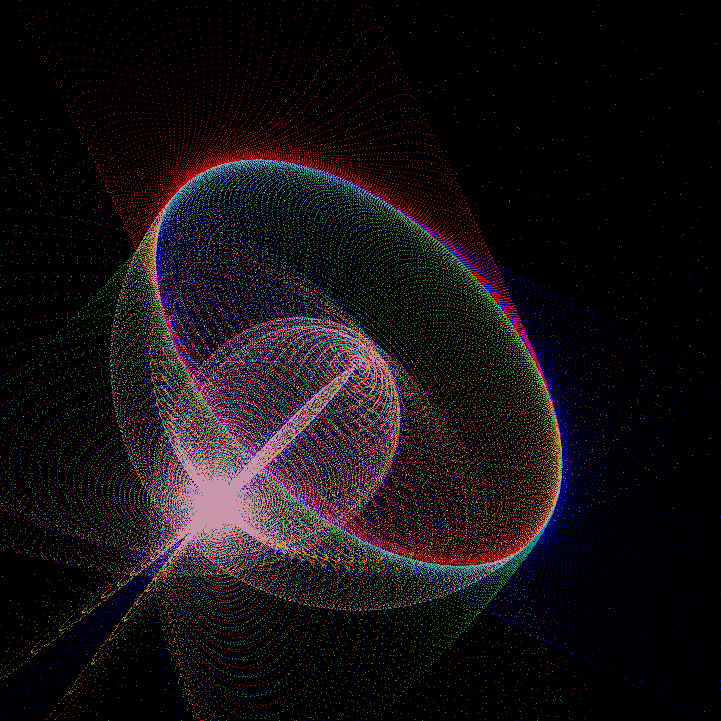
<Q011x.png> 座標軸を消しました。
根Bの近傍の Q(0)=(0,-0.00999, -0.00999, -0.00999)ではiter=12kで原点からの距離が2を超えます。集合{Q(0)+δ}をscale=[-0.07,+0.07]で3平面を重ね合わせた図です。

<Q012.png> 45度方向にジェットが見えます。色は薄紫なので3平面にそれがあります。
>>A=(0,0.01, 0.01,0.01), B=(0,-0.01, -0.01,-0.01), iter<2k のときの収束半径
<QijkRad.png> scale=[-0.2,0.2] (既出)の楕円周上の点は発散点(iter~2k)です。直ぐに発散するのではなくQ(0)の周辺を2000回程度巡回して発散する軌跡です。それを{Q(0)+δ}, δ=±|Q(0)|/10**5で、点描数を多くして描きます。
Q(0)=(0,-0.0544444, 0.14,0)です。

<Q013.png> scale=[-0.14,+0.14]
図から軌跡はQ(0)と原点の周りを巡回しています。
Q(0)のようなiter#が数千の点を集積点と呼びます。集積点の周りのQ(0)には興味深い像は無いようです。
Q(0)=(-0.001,-0.01, -0.01,-0.01), δ=±|Q(0)|/100, scale=[-0.015,+0.015]軌跡です。

<Q015.png> R=(i,j),G=(j,k),B=(s,k)の3平面を重ねました。
---- 7次元編 ----
T15: 今まで四元数について調べてきました。実(s)、虚(i,j,k)の4次元の世界です。それを8次元にします。四元数の拡張は八元数(O, Octonion)です。
Cayley-Dickson constructionに従って、2つの四元数a,bを使い、O=(a,b)=(s,i,j,k; s2,i2,j2,k2)です。sが実部、{i,j,k, s2,i2,j2,k2}の7虚部の数で、記述する空間は七次元です。
大学ではベクトル解析という流体記述のための物理を学びます。そこで3次元空間の連続体方程式、移流拡散方程式を学習します。そのとき渦場rot演算子という3次元の演算子を学習します。この演算子の次元拡張形は7次元です(4次元ではありません)。
私たちは3次元での流体を見ています(水や空気)が、その拡張は7次元でしょう。それに時間の次元が追加されて、8次元が「物理学を構成できる世界」でしょう。
T16: 絶対値は ||O||=sqrt(s*s+i*i+j*j+......k2*k2)です。実数です。
8要素数であっても絶対値はスカラーの実数(0以上の正数)です。
加算は各要素の加算です。乗算は、O*O2=(a,b)(c,d)=(ac-~db, da+b~c)です。~は共役をとること。~d=conj(d)です。
逆数は O**-1=~O/||O||です。四元数と同じ。
八元数ライブラリーは無いでしょうから自作します。四元数ライブラリーを利用します。
八元数のiterationは四元数と同じに、
O(n+1)=O(n)**2 +{O(n)+A*O(n)+O(n)*B} +A*B,
とします。この巡回式で、
O(0)s -1.0d-2
O(0)i -1.0d-2
O(0)j -1.0d-2
O(0)k -1.0d-2
O(0)s2 1.d-2
O(0)i2 1.d-2
O(0)j2 1.d-2
O(0)k2 1.d-2
As 1.0d-2
Ai 1.0d-2
Aj 1.0d-2
Ak 1.0d-2
As2 1.0d-2
Ai2 1.0d-2
Aj2 1.0d-2
Ak2 1.0d-2
Bs 1.0d-2
Bi 1.0d-2
Bj 1.0d-2
Bk 1.0d-2
Bs2 -1.0d-2
Bi2 -1.0d-2
Bj2 -1.0d-2
Bk2 -1.0d-2
このO(0)は、O(0)≠A, O(0)≠Bでも、iter=10kで、O(0) → O(10k)=O(0)で、停留点です。
O(0)s2 =O(0)i2 =O(0)j2 =O(0)k2=ε,
ε=0 iter<85; ε=1.d-4 iter<85;
ε=1.d-3 iter<244; ε=2.d-3 iter<557; ε=4.d-3 iter<1187; ε=8.d-3 iter<2758;
ε=9.d-3 iter<3699; ε=9.9d-3 iter<6685; でした。四元数のような収束半径値の「分布」が存在します。
軌跡の点描図を示します。
--- Table 1 ---
O(0)s -1.0d-2
O(0)i -0.99d-2
O(0)j -0.98d-2
O(0)k -0.97d-2
O(0)s2 10.d-3
O(0)i2 9.90d-3
O(0)j2 9.80d-3
O(0)k2 9.70d-3
------------------
としたとき、iter<6845で||Q(i)||>20(10倍にしました)です。
R=(s,i),G=(i,j),B=(j,k), R=(s2,i2),G=(i2,j2),B=(j2,k2)の6平面を重ねた図,
R=(s,s2),G=(i,i2),B=(j,j2)の3平面を重ねた図、


<O01.png>, <O02.png> ともにscale=[-0.0225,+0.0225]
O(n+1)=O(n)**2 +{O(n)+A*O(n)+O(n)*B} +A*B, |O(i)|<20の収束半径を計算します。iter<1kです。scale=[-0.1,+0.1] 中心点はO(0) in Table 1です。

<O_si01.png> (s,i) plain

<O_ji01.png> (j,i) plain*

<O_ss201.png> (s,s2) plain

<O_w2i01.png> (w2,i) plain*
明暗輝度は[max,min]を[255,0]に自動調整しています。
*印の図では、明瞭な楕円周が描かれていますが、値の差は小さく、周上の点は集積点です。
--- 対称性 ---
T17: 対称という言葉は、図形から来ているんでしょう。
三角形があるとします。その大きさに依らない「性質」を考えると「対称性」です。では、巡回式に対称性はあるか?
複素数なら 0=(Z+A)(Z+B), Z(n+1)=Z(n)**2+{(A+B)*Z(n)+Z(n)}+A*B
でA,Bを交換しても対称。四元数式、0=(Q+A)(Q+B) これは対称ではなく、
0=(Q+A)(Q+B) +(Q+B)(Q+A) です。
0=Q(n)**2+A*Q(n)+Q(n)*B+A*B +Q(n)**2+Q(n)*A+B*Q(n)+B*A,
右辺: 2*Q(n)**2 +Q(n)+{A*Q(n)+Q(n)*A}+{B*Q(n)+Q(n)*B}+(A*B+B*A),
これが対称漸化式です。
この式を2 iterations:
Q(n+1)=Q(n)**2+Q(n)+A*Q(n)+Q(n)*B+A*B,........trace0
Q(n+1)=Q(n)**2+Q(n)+Q(n)*A+B*Q(n)+B*A,........trace1
で書くと、2軌跡です。
A=(0.1,0.1, 0.1,0.1), B=(0.05,-0.1, -0.1,-0.1), Bsだけを0.1→0.05として実部の対称性を崩しています。A=Bなら<QjkRad.gif>類似の画像です。
iteration<2k, scale=[-1.5,1.5]としてtrace0の(s,i)平面の収束半径(分布)図をしめします。

<QR1si.png> trace1の収束半径図(略)も見かけは同じです。
両者の差分図です。

<QBsi.png>
分布図が大体同様なのは理解できますが、差分図が離散的であるのは、traceが段々離れていくのでは無いことを表しています。
応用: 実部の対称性の崩し方によって様々なフラクタル図形が描けます。



<Q041x.png, Q040x.png,Q039x.png>
それぞれ、B=(0.041,-0.1, -0.1,-0.1), B=(0.04,-0.1, -0.1,-0.1), B=(0.039,-0.1, -0.1,-0.1) に対応します。iter<2500, scale=[-0.85,0.85], bias(s)=-0.55, bias(i)=0.35。
T18: 八元数式、0=(O+A)(O+B) 対称ではないですが、 これから演繹される巡回式、O(n+1)=O(n)**2+O(n)+A*O(n)+O(n)*B+A*B,
はO()=-A, -Bで停留します。その近傍ではどうなるか計算しました。
根B=(s,i,j,k; s2,i2,j2,k2)=(-0.01,0.01,0.01,0.01; 0,0,0,0):
δ(s2)=10**-3, iter<17787,
δ(s2)=10**-4, iter<29401,
δ(s2)=10**-5, iter<40830,
δ(s2)=10**-6, iter<52625,
δ(s2)=10**-7, iter<63878,
---
δ(i2)=10**-3, iter<17787,
δ(i2)=10**-4, iter<29401,
---
δ(j2)=10**-3, iter<17787,
δ(k2)=10**-3, iter<17787,
虚部の微小変化δの対称性があります。八元数ライブラリは対称性について正常です。
T19: 2 iterationsが近接の2Q(0)から8次元空間をn→∞に進むと、2 tracesはモアレを生じます。iterationの軌跡は点ですが、波ではありません。でも一見、モアレが見える。眼の錯覚か、計算機の画像処理でreal→integerなる処理が入るので、切り捨てが起こる。それが空間内で等間隔で起こるから、一種のメッシュとなる。それでモアレになる。
計算例:
Iteration 0: O(n+1)=O(n)**2+O(n)+A*O(n)+O(n)*B+A*B,
O(0)=(-0.01,0.01, 0.01,0.01, 0,+0.001, 0,0),
Iteration 1: O'(n+1)=O'(n)**2+O'(n)+O'(n)*A+B*O'(n)+B*A,
O'(0)=(-0.01,0.01, 0.01,0.01, 0,0, +0.001, 0).

<slit_si.jpg> (s,i) plain, scale=(-0.17,0.17), iter<17787, R=iter0, G=iter1. トリミングあり。

<slit_i2j2.jpg> (i2, j2) plain, scale=(-0.17,0.17), iter<17787, R=iter0, G=iter1.

<slit_ii2jj2.jpg> (i,i2)+(j,j2) plains overlap, scale=(-0.17,0.17), iter<17787, R=iter0, G=iter1.
T20: 16元数(Sedenion)も8元数ライブラリにかぶせてコーディングします。
デバックは4,8元数の結果を16元数の後半の虚部を0として行います。零因子{E(3)+E(10)}*{E(6)-E(15)}で行います。
例 {r,r,r,1; r,r,r,r; r,r,1,r; r,r,r,r}*{0,0,0,0; 0,0,1,0; 0,0,0,0; 0,0,0,-1}=0
rは[-1,1]区間の一様乱数値です。
SedenionのiterationはOctonionと同じです。
Iteration 0: S(n+1)=S(n)**2+S(n)+A*S(n)+S(n)*B+A*B, S(0)=(....),
Iteration 1: S'(n+1)=S'(n)**2+S'(n)+S'(n)*A+B*S'(n)+B*A, S'(0)=(....).
何故、2次形式だけなのかと聞きたいですか?Octonion以上は乗算の結合則が成立しないため 0={(S+A)(S+B)}(S+C)+(S+A){(S+B)(S+C)}とする必要がある。さらにA,B,Cの交換対称性まで導入する必要がある。それで2次までで止めています。
次にS(0),S'(0)の決定ですが、16元数だから零因子A,Bの近傍にとります。
A=(0,0,0,1; 0,0,0,0; 0,0,1,0; 0,0,0,0),
B=(0,0,0,0; 0,0,1,0; 0,0,0,0; 0,0,0,-1).
このママでは{S(i)}が即、発散してしまうので、スカラー定数0.01を乗じて、
さらにA,Bの0,1要素を反転した~A,~Bを使って、スカラー定数δを乗じて、
S(0)=-0.01*A+δ*(~A),
S'(0)=-0.01*B+δ*(~B).
iterationの初期値を同値としたいので、
S(0)=S'(0)=-0.01*(A+B)+δ*{~(A+B)}, δ=0.001.
とする。Scale=[-0.015,+0.015], iter < 500k.

<S3.png> iteration0, R(x,y)=(k4,k) plain, G=(k4,j2), B=(k4,j3).
Rのtraceを見るとk4=0,k=-0.01に収束しているのでA点。
G: k4=0, j2=0, then A-point.
B: k4=0, j3=-0.01, then A-point.
3軌跡とも零因子Aに収束。

<S4.png> iteration 1: R(x,y)=(k4,k) plain, G=(k4,j2), B=(k4,j3).
R: k4=0, k=0, ?A,Bでない点に収束。
G: k4=0.01, j2=-0.01, then B pint.
B: k4=0, j3=0.01, ? 別の零因子点か

<S5.png> iteration0/1 overlap, R=(k,j2), G=(j3,k4), B=(k,j3),
R: k=0/0, j2=0/-0.01, then ?unknown/B,
G: j3=-0.01/0, k4=0/0.01, then A/B,
B: k=-0.01/0, j3=-0.01/0, then A/B.
以上12 tracesのうち9がA,B点に収束している。
16次元の空間の中に0ではないが、積を取ると0になる点が散在している。
そのため、その近傍では2次itrationのtraceが吸引される。
T21: Iterationについて、もう少し調べます。
2次の複素方程式 0=(Z+A)(Z+B)=Z**2+(A+B)*Z+A*B
をZ≠0で除算して 0=Z+(A+B)+A*B/Z, この式から、
Z=2*Z+(A+B)+A*B/Z,
Z(n+1)=2*Z(n)+(A+B)+A*B/Z(n),
というitererationを導出する。
Z(0)=-A or -B で計算すると、どうなるでしょうか?
S11: Z(0)≠1/Z(0); |Z(0)-1/Z(0)|≠0だから、そもそもiterationにならないので、発散する。
T22: 誤差なし計算なら Z(n+1)=Z(n)=-A or -B で Z(n)+(A+B)+A*B/Z(n)=0
だから不動点になる。コンピュータでは誤差なし計算はできないから
Z(n)+(A+B)+A*B/Z(n)=δとなって発散する。収束半径が~0。
それで収束半径を拡大したい。
1/w=1/w +Z(n)+(A+B)+A*B/Z(n), Z(n+1)=1/w, とする。
iterationは1/w=1/Z(n) +Z(n)+(A+B)+A*B/Z(n), Z(n+1)=1/w.
実際にコーディングして計算しましょう。
A=(0.01,0.01), B=(-0.01,0.01), Z(0)=(-0.1,-0.2), iter<20k.

<divideIter.png> scale=[-0,2,+0.2], (Re,Im)-plain
divide iter=今回のiteration, normal=従来の2次形式iteration
両軌跡とも根-Aに収束しています。
Normal/Divide iterationの収束半径図です。scale=[-2,+2], iter<2k,


<NormRadi.png> <DivRadi.png>
ともに白い所が収束する領域です。
T23: 初期値集合{Z(0}が描く画像を調べます。
集合は{Z(0)+uniform random numbers*}
*complex(rand0, rand1), -scl < rand0/1 < +scl, scl=parameter(>0)
です。要素数は10~50kとします。mod(iteration#,4)の値で点描に色をつけます。{赤、緑、青、灰}とします。
A=(0.01,0.01), B=(-0.01,0.01), Z(0)=(-0.1,-0.2), iter<20k.

<normIter40k.jpg> scale=[-0.3,0.3], biasXY=(0.1,0), scl=0.3, element#=40k,
Z(0)=(-0.01,-0.01), iter<20k.
これが Z(n+1)=Z(n)**2+(A+B+1)*Z(n)+A*Bの集合軌跡です。モアレもあります。
1/w=1/Z(n) +Z(n)+(A+B)+A*B/Z(n), Z(n+1)=1/wの軌跡は収束半径で分かりますが、まったく異なります。Z(0)=(1.687,1.650), iter<20k.

<divIterX4.png> scale=[-3,+3], biasXY=(1, 1), scl=1, element#=10k.
Z(0)の値は収束半径図で黒い部分です。Z(0)集合が緑色の正方形として見えています。それが変形されて原点Oに収束しています。
収束が急速なので正方形の辺が見えます。normal iterationでは辺は見えません。
T24: Iteration: 1/w=1/Z(n) +Z(n)+(A+B)+A*B/Z(n), Z(n+1)=1/w,
はZ**-1から導出しました。Z**-0.5, Z**-0.25からですと、
w**0.5=Z(n)**0.5 +Z(n)**1.5+(A+B)*Z(n)**0.5+A*B*Z(n)**-0.5, Z(n+1)=w**2;
w**0.25=Z(n)**0.25 +Z(n)**1.75+(A+B)*Z(n)**0.75+A*B*Z(n)**-0.25, Z(n+1)=w**4.
A=(0.01,0.01), B=(-0.01,0.01), Z(0)=(0,0), iter<20k.
の収束半径図を計算します。
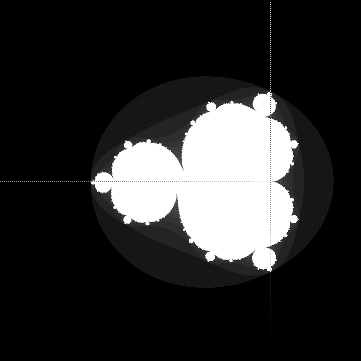

<Iter05.png> <Iter025.png> scale=[-2,+2], biasXY=(1,0) です。収束の境界はフラクタルです。Z**-0.5は2種類存在しますが、どちらでも同じ結果を得ます。
T25: シフトレジスタを使うiterationについて議論します。
Z(n+2)=Z(n+1)**2+(A+B+1)*Z(n)+A*B, でした。
根-A,-Bに収束させるためなら、
Z(n+2)=Z(n+1)+ Z(n+1)**2+(A+B)*Z(n)+A*B, とする方が収束半径が広いでしょう。
類似iterationが多くなったので式に標識を付けます。
norma0l: Z(n+2)=Z(n+1)**2+(A+B+1)*Z(n)+A*B,
type 0A: Z(n+2)=Z(n+1)+ Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0B: Z(n+2)=Z(n)**2+(A+B+1)*Z(n+1)+A*B,
type 0C: Z(n+2)=Z(n)+ Z(n)**2+(A+B)*Z(n+1)+A*B,
type 0D: Z(n+2)={Z(n+1)+Z(n)}/2 + Z(n+1)**2+(A+B)*Z(n)+A*B,
...
以上無限個のiterationが考えられます。
これらの式を見て、現在を計算するためのsuffix(添字) "n"と次世代を定義する、第2のsuffixを分離して"m"とした方が便利でしょう。
Z(m+1)=g{Z(m)}+f{Z(n)}; n=0,1,2,..., m=0,1,2...
今までの議論はm=0だけのiterationです。nも0,1。
このn,m-suffixesを使う式も現在→次世代という1:1のoperationだけです。
これを拡張しましょう。
S12: 2種類の現在系が2世代を生成する2:2システムの例:
Z(m+1)=g{Z(m)}+f{Z(n)},
Y(m'+1)=p{Y(m')}+q{Z(n')}, として世代生成関数を混合する。
Z(m+1)=gp{Z(m),Y(m')}+f{Z(n)},
Y(m'+1)=pg{Y(m'),Z(m)}+q{Z(n')}, gp()≠pg().
なんだか夫婦と2人の子供の世界ですね。しかも4人の別個の発展=iteration(時間的なもの)が存在する。
T26: 多様性を生み出す「最も簡単なシステム」として考えられる系です。
ただしZ(m+1)を次の計算ではZ(m)として使うので、生命体とは違う。
具体的な関数形を定義して計算して見ましょう。
norma0l: Z(n+2)=Z(n+1)**2+(A+B+1)*Z(n)+A*B,
type 0B: Y(n+2)=Y(n)**2+Y(n)+(A+B)*Y(n+1)+A*B,
A=(0.01,0.01), B=(0.01,-0.01),
Z(0)=(-0.01,-0.01),Z(1)=conj{Z(0)}, Y(0)=-Z(0),Y(1)=conj{Y(0)}.
とします。Z(i),Y(i)は独立です。初期値に対称性を入れます。デバックのためです。
結果: iteration=2552=Nで、Z(N)=(-1.915,0.8468), Y(N)=(-0.01,-0.01)です。
{Y(i)}は根Aに停留しました。{Z(i)}は発散です。
norma0lc: Z(n+2)=(Z(n)+Y(n))/2 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bc: Y(n+2)=(Z(n)+Y(n))/2 +Y(n)**2+(A+B)*Y(n+1)+A*B,
として、半分混合します。
結果: iteration=2600=Nで、Z(N)=(-0.01003,-0.009989),
Y(N)=(-0.01003,-0.009987)です。
{Z(i)}{Y(i)}ともに根Aに接近しました。
10倍離れた初期点、Z(0)=(-0.1,-0.1),Z(1)=conj{Z(0)}, Y(0)=-Z(0),Y(1)=conj{Y(0)}.
でもiteration=20kでZ(20k)=(-0.01,-0.01),Y(20k)=(-0.01,-0.01)
と停留点に達します。{Z(i)}の軌跡図。

<ZiTrace.png> scale=[-0.02,+0.02] トリミング
収束半径ギリギリの点、
Z(0)=(-0.349,-0.349),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)}.
iteration=20kでZ(20k)=(-0.0236,-0.0103),Y(20k)=(-0.0236,-0.0102)
です。{Z(i)}の軌跡図。

<Zi2trace.png> scale=[-0.05,+0.05], biasY=-0.03.
{Y(i)}の軌跡も同様です。螺旋を描いて停留点に接近しています。
両者の独立性を高めます。
norma0ld: Z(n+2)=(Z(n)+Y(n)/4)/1.25 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bd: Y(n+2)=(Z(n)/4+Y(n))/1.25 +Y(n)**2+(A+B)*Y(n+1)+A*B,
Z(0)=(-0.1,-0.1),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)}.
iteration=20kでZ(20k)=(-0.01,-0.01),Y(20k)=(-0.01,-0.01) :根A
です。{Z(i)},(Y(i)}の軌跡図。
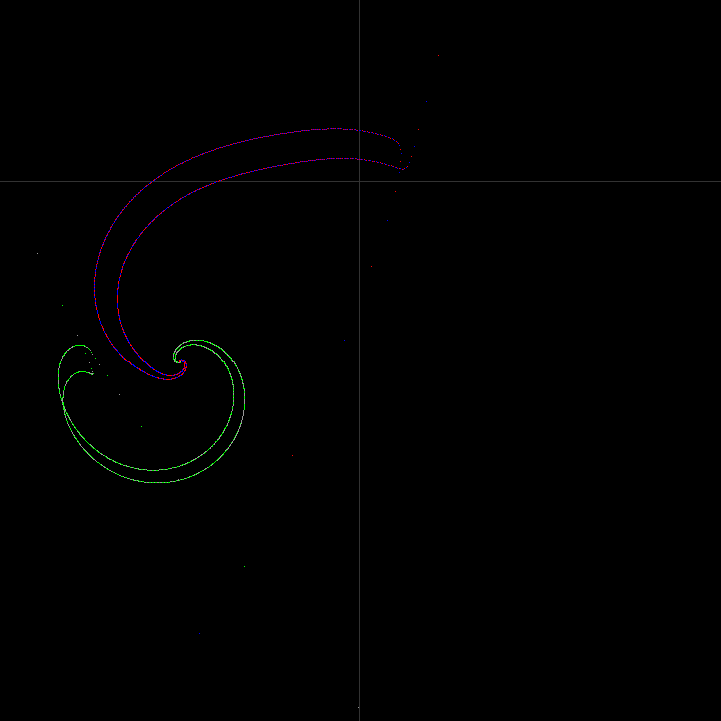
<ZY_trace.png> scale=[-0.02,+0.02], biasY=0.01
両者の軌跡は形状は似ていますが、明確に区別できます。
Z(0)=(-0.2,-0.016),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)}.
Z(200k)=(-0.02238,-0.00999),Y(200k)=(-0.02238,-0.00999)
根ではない(!)停留点です。{Z(i)},(Y(i)}の軌跡図。

<ZY2trace.png> scale=[-0.05,+0.05], biasX/Y=0.02/-0.02
T27:
norma0ld: Z(n+2)=(Z(n)+Y(n)/4)/1.25 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bd: Y(n+2)=(Z(n)/4+Y(n))/1.25 +Y(n)**2+(A+B)*Y(n+1)+A*B,
Z(0)=(-0.2,-0.016),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)}.
Z(0)を中心として実・虚部±1.5の範囲のの収束半径を求めます。
iter<2k, |Z(i)| or |Y(i)| > 2.となった時のLn(iter#)を[0,255]の輝度域にスケーリングした図です。

<ZY_Radi.png> scale=(-1.5,1.5), O=Z(0)
収束域が1つの閉領域ではありません。複数の(おそらく無限個の)停留点が存在し、(!)根ではありません。
norma0ld: Z(n+2)=(Z(n)+Y(n)/2)/1.5 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bd: Y(n+2)=(Z(n)/2+Y(n))/1.5 +Y(n)**2+(A+B)*Y(n+1)+A*B,
Z(0)=(-0.1,-0.1),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)}.
Z(0)を中心として実・虚部±1.5の範囲のの収束半径を求めます。
iter<2k, |Z(i)| or |Y(i)| > 2.となった時のLn(iter#)を[0,255]の輝度域にスケーリングした図です。

<ZY2Radi.png> scale=(-1.5,1.5), O=Z(0)

<ZY2RadiUp.png> scale=(-0.55,0.55), biasX/Y=-0.85/-0.85, O=Z(0)
発散領域(黒~灰色部)と収束部(白)が複雑に入り混じり、興味深いです。
T28: 2 iterations の相互作用式、
norma0ld: Z(n+2)=(Z(n)+Y(n)/4)/1.25 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bd: Y(n+2)=(Z(n)/4+Y(n))/1.25 +Y(n)**2+(A+B)*Y(n+1)+A*B,
Z(0)=(-0.2757,-0.2755),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)},
の周辺の初期値集合について調べます。
集合を、
{Z(0)+cmplx(rand0,rand1)*Sr},{Y(0)+cmplx(rand2,rand3)*Sr}, 0<Sr<1.
とします。ここで -1<rand0<1 一様乱数、rand1~3も同じ。defalt Sc=max{scale value}. 対称性Y(0)=Z(0)を入れます。結果:

<ZYasm35.png> scale=[-0.35,+0.35], biasX/Y=0/0, iter<2k, Nrand<100.
矩形集合が停留点に収斂しています。原点近傍の拡大図。

<ZYasm05.png> scale=[-0.05,+0.05], biasX/Y=0/0, iter<2k, Nrand<100.
集合要素数を10倍にします。Nrand=1k,
iter<2kで|Z(i)| and |Y(i)|が2以上に成らない、発散しない要素数は40.9%でした。
全軌跡を描くと収拾がつかないので、最後1900~2000 iterだけを描きます。
集積点座標:
1象限 Z= (0.0233, 0.0150), Y= (0.0229, 0.0159) not root B=(0.01,-0.01)
2 Z=(-0.0264, 0.0131), Y=(-0.0260, 0.0121) not root B
3 Z=(-0.0100,-0.00998), Y=(-0.0100,-0.00999) ~ root A=(-0.01,-0.01)
第1,2象限の集積点は根ではない。
第3象限のものは根Aである。軌跡の動きが根と集積点では異なる。

<ZYasm05Last100.jpg> scale=[-0.05,+0.05], biasX/Y=0/0, iter<2k, Nrand<1k.
停留点近傍で再び集合が復活しています。違いは:元の形状は正方形ですが、直線状になっています。
S13: 「停留点近傍で再び集合が復活」はエントロピー増大則に反するのでは?
T29: iterationは現世界とは違い、物理法則が無いからなあ。気にする必要は無いと思うが。それに根に停留するような条件が暗に入っている。
或る状態になる確率が定義できれば、確率から情報エントロピーが計算できるか。いや確率をみるよりも、1点{Z(0)}を中心とした半径rの円内に均一に点を分散させ、円内の点の分布を動径histogramで、点の単位面積あたりのdensity変化を追ってみますか。
r=0.01として円内部に均一に分布する点を7525個置き、これを
norma0ld: Z(n+2)=(Z(n)+Y(n)/4)/1.25 +Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0Bd: Y(n+2)=(Z(n)/4+Y(n))/1.25 +Y(n)**2+(A+B)*Y(n+1)+A*B,
Z(0)=(-0.2757,-0.2755),Z(1)=conj{Z(0)},Y(0)=-Z(0),Y(1)=conj{Y(0)},
の周辺の初期値集合について調べます。
集合を、
Z'(0):={Z(0)+uniform distribution points in a circle},{Y(0)=-Z'(0)}.
計算量は7525*iteration# 2k。
Circle's radius=0.01 で histrogramを調べる範囲を0.02とする。
Density=points numbers in [R0,R1], R0<R1, R1-R0=0.001とする。
半径0.02内に0.001違いの同心円を20個作って、その動径方向のdensityを計算する。即、プログラミングしましょう。

<Zasm_trace.png>
これが結果です。縦軸は情報量を意識して対数目盛(常用対数)で、横軸が点集合の重心からの半径。初期値it=2では半径0.01内の均一density、実際そうなっている。
100回iteration(青)すると、分布は平均化する。ここまでは予想通り。
1k回iteration(緑)では、分布が局在化しはじめる。
2k回(赤)では局在化が顕著になる。分布はGaussianのように見える。
一旦散開して再度、別の分布(多分正規分布)に収斂している、と考えられる。これは根位置に収束する、という巡回式から妥当な挙動です。
{Y(i)}の軌跡です。

<Ylast100.png> scale=[-0.05,+0.05] mod(iteration,4)で赤、緑、青、灰の順に色を付けています。mod(2)でほぼ同一位置に来ています、ゆえに紫と灰緑のパターンになっています。形状は{Z(i)}とほとんど同じです。

{Yi)}の重心まわりのradius=0.02円内の角度histogram図です。

<Yasm_angl.png> iteration#と点数も記しました。
角度から見ると、iteration数の増大に依存して局在化しています。
ただし点数は減少し再び増大し(radial方向の収縮による)、その後ゆっくり減少しています。局在化しないtraceは円外へ発散しています。
この巡回式は角度分布で見ると構造を生成しています。
T30: 今までA,B,Cは定数でした。これがiteration=2001で突然、
A'=rot*A, B'=(rot**-1)*B, C'=A'*B', と変化したら軌跡はどうなるのでしょうか?
rot={cos(θ), sin(θ)}, rot**-1={cos(-θ), sin(-θ)}={cos(θ),-sin(θ)},
then; C'=C. (A+B)'=cos(θ)*Re(A+B)+Im(A+B).実軸に沿った変形です。
θ=π/20=4.5[deg], iteration<2100で計算してみました。
全軌跡のプロット数比 0.426(θ=0) -->0.323(θ=π/20)
A,Bの変化によりiteationが発散しています。
Last100の図を見ていただくのが分かりやすいでしょう。

<Zlast100T0.png> θ=0, scale=[-0.05,+0.05]
<Zlast100.png>と同じように見えますが、両者を同じフォルダに入れて交互に見ると、第3象限の根の周辺で軌跡が回転していることが分かります。試してください。

<Zlast100T4.png> θ=π/20. scale=[-0.05,+0.05]
明確に発散に移行しています。iterationを4kまで延長すると新A' or B'点に収斂します。
θ=0, 4.5, 9, 18 [deg]と増大させると、
全軌跡のプロット数比は 0.426, 0.323, 0.239, 0.107 と小さくなります。
last100の軌跡図では第1,2象限の集積点付近は大きな変化はありませんが、
第3象限の根周辺の軌跡数はどんどん小さくなります。根が移動しているので当然です。
T31: 以前、
>>T25: シフトレジスタを使うiterationについて議論します。
Z(n+2)=Z(n+1)**2+(A+B+1)*Z(n)+A*B, でした。
根-A,-Bに収束させるためなら、
Z(n+2)=Z(n+1)+ Z(n+1)**2+(A+B)*Z(n)+A*B, とする方が収束半径が広いでしょう。
類似iterationが多くなったので式に標識を付けます。
norma0l: Z(n+2)=Z(n+1)**2+(A+B+1)*Z(n)+A*B,
type 0A: Z(n+2)=Z(n+1)+ Z(n+1)**2+(A+B)*Z(n)+A*B,
type 0B: Z(n+2)=Z(n)**2+Z(n)+(A+B)*Z(n+1)+A*B,....
という議論をしました。 ここで一般化します。
Z(n+1)=Z(n)+Πp{Z(n)+A(p)}, initial: Z(0).
execution: Z(0),-->Z(1), Z(1)--->Z(2),....
Πの意味は「乗算の連続」です。変形して、
Z(n+2)=Z(n)+Πp{Z(n+1)+A(p)}*Πq{Z(n)+A(q)}, initial: Z(0),Z(1).
Z(n+3)=f{Z(n), Z(n+1), Z(n+2)}
+Πp{Z(n+2)+A(p)}*Πq{Z(n+1)+A(q)}*Πr{Z(n)+A(r)},
initial: Z(0),Z(1),Z(2).
etc.
{A(p)}を中心(0,0)、半径Rの円周上に取ります。
A(0)=(0.1,0)を反時計方向に10deg毎に回転してA(1),A(2)....A(35)とします。
巡回式: Z(n+3)=Z(n)+{Z(n+2)+A(1)}*{Z(n+1)+A(2)}*{Z(n)+A(3)},
Z(0)=(0.01,0.01), Z(1)=Rot(2π/3)*Z(0), Z(2)=Rot(4π/3)*Z(0).
Z(0)を中心として半径0.01の円内に均一に7525個の点を取り、
それらを新たに{Z(0)}とします。その集合のRot(2π/3), Rot(4π/3)操作を{Z(1)},{Z(2)} とし、iter=2kの軌跡のLast100を複素平面に プロットした図です。

<Z4try.jpg> scale=[-0.1,0.1], biasX/Y=-0.1/0.
根は-A(1),-A(2),-A(3)なので-A(1)に収斂しているようにみえますが、Re軸値は-0.08です。
{Z(0)}の初期集合の形状は円です。iter=2k後も形状は保たれています。
根の近くに収束するので、今度は根をA(1),A(10),A(19)と分散させます。
その結果です。Last100部分のみ。
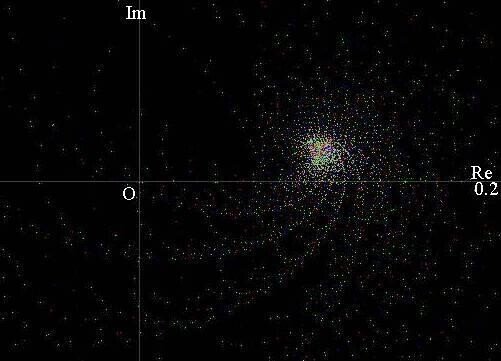
<Z4try2.jpg> scale=[-0.2,0.2], biasX/Y=0/0. トリミング。
全点の2%しか残っていません。第1象限の集積点(0.100,0.019)ほぼ-A(19)です。プロット点が少ないのでLast400で描いてみます。

<Z4try216.png> scale=[-1.7,1.7], biasX/Y=0/0. 軌跡の分散状況に注目。
T32: 根Z={A(0)~A(35)}で空間を囲ったらどうなるのでしょうか?
Z(n+3)=Z(n) +[{Z(n+2)+A(0)}{Z(n+1)+A(1)}{Z(n)+A(2)}]
*[{Z(n+2)+A(3)}{Z(n+1)+A(5)}{Z(n)+A(6)}]
....
*[{Z(n+2)+A(33)}{Z(n+1)+A(34)}{Z(n)+A(35)}],
ここで多項式に一種の対称性を入れています。
初期値 Z(0)=(0.01,0.01), Z(1)=Rot(2π/3)*Z(0), Z(2)=Rot(4π/3)*Z(0).
Z(0)を中心として半径0.01の円内に均一に7525個の点で計算しました。
全て円周状に並べた根の内側の点です。Lat100のプロット。

<Z4try35.png> scale=[-0.35,0.35], biasX/Y=0/0. トリミング。
軌跡は2点間を振動しています。円状初期値の範囲は保たれています。
では円周状に並べた根の外側の点ではどうなるのでしょうか?
Z(0)=(R,R), R→∞ で計算します。
R<0.5では、円状初期値の範囲が保たれています。
R=0.6では、形状が崩れ、長く伸びてきます。
R=0.65では、拡散します。
R=0.67では、再び収斂方向になり、R=0.7では発散に向かい、R>0.71では急速に発散します。
収束半径~0.5です。それより外側では発散する図形になります。
例: R=0.71, iter=2kで55%の点が原点から半径2以内に残っています。
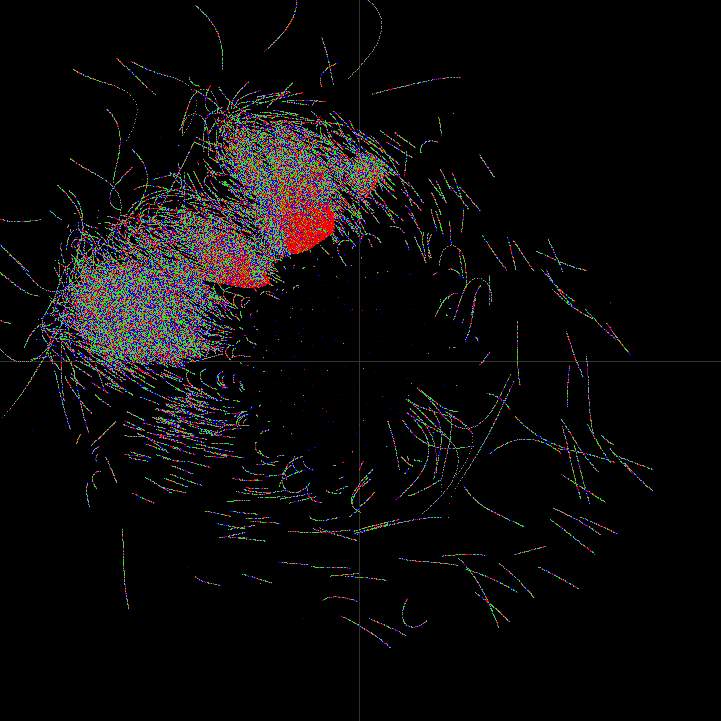
<Z4try3507.png> scale=[-1.3,1.3], biasX/Y=0/0. 発散図形の典型例です。
iter>100をプロットしました。
S14: 3次方程式の発散図は見栄えがします。虚軸上に2根、実軸上に1根、
Z(n+3)=Z(n)+{Z(n+2)+A(9)}*{Z(n+1)+A(18)}*{Z(n)+A(27)},
Z(0)=(0.53,0.0), Z(1)=Rot(2π/3)*Z(0)=Z(2), iter>100, plotting ratio 51%.

<Z4try3_53.png> scale=[-0.5,0.5], biasX/Y=0/-0.4.
T33: 巡回式の軌跡は空間とは作用していません。式の点列はphotonのような素粒子ではありません。
<Z4try3_53.png>のような発散軌跡は粒子の流れを想起させます。
これを利用して軌跡を障壁で妨害します。こうして「流れ」のようなものの性質を調べます。
障壁を B0 < Im{Z(n+3)} < B1; B0/1=real, この領域で軌跡を消滅(stop the iteration)させます。
[B0,B1]=[0.85,1]*, plotting ratio 5.9% 図は下
[B0,B1]=[0.85,1.15]**, plotting ratio 2.9% 図は下
[B0,B1]=[0.8,1.2], plotting ratio 0.7%
[B0,B1]=[0.75,1.25], plotting ratio 0.04% 一本のビームです。

<Z4try3_531.png> scale=[-0.5,0.5], biasX/Y=0/-0.4, blocked area is "*".

<Z4try3_532.png> scale=[-0.5,0.5], biasX/Y=0/-0.4, blocked area is "**".
虚軸に垂直な障壁により軌跡のビームが絞られます。
普通のflowではありません。厚い障壁により数本のビームにまで絞れます。
トンネル効果を予測したのですが違います。
B0 < Re{Z(n+3)} < B1; B0/1=real この領域で軌跡を消滅させます。
[B0,B1]=[-1.2,-0.8], plotting ratio 0.7% ビームが同様に絞られます。
[B0,B1]=[0.333,0.366], plotting ratio 5.0% 分散した弱いビームと強い1本のビームが得られます。色は軌跡のmod(4)で表したphaseです。
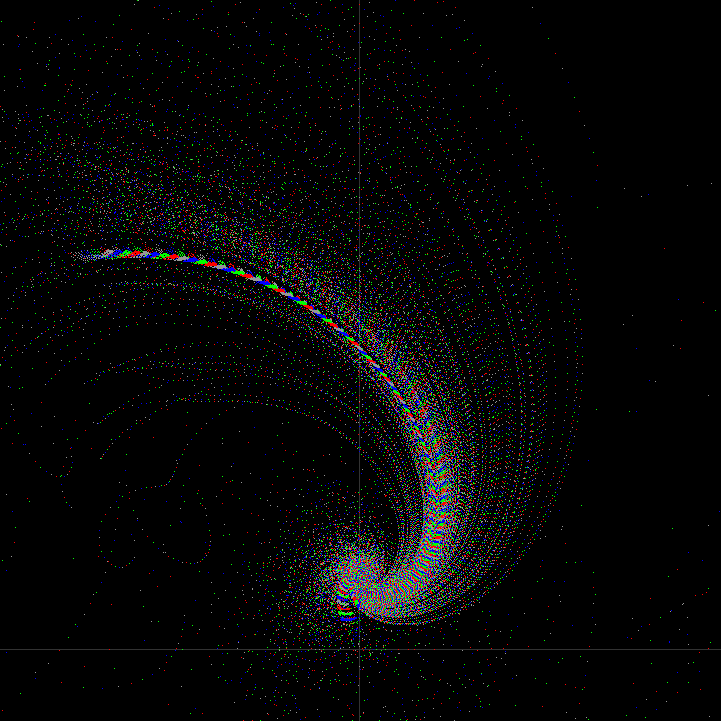
<Z4try3_533.png> scale=[-0.5,0.5], biasX/Y=0/-0.4.
矩形障壁:B0 < Im{Z(n+3)} < B1 & B2 < Re{Z(n+3)} < B3;
[B0,B1]=[0.2,0.3] & [B2,B3]=[0.2,0.3]. これでプログラミングします。

<Z4try3_534.png> scale=[-0.5,0.5], biasX/Y=0/-0.4.plotting ratio 44%
矩形の暗部が見えます。ただし元の位置より斜め右上に動いています。動いた跡も見えます。この現象は興味深いです。iteration点列はphotonではありませんが、影を生じます。矩形を原点近くに移動します。
[B0,B1]=[0.1,0.2] & [B2,B3]=[0.1,0.2].

<Z4try3_535.png> scale=[-0.5,0.5], biasX/Y=0/-0.4.plotting ratio 9%
矩形の影(暗い正方形)から上方へ第2の影が見えます。
T34: 前回は障壁を軌跡を吸収する、停止させる領域としました。
今回はその領域でiterationの根{A(i)}部分を変化させる、とします。
根を変化させると、巡回式の形が変化し、軌跡の進行方向も変わります。
光で言えば屈折です。
領域 [B0,B1]=[0.03,0.07] for Im & [B2,B3]=[-0.1,0.2] for Re, において、
Z(n+3)=Z(n)+{Z(n+2)+A(9)}*{Z(n+1)+A(18)}*{Z(n)+A(27)}, を
Z(n+3)=Z(n)+{Z(n+2)+A(9)}*{Z(n+1)+A(27)}*{Z(n)+A(0)}, に変更する。
ビームを右方向に回転させようとしている。
Z(0)=(0.53,0.0), Z(1)=Rot(2π/3)*Z(0)=Z(2). iter>100 をプロットしました。

<Z5_02.png> scale=[-0.5,0.5], biasX/Y=0/-0.4. plotting ratio 51%
実軸に平行に置いた0.04の薄い矩形領域の屈折作用様のビーム分散が見えます。
T35: Conclusion (9/2, 2021) 今までの試行プログラミングの概要です。
有限要素空間を無質量の点が進行していく、という条件の下で;
その進行を誘因する(1)複素方程式の根、
複素方程式から巡回式に変形するための「点の進行を記述する」方程式の両辺に付加した、
(2)次世代生成項、
(3)巡回式の複素変数をシフトレジスタ的に書き換える方法、を提示しました。
(4)上記の手段により生成される点集合は、巡回式の初期値により識別されます。
(5)その初期値の集合は、無質量の点集合の「有限空間内の」流れ(flow)を識別します。
(6)ここまでは、有限空間は点の進行に関与しません。点の位置の存在だけを保証しています。
空間内に別のサブ空間(領域)を設定し、そこでは方程式そのものが消滅、あるいは根が変化する、
という「空間の性質」を他とは異なるように設定します。
そうして、その「領域」の影や屈折と命名した「空間の性質」がもたらした現象の存在を示しました。
(7)有限要素空間と我々の生存する3次元(時間を含めれば4次元)連続無限空間とは異なるのに、
そして素粒子のような物質とは全く異なる、運動量も定義できない、位置のみの点の集合が、
その動きを規定する、方程式の根集合の空間分布の変化により、
我々の知っている複数の物理現象の一面を示すのは興味深いです。
この記事が気に入ったらサポートをしてみませんか?
