スラロームのユニークネス解説

hyaxn

どうも、ヒャンです。

最近はスラロームの作問にハマっております。スラロームはウネウネ線が伸びまくるのが面白いと個人的には思っているので、大きめの盤面で隙間を縫うようにギュウギュウ詰めに線が通っていく展開が好きです。


最近のはパズスクに載せてるので、昔のやつを宣伝。本記事の主題とは関係ありません。比較的表出旗門番号が多めなので、ユニークネスに頼らなくてもそこそこ解けると思います。

話を戻して、ギュウギュウ詰めに線が伸びていくような問題の多くはユニークネスを利用して解くのが有効です。拙作の大半はユニークネスでゴリゴリ進めてもらうことを想定しています。旗門番号をある程度無視してゴリゴリ線を伸ばしていくので、ナンバーリンクに近い感覚があると思います。

ざっとインターネット上を探した感じ、スラロームのユニークネスパターンについて解説してる記事は見当たらなかったので、自分自身の勉強も兼ねて残しておきます。


注意

スラロームでは、ユニークネスをフル活用すると、解き方がガラッと変わります。そのため、本来の面白さを損なう恐れがあります。

個人的な考えですが、スラロームというパズルは、「番号の表出していない旗門の番号を推測しながら、どう旗門を通していくか、どう繋げていくかを考えて解く」のが本来の姿であると思っています。しかしユニークネスを持ち込めば、問題によっては旗門番号を一切見ずに線を伸ばして繋げて正答することもできてしまいます。このような意味で、本来の面白さを損なうと述べました*1。

（1年前にユニークネスを身に着けたときの姿。）

じゃあ何故わざわざそれを広めるような記事を書くのか。それはユニークネスをフル活用して解いていくのはまた違った面白さがあるからです。また、ユニークネスを敢えて封じるような問題も最近は見受けられます。こうした問題はユニークネスを知っていることで逆に楽しめます。別の視点として、問題を早く解くためのテクニックに貴賤はないという考えもまたあります。


具体例

やや前置きが長くなりました。
「複数解にならないか吟味する」で以降に示すパターンは全てカバーできます。ユニークネスだからまあ当然です。とはいえ、それではこの記事の意味がないので、例えばこんな形がありますよという例を以降に示します。ユニークネスが使える形は本当に無数にあるので、あとはやりながら慣れるしかないです。

注意点ですが、ユニークネスにおいて、スタートとゴールの○は結構複雑な挙動をします。以降のパターンは基本的に○が絡まない想定です。


1. 線の延長

線の繋げ方1非常によく見る形。仮に左下の空間にある2本の線がすぐに繋がるとすると、明らかに複数解です。別の旗門を通った後でなら繋がる可能性はあります。
ちなみにユニークネスを使わない場合、旗門番号から推定することになります。

画像3逆に上図のようにどうしても空間が余っちゃうみたいな場合、問題が唯一解であるならばどこかで解き間違えています。

線の繋げ方2例えば上図の盤面は、赤く印をつけた黒マスを置かないと唯一解になりません。大きく開けた空間に黒マスが浮かんでいる場合、線が綺麗に並ぶ可能性が高いです（勿論100%ではない）。


1_線の延長3線が曲がるポイントでも使えます。上図の場合、線の繋がり方が2パターンあるため、どの線も繋がりません。


画像13

スラロームでは、90°に曲がった線の進み方は上図の左側のような制約を受けます。これは、線の伸び方に絶対的な禁止系があることに由来します（上図の真ん中及び右）。

画像14

そのため、線が90°曲がるときには上図の3パターンの何れかになります。左側のパターンの場合、新たに生えた左下の90°部分が同様の制約を受けます。従って、斜めに並んだ90°部分は、最後に黒マスまたは旗門にぶつかります。実戦では内側を塞ぐものがないのに線を曲げないが使いどころかと思います。


画像6

唐突ですが演習問題1-1です（上図）。唯一解であることが保証されている問題の一部であると考えてください。ユニークネスを駆使してどこまで決まるでしょうか（答えは記事の最後）。ぱずりんく


画像17

演習問題1-2です（上図）。少し配置が変わりました。こちらだとどうなるでしょうか（答えは記事の最後）。ぱずりんく

演習問題1-3です。旗門番号カウント禁止です。ユニークネスだけで線を伸ばして繋げれば正解できるように作ってあります。
（黒マスまみれなのはご容赦ください）


2. 空間への線の侵入

ユニークネスでは、多くの場合空間を埋め尽くすように線が伸びます。そうしないと無駄にぐねぐね曲がって線が伸びることが許されてしまって複数解になるからです。

2_空間への線の侵入1上図の場合、最初に居る線だけでは、赤く囲った空間を持て余します。よって、線が侵入してくる必要があります。ぱずりんくを置いておくので、色々線を引いてみてください。複数解にならない伸ばし方はこれしかないはずです。


画像8

演習問題2-1です（上図）。唯一解盤面の一部にこの形があると仮定して可能な限り線を伸ばしてください（答えは最後）。ぱずりんく

演習問題2-2です。旗門番号カウント禁止。線がグネグネ可能な配置を作らないようにしましょう。

演習問題2-3です。旗門番号カウント禁止。


3. 長い旗門のパターン

さてここまで幾つか挙げてきましたが、何れも旗門が全く関係ないことにお気づきでしょうか。なんにもないとこに線は生やせないため長さ1の旗門は使っていますが、あくまで線を生やすためだけに使っているに過ぎません。
冒頭で述べたとおり、ユニークネスは旗門と直接関係ないところでこれだけ線が引けてしまう強力なツールです。

以降は旗門が絡んだユニークネスのパターンです。

画像9非常に強力なユニークネスです。辺に一番近い端っこを通ります。加えて、画像で言えば左右のどちらかまたは両方に90°に折れ曲がる形で線が入り込みます。

画像10

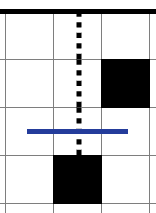
但し長さ3の場合、真ん中が黒マスで塞がれると上図のパターンも有り得ますので注意。

画像12

長さ4以上になると、線の伸び方によっては辺に一番近い端っこを通らないことも大いに有り得ます（上図は一例）。長さ2は確定、長さ3は真ん中が塞がれてなければ確定と覚えると良いかもしれません。

ここで、何故端っこを通るのが確定するかを考えてみます。言葉の選び方が難しいのですが、「その線が端っこを通らないことによって生まれる空間に使い道がないから」です（下図）。

画像19

言い換えれば、「無駄に空間を消費するのはNG」でしょうか（下図はやりがちな禁止系）

画像24

長い旗門の通り方に関するイメージとして、「空間を無駄遣いしない」がセオリーになります。


辺に垂直に立った旗門以外でも、この考え方は活用できます。

画像15

辺にこのような形で置かれた旗門は、端っこを通るか真ん中を通るかの2択があります（当たり前）。このとき、端っこや真ん中を通らざるを得ないように、必ず他の線が伸びてきます。

画像18

空中の場合、上下のそれぞれから左右が塞がれ、真ん中を通らされるようになることもあり得ます（上図）。



画像21

演習問題3-1です（上図）。小ループ禁が無くても答えは変わらないのですが、ヒントとして入れてあります。ぱずりんく

画像23

演習問題3-2です（上図）。結構難しいかもしれません。ぱずりんく


結び

いかがでしたか？（クソまとめサイト）
ユニークネスよくわからんって方の理解の一助になれば幸いです。「複数解にならないか吟味する」「その線の引き方は空間を無駄遣いしてないか？」といった点に注意するとユニークネスが上達するのではないかと思います。演習問題の答えをこの先に記してます。答えが間違ってると思われる方はご連絡ください。実はあまり自信が持ちきれていません…
問題の唯一解性はソルバーで確認してるので大丈夫だと思います。

良きユニークネスゴリゴリスラロームライフを。


演習問題の答え

1-1

画像6

左下の隙間は確実に2通りの通り方が発生するので何があっても通りません。真ん中には空間が発生します。上の旗門2つを通っている線のどちらかを下に伸ばして繋げようとすると確実に複数解です。空間を必ず全て埋め尽くすとは限らない点に気をつけましょう。


1-2

画像17

1-1より決まる部分が少ないです。緑の線は繋がることができません。紫とオレンジが繋がるかどうかは旗門番号等の新たな制約がかからないと決められません。


2-1

画像11


3-1

画像20

平行に並んだ長い旗門は連鎖的に決まっていくことが結構あります。また、1マス空けて辺に平行に置かれた旗門はユニークネス上の制約が強いので決まりやすいと個人的には思っています。


3-2

画像22

実際に解くときは左上のバツ印と線までは引く必要はないと思います。


註釈

*1 さらに一般化すれば、ユニークネスも手筋の一つに含めることもできます。以降は個人的な考えになりますが、手筋集なるものは、言ってしまえばパズルのネタバレです。ゲームで言えば攻略本です。そのため、考え方次第では、そもそも手筋集自体がパズルの魅力を損なうとも言えるでしょう。しかし、ユニークネスには一般の手筋と異なる点があります。それは「唯一解である」という「暗黙の了解」から導かれるものであるという点です。一般の手筋は「明示的に」与えられた「ルール文」から導かれる定理です。ここで、ルール文はパズルを面白くするために練り上げられています。唯一解性は練り上げられたものでもなければ、それがパズルの面白さを産むことは極稀です。ルール文をもとに練り上げられたパズルの空間に対して無機質な唯一解性を持ち込むことは、その空間を破壊することに他なりません。以上の理由により、ユニークネスは取り扱いには注意が必要であると個人的には思っています。




この記事が気に入ったらサポートをしてみませんか？