競プロ精進記録

自分用?に、Atcoderなどで学んだことを書いていきたいと思います。
まだまだ実力不足なので誤りがあるかもしれません。
今日解いたのはこれです。

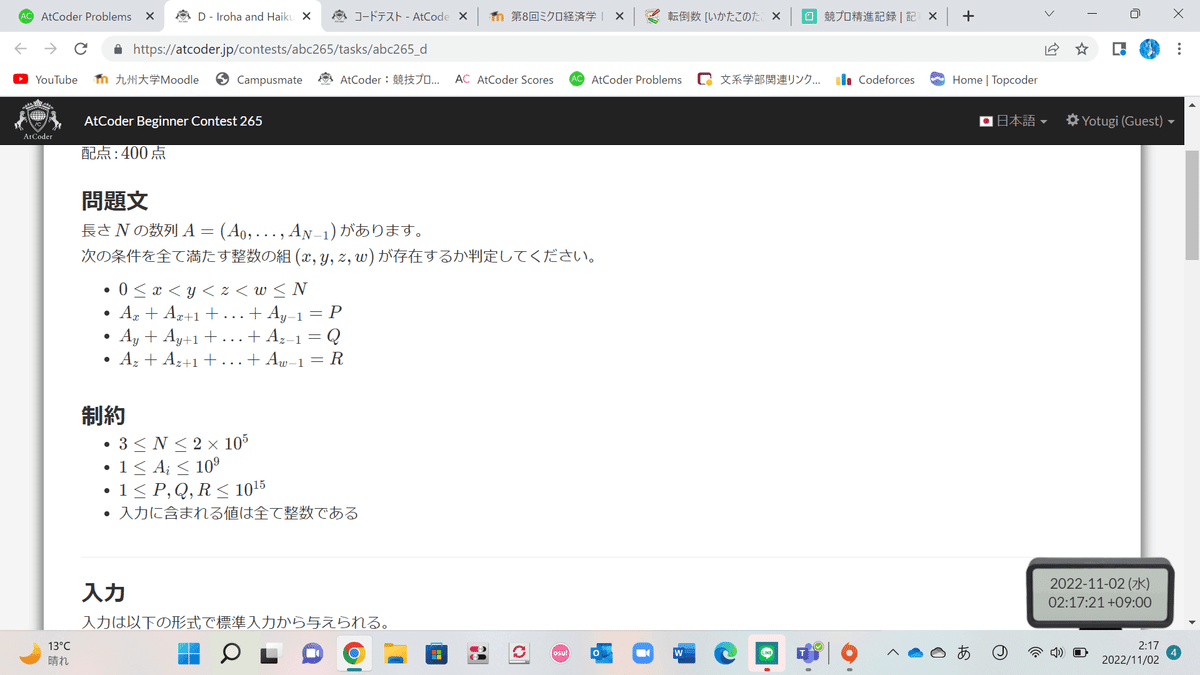
考えたこと

とりあえず制約を見た感じ、O(NlogN)くらいまでなら間に合いそう。
和を求めるには累積和が使えそう。
以上（えぇ…)

いざ実装

とりあえず累積和を使いたいので、下準備として計算しておきます。
a[i]で、a_1+a_2+・・・+a_(i-1)　までの和（ただしa[1] = 0)
とすれば 、P = a[y] - a[x]　みたいな感じでできますね!!
xを決める→ｙを探す→ｙが決まったらｚを探す・・・みたいなノリでコードを書きました。以下が最初に書いたごみコードです。

NlogNとは()

結果

間に合うはずないですね…普通にTLEしました。

どうすればいいのか

まず、何がダメなのか考えてみます。y,z,wを探すとき、for文を用いて線形探索をしてしまっているのがだめですね。線形探索はO(N)の計算量が必要となります。ｘが決まれば x < y　である事を利用して探索範囲を工夫（？）することで、全体の計算量をO(N^2)まで抑えることができますが、普通に間に合いません。しかし、a[i]が単調増加である事に気づけば、二分探索が可能なことが分かります。二分探索はO(logN)なので、全体としての計算量がNlogNですみますね!!これなら間に合いそう！
以下がコードです。

Submission #36134568 - AtCoder Beginner Contest 265

実装がめんどかったです。(二分探索をよく理解していない）
ただなんとかAC出来てよかったです。

まとめ

二分探索をしっかり理解することが大切だと思いました。これからも頑張りたいです。