[学習記録]グラフ理論3
参考資料
https://ocw.hokudai.ac.jp/wp-content/uploads/2016/01/GraphTheory-2007-Note-all.pdf
様々なグラフ
空グラフ ( null graph )
辺集合が無い(空の)グラフ
Nn で表される
完全グラフ (complete graph)
相異なる点がすべて隣接しているグラフ。(ループや多重辺を含まない)
Kn で表される。
辺の数は n C 2 = n(n-1) / 2 で表される
正則グラフ (regular graph)
全ての点の次数が等しいグラフ
Nn:0-正則グラフ
Cn(後述):2-正則グラフ
Kn:n-正則グラフ
閉路グラフ (cycle graph)
次数2の正則連結グラフ
Cn で表される
道グラフ (path graph)
閉路グラフから1つの辺を除いて得られるグラフ
Pn で表される
車輪(wheel graph)
閉路グラフに点を1つ加え、加えた点とその他の点を辺(スポークと呼ばれる)で結んだもの
Wnであらわされる
ピータースン・グラフ
次数列 {3, 3, 3, ,3 , 3, 3, 3, 3, 3, 3, } で表されるグラフ
正五角形の内側に五芒星があるような配置にするときれい
二部グラフ (bipartite graph )
Gの点集合2つの素な集合A,Bに分割し、Gのすべての点はAとBの点を結ぶようにできたとき、Gは二部グラフであるという
完全二部グラフ( complete bipartite graph)
二部グラフのうち、すべての点が異なるグループの点と隣接している場合
k-立方体
ai = 0 or 1 であるベクトル (a1, a2, … ak )に1つの点を対応汗、
一つだけ異なる点に対応する2つの点が辺で結ばれるような正則二部グラフ
Qk で表される
Qk は 2k 個の点と, k2k−1 本の辺を持つ
補グラフ
単純グラフ(G)の補グラフ(Gバー)は、Gが隣接していない点の時、Gバーが隣接するようなグラフ。
・G + Gバー = 完全グラフ
・完全グラフの補グラフは空グラフ(逆は言えない)
・完全二部グラフとその補グラフの和は、完全グラフになる
グラフにまつわるパズル
8つの円の配置問題
図 3.46 のような 8 つの円の中に A,B, C, D, E, F,G, H の 8 つの文字を入れることを考える. ただし, アル ファベット順で隣にくる文字は互いに隣接しないように置く. このとき, このとき, 適切な配置の仕方を答 えよ
隣接しているアルファベットがすくないA, Hを次数が最も多い#1、2におく
#1に隣接していないものは#8のみのため、Bの位置が#8に確定する(Gも同様に)
のこりC,D,E,Fの内、C,Dは隣り合わないようにかつ、D,Eが隣合わないように配置するとC:#3、D:#5,E:#4,F:#6
4つの立方体パズル
対面を辺として表すことで、表面にでる4面を選ぶことができる
H1、H2を見つけるときに、各Cubeの辺を1本ずつ含み、共通な辺が無く、次数2の正則グラフを選ぶ。
H1, H2:前後、左右の面に対応
各Cubeの辺を1本ずつ:たて4つの面(+裏)を4色にする
共通な辺がない:前後、左右で同じ面を使わない
次数2の正則グラフ:4色つかう
選んだH1,H2から積み上げを考える
例題
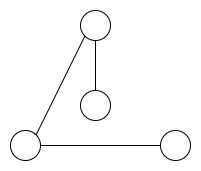
3.1.1 グラフ G の接続行列を求めよ.
M = [
1 1 0 0
1 1 1 1
0 0 1 0
0 0 0 1
]3.1.2 接続行列の各列の要素の和は何を意味しているか ?
辺に接続している点の数
3.1.3 接続行列の各行の要素の和は何を意味しているか ?
点に接続している辺の数
3.1.4 ) e(G) をグラフ G の辺数とすると v∈V (G) Σdeg(v)=2e(G) が成り立つことを示せ
グラフより、e(G) = 4,
deg(1) = 2, deg(2) = 4, deg(3) = 1, deg(4) = 1, Σdeg(v) = 8 = 2e(G)
3.2
完全グラフ K5 について以下の問いに答えよ
3.2.1 図 2.14 の完全グラフ K5 の 5 つの頂点に, 時計回りに番号 1, ··· , 5 を割り当てる. このとき, この 完全グラフの隣接行列 A を求めよ.
A = [
0 1 1 1 1
1 0 1 1 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 0
]
3.2.2 点 1 と点 3 を結ぶ長さ 2 の歩道の数は, A2 の第 (1, 3)-成分に等しいことを示せ.
A2 = [
4 3 3 3 3
3 4 3 3 3
3 3 4 3 3
3 3 3 4 3
3 3 3 3 4
]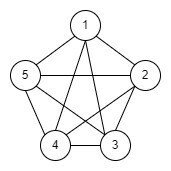
図より、1-2-3, 1-4-3, 1-5-3 = 3個
3.2.3 点 1 と点 3 を結ぶ長さ 3 の歩道の数は, A3 の第 (1, 3)-成分に等しいことを示せ
A3 = [
12 13 13 13 13
13 12 13 13 13
13 13 12 13 13
13 13 13 12 13
13 13 13 13 12
]1-2-1-3, 1-2-4-3, 1-2-5-3,
1-3-1-3, 1-3-2-3, 1-3-4-3, 1-3-5-3,
1-4-1-3, 1-4-2-3, 1-4-5-3,
1-5-1-3, 1-5-2-3, 1-5-4-3,
=> 13 通り = A3(1,3)
3.3 完全三部グラフ Kr,s,t はそれぞれに属する点の個数が r, s, t である 3 つの点集合からなり, 異なる 集合に属する点は全て辺で結ばれているグラフである. このとき, 以下の問いに答えよ.
3.3.1 ) K2,2,2 及び K3,3,2 を描け
K3, 3, 2は省略
3.3.2 Kr,s,t には全部で何本の辺があるか答えよ.
mr = r(s + t) = 15, ms = s(r + t) = 15, ,t = t(r + s) = 12,
m = 42
3.4.1 次の (i)~(v) のグラフがある場合にはそれを 1 つ挙げて描け (無い場合には「無し」と書く).
(i) 次数 5 の正則グラフであるような二部グラフ.
存在する(左端の点に接続している辺以外省略)
(ii) 二部グラフであるプラトン・グラフ.
プラトングラフってなに?
(iii) 車輪である完全グラフ.
存在する
(iv) 11 個の点をもつ 3 次グラフ.
3次グラフ=次数がすべて3のグラフのこと?
=> グラフの変数 m は点数をn とすると m = 3n / 2 となる。mは整数で なければならないため、n=11のものは存在しない
(v) 次数 4 の正則グラフで K5, K4,4, Q4 以外のグラフ
存在する
3.4.2 それ自身の捕グラフと同形な単純グラフは自己捕対 (self-complementrary) であるという. このとき (1) 4 個, または 5 個の点をもつ自己捕対グラフを全て描け
5個、8個は略
3.5 3.58 のような展開図を持つ 4 つの立方体の問題には解が無いことを示せ
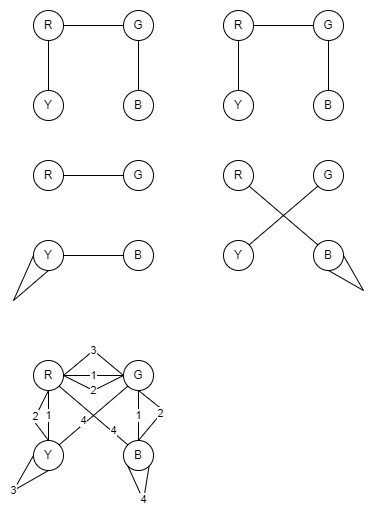
重ね合わせた図から、RB、GYがすべて4からの辺となっているので、グラフを2つ選ぶことができない => 解が無い
3.6.1, 3.6.2
3.6.3
各辺に点を打つ(v1, v2, …vm) 。
もともとある頂点を基準に、ある辺に隣接する辺数は k -1となり、
各点v を結ぶことのできる点の数は 2(k -1)となる。
すべてのvについて同様なので、できた線グラフは正則であり、
次数は2k -2となる
3.6.4
正則グラフの場合のみ?
次数kのL(G)は、3.6.3より、2(k -1)の次数のグラフとなる。・・・①
補悪問題より、 m = n * k / 2 ・・・②
②に①をあてはめ、
m = n * 2(k -1) / 2 = n (k -1)
3.6.5
略
3.7~
いつかやる
この記事が気に入ったらサポートをしてみませんか?
