[学習記録]グラフ理論2

Hota T

2023年3月6日 13:28

参考資料

https://ocw.hokudai.ac.jp/wp-content/uploads/2016/01/GraphTheory-2007-Note-all.pdf

定義と例

単純グラフ

単純グラフ・・・グラフにループが含まれず、頂点のどの対も高々１つのリンクで結ばれているグラフ
V(G)：グラフＧの点集合 vertex set
E(G)：グラフＧの辺集合 edge set
ψg ：グラフＧの接続関数

接続関数とは、Ｇの各辺にＧの頂点を対応させる関数である。
V(G) = { a, b, c } , E(G) = e1, e2, }　のとき、ψg(e1) = ab, Ψg(e2) = bc　となる
a - b - c
e1 e2

同形 ( isomorphic )

２つのグラフG1、G2の間に１対１の対応関係があり、G1の任意の２点を結ぶ辺数がG2の対応する点を結ぶ辺数に等しいとき、G1とG2は同形であるという。

接続関数を用いると、G1, G2が同形であるとき、１対１写像
　　Θ：V(G1)　-> V(G2)
　　Φ：E(G1) -> E(G2)
が、次の関係が成り立つ。
　　ψG1(e) = uv ⇔　ψG2（Φ(e)) = Θ(u)Θ(v)

Θ(u) = l, Θ(x) = p, Φ(ux) = lp　= Θ(u)Θ(x),
ψG1(ux) = ux　⇔　ψG2(Φ(ux)) = ψG2(lp) = lp = Θ(u)Θ(x),
よって、同形であることが確認できる

ラベル付きグラフとラベル無しグラフ

各店に名前の付されたグラフをラベル付きグラフと呼ぶ。例題１．１の炭素原子の問題ではラベル無しで数を数えたが、ラベルを付けると別個のきとして扱うようになる

連結グラフ

一言でいえば、１つにつながっているグラフ。定義的には
グラフGの点u, vに関して、G に u, v を結ぶ道があれば、uはv に連結されるという。
グラフＧを構成する任意の点において、ＶiをＧの部分集合とすると、
　　u は v に連結される　⇔　u は v と同じＶに属する
となる。
各集合からなる部分グラフをＧの成分とよび、成分数が１のものを連結グラフという。

次数および次数列

・点v の次数
v に接続している辺の本数。ただし、ループの場合は２本とカウントする。
式では deg(v) となる
・孤立点
次数ゼロの点
・端点
次数１の点
・次数列
次数を増加順に記したもの。同じ数字が繰り返すことがある
e.g. (1,1,1,3,3,4,5)
・握手補題
任意のグラフのすべての点の次数の合計は必ず偶数になる
・グラフ的
整数列 (d1, d2, …dn)が与えられたとき、n 個の点からなるGに対し、
　　deg(vi) = di
が成り立つとき、整数列はグラフ的であるという

部分グラフ

グラフGの部分グラフ・・・点がすべてV(G）に属し、変もすべてE(G)に属するもの。
グラフGの点と辺の除去、縮約によってGの部分グラフを作ることができる

行列によるグラフの表現方法

V = { 1, 2, …n } , E = { 1, 2, …m } とした場合、
隣接行列・・・点i, j を結ぶ辺の本数を ij 要素とする n × n の行列
接続行列・・・点i と辺 j が接続している場合 ij 要素を１とし、していない場合は０とした n × m の行列（ループの場合も１としている。２とする資料もある）

重み付きグラフ

各辺に重みがつけられたグラフ。
この場合の隣接行列の各要素は辺数の和ではなく重みを付けた辺数の和になる

例題

例題2.1～2.4

2.1.1 グラフの次数列をかけ
(3,3,3,3)
2.1.2 隣接行列A及び接続行列Mを求めよM　

A = [
    0, 1, 1, 1
    1, 0, 1, 1
    1, 1, 0, 1
    1, 1, 1, 0
]
M = [
    1, 1, 0, 1, 0, 0
    0, 1, 1, 0, 1, 0
    1, 0, 1, 0, 0, 1
    0, 0, 0, 1, 1, 1
]

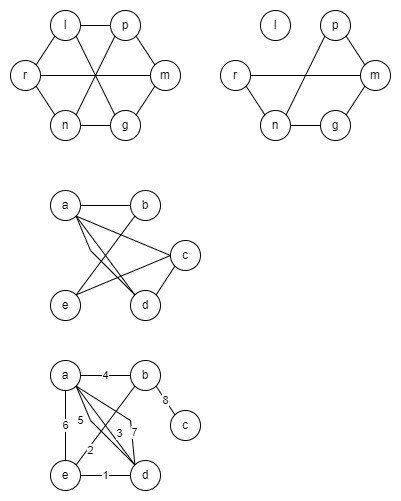
2.2.1  図の G1 と G2 の間の同形写像 φ, θ を見つけよ。また, G1 の任意の辺 e 及び点 u, v に対して ψG1 (e) = uv ⇔ ψG2 (φ(e)) = θ(u)θ(v) が成り立っていることを 2,3 の {e, u, v} の組に対して確かめよ.
θ(a) = 1, θ(b) = 2, θ(c) = 3, θ(d) = 4, θ(e) = 5
φ(ab) = 12, φ(bc) = 23, φ(cd) = 34, φ(de) = 45, φ(ae) = 15, φ(ce) = 35
2.2.2  図 2.16 のグラフ G2 の部分グラフを 2 つ挙げよ.
2.2.3  .次の隣接行列 A, 接続行列 M で与えられるグラフをそれぞれ描け

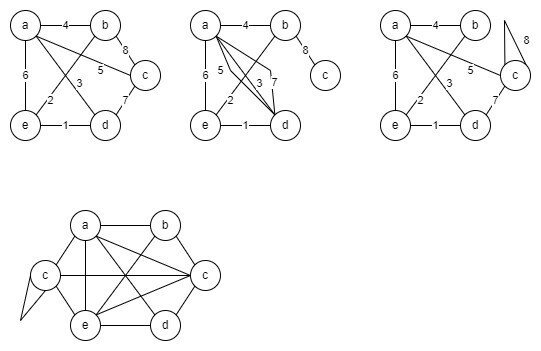
2.3.1 5 個の点と 8 本の辺をもつ次のようなグラフを描け
2.3.2 図に与えられるグラフの隣接行列 A, 接続行列 M を求めよ.

2.3.3 6 点からなるグラフで, 各点の次数列が (3, 3, 5, 5, 5, 5) であるものを描け. この次数をもつ単純グラフは存在するか ?
存在しない

2.4.1 講義ノート #1 の例題 1.3 (2) の解答に載せた図の二部グラフの隣接行列と接続行列, 及び次数列をそれぞれ求めよ. ただし, 接続行列を求める際には, 各自がどのように各辺に番号をふったのかを明示して解答を作成すること.
点には左上から右に向かって順に１～、辺には紐づいている頂点が若く、かつ左側から順に１～として番号を振る

2.4.2 次数列 (3, 3, 3, 3, 3, 3) はグラフ的か ? 理由とともに答えよ
ずのようなグラフが存在するため、グラフ的である
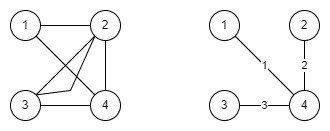
2.4.3 例題 2.2 の 1. にならって図 2.25 に載せた 2 つのグラフ G1, G2 の同形写像 θ, φ を見つけ, G1 の任意の辺 e 及び点 u, v に対して ψG1 (e) = uv ⇔ ψG2 (φ(e)) = θ(u)θ(v) が成り立っていることを {e, u, v} の組に対して確かめよ.

θ(a) = 1, θ(b) = 2, θ(c) = 3, θ(d) = 4
φ(ad) = 14, φ(ab) = 12, φ(ac) = 13, φ(bd) = 24, φ(cd) = 34, φ(bc) = 23
ψG1(ad) = ad　⇔　ψG2(φ(ad)) = ψG2(14) = 14 = θ(a)θ(d)
ψG1(ab) = ab　⇔　ψG2(φ(ab)) = ψG2(12) = 12 = θ(a)θ(b)
以下略

例題2.5

a
グラフ G の任意の 2 点 u, v 間の距離を d(u, v) とする. 今, 点 u を固定し, v (= u) を任意の G 内の点とするとき, d(u, v) の最大値を点 u からの最遠距離と定義し, e(u) と書くことにする. また, G 内の全ての点 u に対する e(u) の最小値をグラフ G の半径と呼び, R(G) と書く. さらに, 全ての u に対する e(u) の最大値を G の直径と呼び, D(G) と書く. また, 半径に等しい最短距離を持つ点の集合を G の中心と呼び, 最遠距離を持つ点の集合を G の周辺と言う. これを参考にして図 2.28(右) のグラフの各点の最遠距離, 半径, 直径, 中心, 及び, 周辺を求めよ
e(1) = 3, e(2) = 2, e(3) = 2), e(4) = 3, e(5) = 2, e(6) = 2
R(G) = 2, D(G) = 3
中心 = {2, 3, 5, 6}, 周辺 = {1, 4}

b
A をグラフ G の隣接行列とするとき, 次の和 :
S(r) = A + A2 + A3 + ··· + Ar = r k=1 Ak
の要素 [S(r)]ij は点 i から点 j に至る長さ r 以下の歩道の総数であることを図 2.28(右) のグラフ G の例を用いて示せ. また, (2.21) 式で r の値を 1 から徐々に増やしていったとき, S(r) の非対角要素が全て非ゼロになったときの r の値は, 例題 2.5-a で述べた直径 D(G) になっていることを図 2.28(右) の G に対して示せ

 A = [
    0 1 0 0 0 1
    1 0 1 0 0 1
    0 1 0 1 1 1
    0 0 1 0 1 0
    0 0 1 1 0 1
    1 1 1 0 1 0
 ]

A2 = [
    2 1 2 0 1 1
    1 3 1 1 2 2
    2 1 4 1 2 2
    0 1 1 2 1 2
    1 2 2 1 3 1
    1 2 2 2 1 4
]

A3 = [
    2 5 3 3 3 6
    5 4 8 3 4 7
    3 8 6 6 7 9
    3 3 6 2 5 3
    3 4 7 5 4 8
    6 7 9 3 8 6
]

A + A2 = [
    2 2 2 0 1 2
    2 3 2 1 2 3
    2 2 4 2 3 3
    0 1 2 2 2 2
    1 2 3 2 3 2
    2 3 3 2 2 4
]

[0][0] = 2, 1から1に行く、長さ２以下の道　1->2->1, 1->6->1 = 2
[0][1] = 2 1から2に行く、長さ…　　　　　1->2, 1->6, 2 = 2
…
[2][2] = 4, 3から3に行く、…　　　　　　　

A3のとき非対角成分がすべてゼロ出なくなるので、S(r)もA3の時にすべてゼロでなくなる。
よって、D(G) = r = 3

c
例題 2.5-b での S(r) の代わりに, η を η ≥ 1 の定数として
W(r) = A η + A η 2 + A η 3 + ··· + A η r = r k=1 A η k
を考える. 例えば, これは図 2.28(右) のグラフ G が地下鉄の路線図であるとするならば, 「近い駅間ほど乗客の利用頻度 (価値) が高い」などのように現実の問題と関連させ, 意味づけすることができる. さて, この行列 W(r) に対し Cr(i, r)=[W(r)]1i + [W(r)]2i + ··· + [W(r)]ni = n j=1 [W(r)]ji (2.28) を点 i における長さ r のターミナル容量と呼ぶ.2.28(右) のグラフ G の各点に対して長さ 2 のターミナル容量を求めよ. ただし, η = 6 とする. また, 図 2.28(右) のグラフを地下鉄の路線図と考えた場合, ここで得られた結果は何を意味するか, を簡潔に述べよ

※e.g. Wr = [[ 1, 2 ][3, 4]]のとき、
C(1, r) = 1 + 3, C(2, r) = 2 + 4 になる

長さ２のターミナル容量は

(A + A2) / η2 = [
    2 7 2 0 1 7
    7 3 7 1 2 8
    2 7 4 7 8 8
    0 1 7 2 7 2
    1 2 8 7 3 7
    7 8 8 2 7 4
] / η2

より、C(1,2) = 19 / 36, C(2, 2) = 28 / 36, C(3, 2) = 1,
C(4, 2) = 19 / 36, C(5, 2) = 28 / 36, C(6, 2) = 1
近い駅間ほど利用頻度が高いとしたとき、各駅の乗客量を定量的に表したものになる

d
図 2.28(右) のグラフの各辺に図 2.29 のような重みをつける. この重みは地下鉄の各区間の「非混雑度」を表すものとし, この値が大きなほど, 客は快適に乗車することができる. このように各辺が「重み付け」されたグラフを重み付きグラフと呼ぶが, この重み付きグラフの場合には隣接行列 A の各要素 [A]ij は i, j 間の辺数ではなく, 重みを付けた辺数の和となる. これをふまえて, 図 2.29 の重み付きグラフ G に対して隣接行列 A を求めよ.

 A = [
    0    0.6 0    0    0   0.16
    0.6  0   1    0    0   0.5
    0    1   0    0.76 0.6 0.06
    0    0   0.76 0    0.3 0
    0    0   0.6  0.3  0   0.3
    0.16 0.5 0.06 0    0.3 0
 ]

e
例題 2.5-d での隣接行列に対し, X ≡ A/η とおこう (η = 6). このとき, 図 2.22 のグラフ G に対し X∞ = limr→∞ Xr = 0 (ゼロ行列) (2.32) となることを示せ

Aの i, j 要素は
[Ar ]ij = 6 Σ 6 Σ ··· 6 Σ Ail1Al1l2Al2l3 ··· Alr−2lr−1Alr−1j
となり、行列Aの要素がすべて１の時には
[Ar ] ij = 6 Σ 6 Σ ··· 6 Σ = 6 r-1　となる
今回の行列は要素が１以下であるため、Rを１以上の実数として
[Ar ] ij = 6 Σ 6 Σ ··· 6 Σ Ail1Al1l2Al2l3 ··· Alr−2lr−1Alr−1j <= 6 r-1(1/R)r
rの極限を取ると、X = 0

f
I =( I + x + x2 + …) - (x + x2 + …)
= (I -x) + (I -x)x + (I -x)x2 + …
= (I -x)(I + x + x2 + …
I / (I -x) = I + x + x2 + …
Σx = (I -x) -1 - I

W∞ = (I -x/6) -1 - I
=

    0.011703 0.107357 0.018968 0.002594 0.003841 0.036307
    0.107357 0.048703 0.181174 0.024148 0.023988 0.093265
    0.018968 0.181174 0.059699 0.139956 0.114564 0.031928
    0.002594 0.024148 0.139956 0.020997 0.065383 0.006750
    0.003841 0.023988 0.114564 0.065383 0.017431 0.054118
    0.036307 0.093265 0.031928 0.006750 0.054118 0.011765

g
ターミナル量を求める

    c1 = 0.180770
    c2 = 0.478635
    c3 = 0.546288
    c4 = 0.259827
    c5 = 0.279325
    c6 = 0.234132
１がもっともターミナル量が低くなっている＝非混雑度が低い
　=> 6-1間の路線を調整するのが一番いい

例題2.6 ～ 2.8

次のグラフを描け
2.6.1  隣接行列 A :
A = [
    0101
    1021
    0201
    1110
]


2.6.2  接続行列 M :
M = [
    100
    010
    001
    111
]

2.6.3
各点に接続している辺の数
2.6.4
各点に接続している辺の数
2.6.5
２で固定

2.7.1 省略
2.7.2
可能な辺の本数はn 点の中から任意の２点を選ぶ方法の数なので
m = nC2 = n(n-1) / 2
（可能な辺の本数 = 選べる辺の種類）

総数をNとすると、グラフの総数は 1, 2, … m本の辺を選んだ時の総和になるので
N = mC0 + mC1 + … mCm = ΣmCk ・・・①

2項定理の左辺を a, b = 1 とすると
(1 + 1 ) n = 2x = ΣnCk　・・・②

①、②を比較し
N = 2x = ΣxCk = ΣmCk
= 2m = 2^(n(n-1)/2)

2.8.1 (3, 3, 3, 3, 3, 3, 3, 3, 3, 3)はグラフ的か? 理由とともに示せ. また, このグラフの隣接行列, 接続行列を書け.

A = [
    0 1 0 0 0 1 0 0 0 1 // a
    1 0 1 0 0 0 1 0 0 0 // b
    0 1 0 1 0 0 0 1 0 0 // c
    0 0 1 0 1 0 0 0 1 0 // d
    0 0 0 1 0 1 0 0 0 1 // e
    1 0 0 0 1 0 1 0 0 0 // f
    0 1 0 0 0 1 0 1 0 0 // g
    0 0 1 0 0 0 1 0 1 0 // h
    0 0 0 1 0 0 0 1 0 1 // i
    1 0 0 0 1 0 0 0 1 0 // j
]

M = [
 // 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5
    1 0 0 0 0 0 0 0 0 1  1 0 0 0 0 // a
    1 1 0 0 0 0 0 0 0 0  0 1 0 0 0 // b
    0 1 1 0 0 0 0 0 0 0  0 0 1 0 0 // c
    0 0 1 1 0 0 0 0 0 0  0 0 0 1 0 // d
    0 0 0 1 1 0 0 0 0 0  0 0 0 0 1 // e
    0 0 0 0 1 1 0 0 0 0  1 0 0 0 0 // f
    0 0 0 0 0 1 1 0 0 0  0 1 0 0 0 // g
    0 0 0 0 0 0 1 1 0 0  0 0 1 0 0 // h
    0 0 0 0 0 0 0 1 1 0  0 0 0 1 0 // i
    0 0 0 0 0 0 0 0 1 1  0 0 0 0 1 // j
]

(2) 完全 2 部グラフ K3,3, K4,4 を異なる 2 通りに描き, その両者が同型であることを例題 2.2 の 1. に従って示せ.
略

この記事が気に入ったらサポートをしてみませんか？