
広島大学 理学部数学科 平成28年度編入学試験 第5問
問題はこちら。

線形代数の問題です。小問(1)、(2)は基本的な問題です。(3)は前問とは全く独立した問題ですので、
ノーヒントで対応する必要があります。複数の数列を同時に評価するのは大変なので、R^3が内積空間であることを利用しましょう。
ベクトルy、zに直行するベクトルを1つとれば、内積を取ることで、a_n・xだけ残り数列が個別に評価できることがわかります。
(4)はAは3つの異なる固有値を持つので、各固有値に対応する固有ベクトル同士は1次独立です。
したがって、3つの固有ベクトルは基底となります。
この固有ベクトルを基底にとり、極限を考える問題は頻出ですのでしっかり押さえておきましょう。
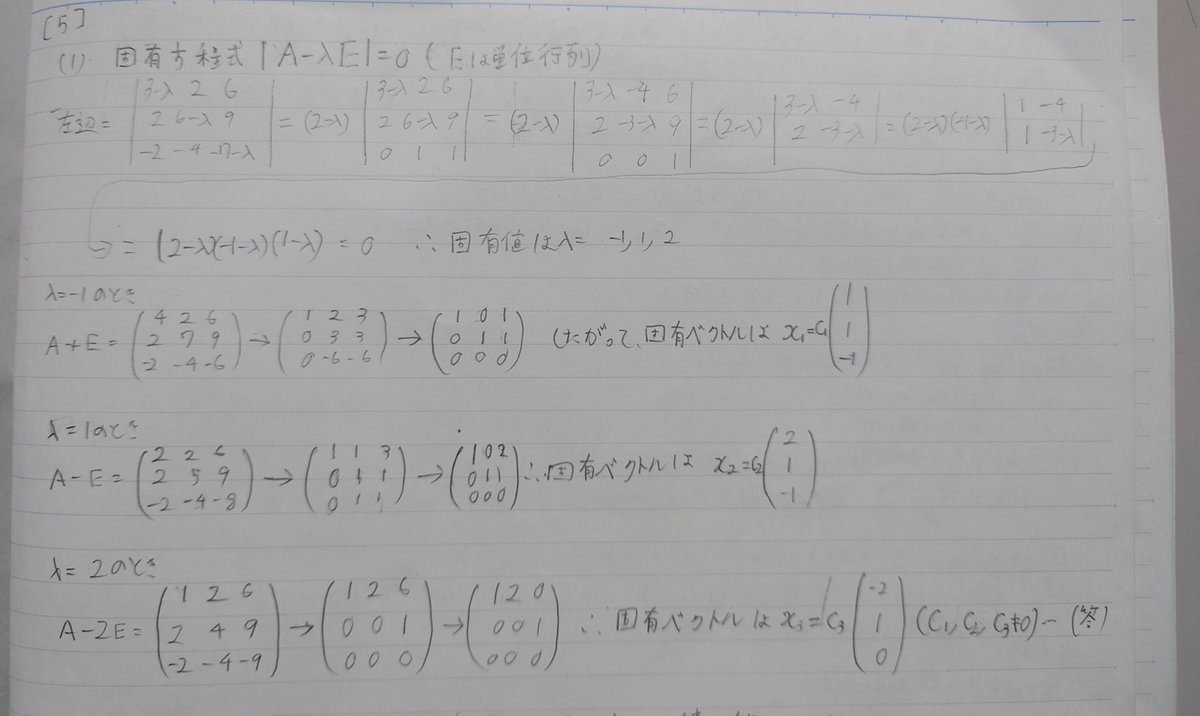



(3)は結構、骨のある問題ではなかったでしょうか?
広島大学数学科編入試験の解答22年分(平成16年〜令和6年)ありますので、ご参考にして頂ければ幸いです。ただし、第三者からの校正等はありませんので間違いが含まれる場合もあります。ご了承ください。
この記事が気に入ったらサポートをしてみませんか?
