Geometric Betsize (幾何級数的bet)

今回は中級者～上級者に向けてGeometric betsize(ジオメトリックベットサイズ)と呼ばれる概念について話していきたいと思います。
pokerにおいてbetsizeというのは非常に難しく、多くの人が
バリューターゲットに対してどの程度callをもらえるか
ブラフターゲットに対してどの程度Foldをもらえるか
ということを考えてbetしているかと思います。

このようなsize構成はExploit的な観点としては優れており、バランスの取れていない相手に対して有効です。
しかしながらバランスの取れている相手に対してbetsizeを考える際には、自身の持つハンドと相手の持ちうるハンド(レンジ)からではなく、相互のレンジを考えてbetしていくことで、EVを獲得することが必要となってきます。

今回は、簡単な例から考えていき、最終的にGeometric betsizeと呼ばれる非常に有益なbetsizeの構成について理解を目指します。

前提として以下のnoteをあらかじめ読んでいただくとよいかと思います。

注意点です。この記事は以下のことを心に留めて読むようにしてください。

・数式的な処理は興味のある人はよく読み、一般的なpoker playerや、数字が苦手な人はその計算によって得られる結果をしっかりと把握すること。

・最終的な結果と、その結果を使うことができる条件をしっかりと意識して、覚えること。

・各結果について、自身が理解していることを確認してから次の項目へと進むこと

人によっては少し重たい記事ですが、pokerへしっかり取り組もうとする場合には不可欠な概念を紹介いたしますので腰を据えて読んでいただけると嬉しいです。

・AKQgame詳解

・AKQgame bet可変

先述した過去記事においてAKQgame(千里眼ゲーム)の解説をしました。
該当記事内での前提と導出、結論はどのようなものだったでしょうか？

・前提
betはallinのみ
ポラライズドvsコンデンスド
・導出
無差別の原理に基づき、適切なブラフ頻度(アルファという概念)や適切なcall頻度(MDF)を考え、EVを計算した。
・結論
ポラライズド側はNutsのすべてをバリュー、Air(EQ0)の一部をブラフして、コンデンスド側は適切な頻度(MDF)でcallする

問題ないでしょうか？

今回の主題はベットサイズについてですから、
・前提
betはallinのみ
を
・betsizeは自由
と変更して考えてみましょう。
potをp　betsizeをb　とします。

この場合、allin以外のbetを受けるとKKはルール上レイズをすることができますね。
しかしながら、もしKKでレイズをすればAAにはコールされ、QQにはfoldされます。
KKでbetをしてはいけないように、ブラフキャッチハンドでポラライズにレイズをすることは損をするだけですから、レイズは被支配戦略となります。

では、レイズをされないとき、bettor側はどのサイズでベットすることがよいのでしょうか？

どのようなサイズでbetをしても相手はMDFでcallしてきます。
すなわち、こちらのブラフハンドEVを0にするようにcallしてくるのです。
よってAAのEVがそのままポラー側のEVとなります。

(なぜなら
polar側EV = 1/2*QQでのEV + 1/2*AAでのEV = 0+1/2*AAでのEV
ですから。(頻度も考慮))

AAでは
callされたときにpot+betを
foldされたときにpotを
獲得できるので

AAでのEV 
= (p+b) * (相手のcall頻度)+p*(相手のfold頻度)
=(p+b)*MDF+p*(1-MDF)
=p + pb/(p+b)
=p*(p+2b)/(p+b)
(ここでMDF = p/(p+b))

Graph1

グラフで見ると確かにbetsize=potでEV75となっており、
betsizeが大きくなるほどEVは上昇するが、増加率は下がっていきます。
(数学ができる人はEVをbで2階まで偏微分してください)

次にバリューハンドの割合が変わった場合を考えていきましょう。
現在polar側は
AA(Nuts)とQQ(Air)を等しく持っていますが、AAのほうが多い場合や
QQのほうが多い場合を考えます。
少し考えてみて下さい。

ポラライズの記事を振り返ればわかりますが、
バリューは全ハンドbetです。
そしてbetsizeによりバリューブラフ比率やMDFが決まります。
(レンジ全体のバリュー比率が小さくともこれらは変わりません。)

何が変わるかというと最終的な期待値が変わります。
AAの比率をxとすると
polar側EV = (1-x)*QQでのEV + x*AAでのEV = x*p*(p+2b)/(p+b)
となりxに比例します。
よってバリューがおおければ期待値は上昇します。

よって我々にとって、なるべく大きなサイズでbetをする。すなわちallinをするというのがこのモデルでの最適な戦略となります。

纏めましょう。

リバーでの(Polar側から一回しかbetできない場合の)最適戦略は、
・Nutsのすべてと適切なブラフをallinすること
となる。

次のように考えると面白いかもしれません

polar側EV = (1-x)*QQでのEV + x*AAでのEV
であり、QQのEVは0なので
相手がブラフキャッチを適切なハンドで行い、AAというバリューに放銃するとき、Polar側はチップを獲得できることがEVになっている。

すなわち、
相手にコールさせるほど
つまり
自身に多くのブラフを含められるほど
EVは上昇するので、なるべく大きなbetsizeを用いるのがよい。

・マルチストリートAKQ概観

さて、では今回は少し実践に近づけて、AKQゲームの形式を引き継いだままベッティングラウンドを複数に分けてみましょう。
つまりポラー側はbetにコールをもらった後にもう一度betをすることが可能なわけです。

絶対にラグしか落ちないTurn-Riverを想定していただければよいかなと思います。

設定を書いておきます。

Pot = 100
Stack = 400
Hero A or Q 
Villain K

ボードはなくベットは2回できる。
betはallinまで可能。

K側はベットもレイズもしないことは感覚的にわかるでしょう。
AQ側は最後のベットでallinすることになるのはすでに分かっています。
つまり、持っているスタックを2回あるベットラウンド(わかりやすく以下Turn,Riverと呼びましょう。)でどのように分けてallinに向かうのがよいかという議論になります。

つまりこう言ってもいいです。
どのようなサイズ(比率)で2回打ってallinする場合にブラフを最も含めることができるのか。

基本的にbetをするときはpotの%で考えることが多いと思いますので今回もそう考えましょう。
例えばTurnで100%betをするとpotは300%に膨らみ、
Riverでもう一度100%betをするとさらに300%へと膨らみます。
そしてちょうどオールイン(900%)となりますね。

逆に、Turnで200%betを行い500%へと膨らませ、Riverで40％betを行い180%に膨らませることで最終的にallinという選択肢もあります。

このようにpotの成長率をr1,r2としましょう。
今回は
r1*r2 =9
となりますね。

横軸r1に応じて含められるブラフハンドの数は上のように変化しr1=3,r2=3で最大をとります。

すなわち、

2度同じサイズを用いてallinまで入れきるbetsizeを用いるとき
ポラライズは最大の期待値を得ることができる。

のです。このようなベットサイズの構築をGeometric betsizeと呼びます。

・Geometric betsize

この概念はポラライズの基本です。
完全なポラライズEQ100 or EQ0でターンカードやリバーカードによってEQが変化しない場合はこのようなサイジングを使用するべきです。

以下の図は代表的なシチュエーションでのGeometric sizeをまとめた表になります。
(表の算式で絶対参照を忘れており、一部数値が誤っていました。
2022/9/8に訂正いたしました
大変申し訳ありません。保存などしていた方は再度ご確認ください。
またご指摘いただいた方に心よりお礼申し上げます。)

拡大図

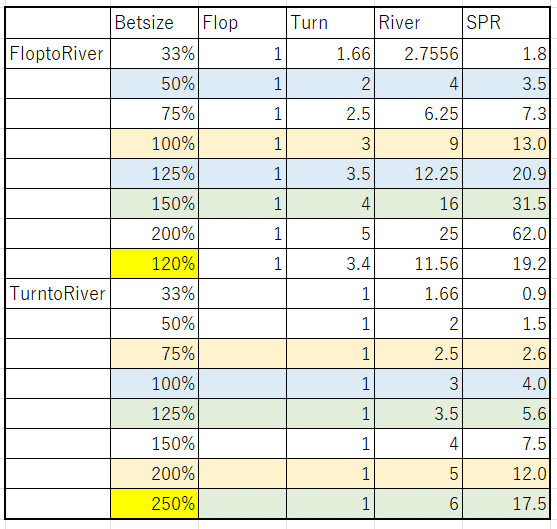
たとえばFlopでSPRが17.7の場合、(BBcallのSRPなどはこうなりますね!)
拡大表では115%betでリバーまで行くとSPR17.5が入りきるといっています。

つまり、Flopからポラライズをしたいときは125%程度のbetを三回打つことになります。
例としてポラライズできそうなAK6rのボードを考えてみましょう

Flopで、AKtwopairのような強いハンドでは確かに125%betが採用されていますね！Turn-RiverもGeometricに継続することになります。

Flopチェックした場合のdelay-CBでは新たに刺さったセットなどを用いてTurn-Riverでポラライズをしています。
この時は250%sizeが使用されており、これもGeometricsizeです。

(3回で入れきるGeometricsizeを3e,2回で入れきるGeometricsizeを2eと呼んだりします。)

今度はBTNvsUTGの3betpotにおいて見てみましょう
Geometricはいくつですか？
SPRが5.6ですから、65%弱のbetとなります。

Wizardでは65%サイズが選択肢にはないので75%が使用されていますね。
特徴的なのは125%sizeが使われなくなっていることです。
GTOでもGeometricが意識されていることがわかりますね！

・最後に

いかがでしたか？
かなり大変だったかと思いますが、Geometricという概念の意義と導出の仕組みを理解いただけたのではないかと思います。

導出部分が難しかった方も、最後の結果だけでも意識して、bet sizeを考えてみてはいかがでしょうか？

よく、
大きいsizeはpotoverという発想の方や
RiverでSPRを1にすべきと言う意見
を耳にしますが、
ポラライズの基本はGeometric
です。

このことを念頭にGTOに向き合うと新たな発見があるのではないかと思います。

Twitter上でたくさんの方にフォローいただいています。いろいろ呟いてますのでもしよろしければお願いします。

アミューズや勉強会等、様々な場所にお呼び頂くことも増え、とても充実したポーカーができています。関わってくださっている方に感謝申し上げます。

noteでもお布施をとても多くの方にいただき、サポートをしてくださる方もいらっしゃいます。非常にモチベーションになり、助かっています。
今の状況が無ければ記事の執筆を続けていないかもしれません。
スキやフォロー、拡散だけでも構いませんので、余裕のある方はサポートいただけると嬉しいです。

今回の記事を書くにあたり、自身でも数学的な導出を整理してみました。
「意外と面倒で、整理したはいいけど興味のある人がいるのだろうか？」
「寧ろこれを書くと難しい記事と思われるだけではないか？」
と言う不安が頭をよぎり、割愛しました。
しかしながら日本語でそれなりに導出をしているところはかなり少なそうですので、
「数学的な話が気になる！！」
「導出のない結果なんて使えない！」
という特異な方向けに有料部分で導出をしています。興味のある方はご購入ください。
自身で導出できる方や既に数式が辛かった方は不要な内容かと思いますので、気が向いたらお布施してください笑
上述の理由から有料部分にしましたが、金額は高くしたくなかったので2e sizeにあやかって250円です。

以下有料部分