ラビットチャレンジレポート:ステージ4 深層学習 day3
1. 再帰型ニューラルネットワークの概念
1-1 要点
■RNNとは
時系列データに対応可能なニューラルネットワーク。
時系列データとは、時間的順序を追って一定間隔ごとに観察され、相互に統計的依存関係が認められるようなデータの系列。
例)音声データ、テキストデータ等
時系列モデルを扱うために、RNNは初期の状態と過去の時間t-1の状態を保持し、そこから次の時間tでの出力を再帰的に求める再帰構造を持つ。
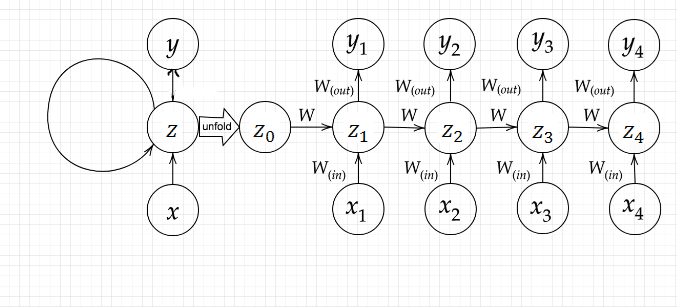

上記のように、RNNでは$${z^{t-1}}$$が出力$${y^{t-1}}$$と次の$${z^t}$$への入力として使われる。これにより、過去の状態が隠れ層に保持されることになる。
■BPTT
RNNにおけるパラメータ調整方法の一種。
⇒誤差逆伝播法の一種。
調整すべきパラメータは$${W_{in},W_{out},W}$$の3つ。
BPTTの数学的な記述は以下のようになる。


パラメータの更新式は以下のようになる。

誤差関数は以下のようになり、誤差関数に直接渡された$${z^t}$$から遡っていくと過去の$${z}$$の情報がきちんと反映されていることが分かる。

1-2 実装演習
2進数の加算を行うRNNの動作を確認した。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
# def d_tanh(x):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number / 2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number / 2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[- t - 1], b_bin[- t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:, t + 1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t + 1] = functions.sigmoid(u[:, t + 1])
y[:, t] = functions.sigmoid(np.dot(z[:, t + 1].reshape(1, -1), W_out))
# 誤差
loss = functions.mean_squared_error(dd, y[:, t])
delta_out[:, t] = functions.d_mean_squared_error(dd, y[:, t]) * functions.d_sigmoid(y[:, t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:, t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t - 1], b_bin[-t - 1]]).reshape(1, -1)
delta[:, t] = (np.dot(delta[:, t + 1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(
u[:, t + 1])
# 勾配更新
W_out_grad += np.dot(z[:, t + 1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
W_grad += np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
W_in_grad += np.dot(X.T, delta[:, t].reshape(1, -1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index, x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.xlabel("count")
plt.ylabel("loss")
plt.show()結果、count4000回程度の学習で収束した。

------------
iters:9900
Loss:0.0008250850355093509
Pred:[0 1 1 1 1 0 0 1]
True:[0 1 1 1 1 0 0 1]
103 + 18 = 121
------------次に、初期値にXavierの初期化を使用した。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
# def d_tanh(x):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)/ (np.sqrt(hidden_layer_size))
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number / 2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number / 2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[- t - 1], b_bin[- t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:, t + 1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t + 1] = functions.sigmoid(u[:, t + 1])
y[:, t] = functions.sigmoid(np.dot(z[:, t + 1].reshape(1, -1), W_out))
# 誤差
loss = functions.mean_squared_error(dd, y[:, t])
delta_out[:, t] = functions.d_mean_squared_error(dd, y[:, t]) * functions.d_sigmoid(y[:, t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:, t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t - 1], b_bin[-t - 1]]).reshape(1, -1)
delta[:, t] = (np.dot(delta[:, t + 1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(
u[:, t + 1])
# 勾配更新
W_out_grad += np.dot(z[:, t + 1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
W_grad += np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
W_in_grad += np.dot(X.T, delta[:, t].reshape(1, -1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index, x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.xlabel("count")
plt.ylabel("loss")
plt.show()結果、最終的に収束はしたが、収束が遅くなった。

------------
iters:9900
Loss:0.005704115873360288
Pred:[0 1 0 1 1 0 1 0]
True:[0 1 0 1 1 0 1 0]
18 + 72 = 90
------------次に、活性化関数にReLU関数を使用した。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
# def d_tanh(x):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number / 2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number / 2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[- t - 1], b_bin[- t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:, t + 1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t + 1] = functions.relu(u[:, t + 1])
y[:, t] = functions.sigmoid(np.dot(z[:, t + 1].reshape(1, -1), W_out))
# 誤差
loss = functions.mean_squared_error(dd, y[:, t])
delta_out[:, t] = functions.d_mean_squared_error(dd, y[:, t]) * functions.d_relu(y[:, t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:, t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t - 1], b_bin[-t - 1]]).reshape(1, -1)
delta[:, t] = (np.dot(delta[:, t + 1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(
u[:, t + 1])
# 勾配更新
W_out_grad += np.dot(z[:, t + 1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
W_grad += np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
W_in_grad += np.dot(X.T, delta[:, t].reshape(1, -1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index, x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.xlabel("count")
plt.ylabel("loss")
plt.show()結果、勾配爆発により学習は収束しなかった。

最後に、活性化関数としてtanhを使用した。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def d_tanh(x):
return 1 - np.tanh(x)**2
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number / 2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number / 2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[- t - 1], b_bin[- t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:, t + 1] = np.dot(X, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t + 1] = np.tanh(u[:, t + 1])
y[:, t] = functions.sigmoid(np.dot(z[:, t + 1].reshape(1, -1), W_out))
# 誤差
loss = functions.mean_squared_error(dd, y[:, t])
delta_out[:, t] = functions.d_mean_squared_error(dd, y[:, t]) * d_tanh(y[:, t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:, t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t - 1], b_bin[-t - 1]]).reshape(1, -1)
delta[:, t] = (np.dot(delta[:, t + 1].T, W.T) + np.dot(delta_out[:, t].T, W_out.T)) * functions.d_sigmoid(
u[:, t + 1])
# 勾配更新
W_out_grad += np.dot(z[:, t + 1].reshape(-1, 1), delta_out[:, t].reshape(-1, 1))
W_grad += np.dot(z[:, t].reshape(-1, 1), delta[:, t].reshape(1, -1))
W_in_grad += np.dot(X.T, delta[:, t].reshape(1, -1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if (i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index, x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.xlabel("count")
plt.ylabel("loss")
plt.show()結果、収束しそうでしない。Tanhの導関数は最大値1になるので、シグモイド関数と比べるとやや勾配爆発気味になるのだろうか。

1-3 確認テスト
◆確認テスト①

回答①
現在の中間層から、次の中間層を定義する際にかけられる重み。
◆確認テスト②

回答②
(2)W.dot(np.concatenate([left, right]))
他の選択肢では、元の単語の情報が消失してしまう。
選択肢2の場合、一時的に要素数が2倍のベクトルになるが、そこに重みを掛けて元の要素数のベクトルに変換する。
◆確認テスト③

回答③

◆確認テスト④

回答④
$${y_1=g(W_{out}z_1+c)}$$
$${z_1=f(Wz_0+W_{in}x_1+b)}$$
より
$${y_1=g(W_{out}f(Wz_0+W_{in}x_1+b)+c)}$$
ただし、b,cをバイアス、fを活性化関数とした。
◆確認テスト⑤

回答⑤
(2)delta_t.dot(U)
2. LSTM
2-1 要点
RNNモデルにおいては、時系列を遡れば遡るほど勾配爆発または勾配消失が発生し、長い時系列の学習が困難になる。
この問題を解決したものがLSTMである。

LSTMは上図のように表される。
■CEC
LSTMでは、過去の入力、計算の結果を記憶するものとしてCECを導入している。ただし、CECは記憶はできるが学習はできない。
■入力ゲート・出力ゲート
CECに何を覚えさせるか、CECの記憶をどのように使用するかを学習する働きを持つ。
■忘却ゲート
CECは、過去の情報が要らなくなった場合でも削除することはできず保管され続ける。忘却ゲートは、過去の情報が要らなくなったタイミングで情報を削除する働きを持つ。
■除き穴結合
入力ゲート、出力ゲートは前回の入力、出力の値を元に次の入力出力の値への処理を決めている。覗き穴結合はCECの値も判断材料として使うための機能。
2-2 確認テスト
◆確認テスト①

回答①

◆確認テスト②

回答②
(1)gradient * rate
gradient * rate = gradient * threshold / normとなるので、normがthresholdを超えた場合に、gradientの大きさをnormで割ってthresholdを掛けることでthresholdの大きさにクリッピングしている。
◆確認テスト③

回答③
忘却ゲート。
必要のなくなった情報を削除する機能を持つのが忘却ゲート。
◆確認テスト④

回答④
(3)input_gate* a + forget_gate* c
CEC更新時の式、$${c(t) = i(t)*a+f(t)*c(t-1)}$$を表している。
2-3 関連事項
LSTMの学習について、動画講義では、通常のRNNと同じくBPTTでいいのか、それとも他の方法があるのか分からなかったので調べてみた。
こちらのサイトによると、05年頃、BPTTの枠組みで学習を進める手法が開発されたとあった。
また、講義中ではあまり忘却ゲートの重要性は分からなかったが、こちらのサイトによると、入力/忘却/出力ゲート・活性化関数等の要素をそれぞれ取り除いた場合の性能低下を見た場合、忘却ゲートと出力時の活性化関数が最も寄与しているとあり、考えている以上に重要な部品であることが分かった。
3. GRU
3-1 要点
LSTMでは、パラメータ数が多く計算負荷が高くなる問題があった。
これを改善したのがGRUである。GRUでは、パラメータを大幅に削減したため計算負荷が減少し、精度は同等またはそれ以上が望めるようになった。

隠れ層$${h(t)}$$に過去の状態を記憶しているのが特徴。
GRUではリセットゲートと更新ゲートが設けられている。
リセットゲートは前回の状態をどの程度保持するかを、更新ゲートは、前回の記憶と今回の記憶をどのような割合で使用するかを決める働きを持つ。
3-2 関連事項
GRUはLSTMの欠点を改善するため部品を減らしたものとのことだったが、それら部品の働きがどう変わったのか、分からなかったので調べてみた。
調べるに当たっては下記のサイトを参考にした。
・そもそもLSTMではhとCEC両方に過去の状態を保持していた。
よってまずこれをまとめた。
・忘却ゲートと入力ゲートの操作を1つにまとめた。
また、これらの変更に伴い、
・CECとhをまとめたため、出力ゲートによる出力制限は望ましくなく、出力ゲートの仕組みを取り除いた。
・出力ゲートがないと重み衝突が発生する可能性があるので、再帰経路上にリセットゲートを設けた。
まとめると、
・hとCECの機能をhに集約
・忘却ゲートと入力ゲートの機能を更新ゲートに集約
・出力ゲートをなくし、代わりにリセットゲートを置いた
4. 双方向RNN
4-1 要点
過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル。
文章の推敲、機械翻訳のように、ある時点までの過去の情報だけでなく、それ以降の未来の情報も同時に入力として得られる場合、過去の情報に加えて未来の情報も使用することで処理の精度を高めることができる。

4-2 確認テスト
◆確認テスト①

回答①
・LSTMの課題
パラメータ数が非常に多く、計算量が多くなってしまう。
・CECの課題
CECには学習機能がない。
◆確認テスト②

回答②
(4)(1-z) * h + z * h_bar
GRUにおける,出力層手前の隠れ層の更新式、$${z(t)*h(t-1)+(1-z(t))*h(t)}$$を表している。
◆確認テスト③

回答③
・LSTM
入力ゲート、出力ゲート、忘却ゲート、CECを持つ。
このためパラメータ数が多く、計算量が多い。
・GRU
更新ゲート、リセットゲートを持つ。
LSTMよりもパラメータ数が少なくなり、計算量も少なくなっている。
◆確認テスト④

回答④
(4)np.concatenate([h_f,h_b[::-1]],axis=1)
5. Seq2Seq
5-1 要点
Seq2seqとは、Encoder-Decoderモデルの一種。
時系列データを入力として取り、別の時系列データを出力とする。
■Encoder RNN

Encoder RNNの処理
・Taking
文章を単語等のトークンごとのIDに分割する。
例)昨日食べた刺身大丈夫でしたか。
→「昨日」「食べた」「刺身」「大丈夫」「でしたか」「。」
→「1」「2」「3」「4」「5」「6」(ID)
・Embedding
IDから、そのトークンを表す分散表現ベクトルに変換。
単語をOne-hotベクトルで表現すると、単語数分の要素数を持った配列を用意する必要がある。Embeddingではニューラルネットワークを用いて、One-hotベクトルをより要素数の少ない分散表現ベクトルに変換する。
・Encoder RNN
ベクトルを順番にRNNに入力していく。
最終的に得られた隠れ層$${h}$$にはそれまでに入力された情報が記憶されている。これをfinal stateとし、Decoder RNNに渡して、これに対応した時系列データを出力させる。
■Decoder RNN

Decoder RNNの処理
・Encoder RNNのfinal stateがDecoder RNNのinitial stateとして入力され、これをもとに最初の一語が選択される。
・ここで選ばれた単語を次のDecoder RNNへの入力とする。
・次の単語が選択される。
・これを繰り返し、得られた文字列を出力する
■HRED
Seq2seqでは一問一答の会話しかできず、文脈は無視される。
HREDは一文一文の過去の情報を記憶することで、過去の文脈を踏まえた文章を返すようになった。
■VHRED
HREDは、短いよくある答えを選ぶ傾向があった。
VDREDでは、潜在変数の概念を追加することでHREDの課題を解決した。
■VAE
入力データをより次元の小さい潜在変数zに変換した後、元のデータを復元して出力する構造を持ったネットワークをオートエンコーダと言う。zの次元が入力データより小さいため、次元削減を行っているものとみなせる。
VAEでは、潜在変数zが標準正規分布に従うと仮定することで、近い入力データ同士は近いベクトル(z)として表現されるように学習が進んでいく。
5-2確認テスト
◆確認テスト①

回答①
(2)
(1)は双方向RNN、(3)は構文木、(4)はGRUの説明である。
◆確認テスト②

回答②
(1)E.dot(w)
◆確認テスト③

回答③
・seq2seq2
時系列データから時系列データを作り出すモデル。
一問一答の会話しかできず、文脈は無視される。
・HRED
一文一文の過去の情報を記憶することで過去の文脈を踏まえた文章を返すようになった。
しかし、文脈に対して当たり障りのない回答しか生成しない傾向があった。
・VHRED
潜在変数の概念を用いて、上記HREDの課題を解決したモデル。
◆確認テスト④

回答④
確率分布
6. Word2vec
6-1 要点
単語のような可変長の文字列を固定長形式で表すための手法。
One-hotベクトルで単語を表現する場合、ボキャブラリの数と同じ要素数の配列が必要になるが、Word2vecではニューラルネットワークを用いて、これよりも大幅に少ない要素数のベクトルで単語を表現することができる。
7. Attention Mechanism
7-1 要点
Seq2seqでは、2単語でも100単語でも固定次元ベクトルの中に入力しなければならず、長い文章への対応が難しい。
Attention Mechanismは、文章が長くなるほど、そのシーケンスの内部表現の次元も大きくなっていく仕組みを持ち、入力と出力のどの単語が関連しているのかの関連度を学習する。
7-2 確認テスト
◆確認テスト①

回答①
・RNN
時系列データを処理するのに適したニューラルネットワーク
・word2vec
単語の分散表現ベクトルを得る手法
・seq2seq
1つの時系列データから別の時系列データを得るネットワーク
・Attention Mechanism
時系列データの中身に対して、それぞれの関連度に重みをつける手法
この記事が気に入ったらサポートをしてみませんか?
