度数の周波数比を計算する

事の発端

　読んでた音楽理論の本に「減5度音程の振動数比が45：64で複雑、長3度音程は4：5で簡単」って書いてた。
　じゃあ他の音程だとどうなの？って思って手計算した。

計算

平均律

　A4＝440Hzを基準にひたすら整数倍してった。

 n,   Hz, Tone
 1,  440, A4
 2,  880, A5
 3, 1320, E6
 4, 1760, A6
 5, 2200, C♯7
 6, 2640, E7
 7, 3080, G7
 8, 3520, A7
 9, 3960, B7
10, 4440, C♯8  //存在しない

　平均律だとA以外整数にならないから最も近い音を当ててる。

　平均律とは↓

平均律（へいきんりつ）（英: equal temperament）は、1オクターヴなどの音程を均等な周波数比で分割した音律。多種類が考案されている。西洋音楽で用いられる十二平均律がよく知られている。

十二平均律とは、1オクターヴを12等分した音律である。隣り合う音（半音）の周波数比は等しく$${\sqrt[12]{2} :1}$$（100セント）となる。

フリー百科事典『ウィキペディア（Wikipedia）』

　基準音に対して$${2^{\frac{n}{12}}}$$倍してけばいい。（nは基準音に対する半音の数）
　オクターブなら半音12個分だから2倍だよね～って感じ。

　完全5度のA5とE6の比は880：1320で2：3
　こんだけ簡単ならそりゃ安定するわなって感じ。

　長3度のA6とC#7の比は1760：2200で4：５
　これも簡単だし安定してる。

　つまりメジャーコードはルートに対して4：5：6の周波数で構成されてる。
　メジャーコードは全コードで一番安定してる。
（この辺の話は昨年度のアドカレに書いた気がする）

　次に出てきたのがG7だったけど、平均律だと3136Hzで50Hzくらいズレが生じてるから保留。
　一応書いとくけどルートとの距離は短7度で比は4：7

　次のB7は長2度でA7との振動数比は3520：3960で8：9
　テンションノートの9thですね。思ってたよりシンプルな比なんだなぁ。

　整数倍した周波数と平均律の差も載せとく

 n,   Hz, Tone, ETS,     diff
 3, 1320,  E6, 1318.51,  1.49
 5, 2200, C♯7, 2217.46, 17.46
 6, 2640,  E7, 2637.02,  2.98
 7, 3080,  G7, 3135.96, 55.96
 9, 3960,  B7, 3951.06,  8.94

　Aは言わずもがな差は0になるので省略

　440Hz基準だと10倍でピアノの鍵盤超えちゃうのでA1の55Hz基準でも一応計算してみたけど数がとんでもないことになりそうで辞めた。
　手計算でやるもんじゃない。

計算の残骸

純正律

　平均律だったら誤差出ちゃうけど純正律ならどうだろって思って同じようにやってみた。

　純正律とは↓

純正律（じゅんせいりつ Just intonation)は、周波数の比が単純な整数比である純正音程のみを用いて規定される音律である。

例えば純正律による長調の全音階は、純正完全5度（3/2）と純正長3度（5/4）を用いて各音が決定される。 すなわち、Cを基準とした場合、Cの3度上がE、5度上がG、次にGの3度上がB、5度上がD、さらにCの5度下がF、Fの3度上がAとなり、これらを1オクターヴ内に配列することでハ長調の全音階が得られる。

フリー百科事典『ウィキペディア（Wikipedia）』

　単純な整数比なんだから最初から純正律使えばよかったじゃん。

　とりあえず、さっきの表みたいに差を取る。

n,   Hz, Tone, JT,   diff
 3, 1320,  E6, 1320,  0
 5, 2200, C♯7, 2200,  0
 6, 2640,  E7, 2640,  0
 7, 3080,  G7, 3168, 88
 9, 3960,  B7, 3960,  0

　G7以外はぴったり数値が合いましたね。逆にG7の差は広がっちゃった。ここまで広がるなら12音階でルートに対して4:7の比の音はなさそう？

　流石に手計算でこれ以上やるのは拷問すぎるので、ここからはExcel君に任せる。

　まずExcel君に計算させてC8以上の周波数も出しておいて、440Hzの整数倍と一致するものをVLOOKUP使って探してあげた。Excelってほんと便利だなぁ…

結果がこれ

 n,   Hz, Tone
 1,   440, A4
 2,   880, A5
 3,  1320, E6
 4,  1760, A6
 5,  2200, C♯7
 6,  2640, E7
 8,  3520, A7
 9,  3960, B7
10,  4400, C♯8  //ここから存在しないゾーン
12,  5280, E8
15,  6600, G♯8
16,  7040, A8
18,  7920, B8
20,  8800, C♯9
24, 10560, E9
30, 13200, G♯9
32, 14080, A9
36, 15840, B9
40, 17600, C♯10
45, 19800, D♯10
48, 21120, E10
60, 26400, G♯10
64, 28160, A10

※どうでもいいですが人間の可聴域は大体20～20kHz

　とまぁここまで出しましたが、出てきた音は順にA, E, C#, B, G#, D#のみでした。Gはやっぱり出てこなかった。

　新たに出てきたG#はルートと長7度（短2度）で比が3520：6600で8：15
　なんか複雑になってきた気がする…！！

 　D#はルートと減5度で比が14080：19800で32：45
　今日一複雑なの来た！！！！

　16万Hzくらいまで計算させたが整数で一致したのはこの6つだった。じゃあ他の音の比はどうやって出してるの？って話がこちら。

注）ここからはわかりやすいように、基準音をCとする。

　まず今のところ分かっている整数比が下の図。

　ここでFはCの完全5度下なので、オク上の2に逆数掛けて$${2\times\frac{2}{3}}$$で$${\frac{4}{3}}$$

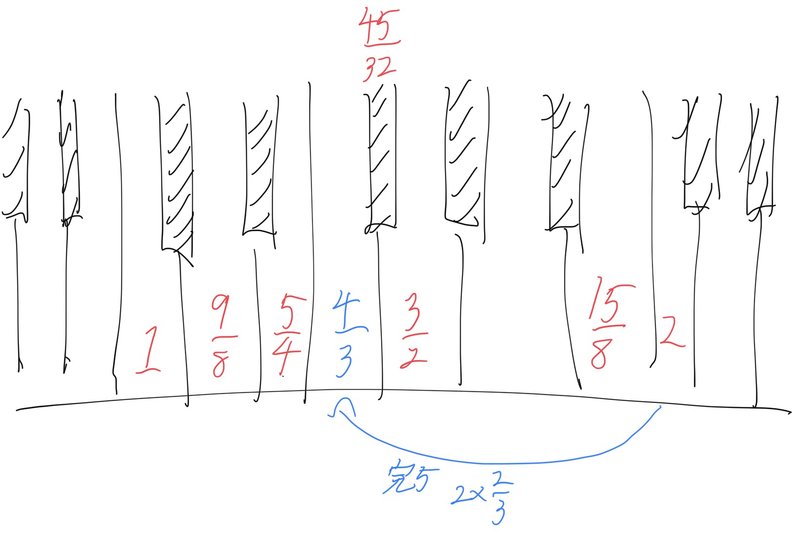
 AはFの長3度上なので$${\frac{4}{3}\times\frac{5}{4}}$$で$${\frac{5}{3}}$$

　こんな感じ。（Wikipediaの説明を図解しただけだけど…）
　黒鍵についても同様にやったのがこれ。

　一通り振動数比を計算してみたが、やっぱり一番複雑なのは減5度のトライトーン。ドミナントセブンスの緊張感はこういった複雑さから生まれる？

　次点で短2度かな。半音同士のぶつかりは確かにかなり濁って聞こえる。

コードの周波数比

ちょっと気になったからそれぞれのコードの周波数比も計算してみる。

Triad
C　　　 4：5：６
Cm 　　10：12：15
Csus2 　8：9：12
Csus4 　6：8：9
Caug 　20：25：32
(Cdim 　160：192：225)

4 Notes Chord
C7　　　 36：45：48：64
CM7 　　8：10：12：15
Cm7 　　90：108：135：160
CmM7 　40：48：60：75
Cdim7　 480：576：675：800

　見た感じmajorのDiatonic Chordは比が簡単め。（C, Csus2, Csus4, CM7）
　一番複雑なのはdim7。トライトーン2つもあるからそれはそう。
　個人的にaugとmM7が思ったよりシンプルだなぁって感じた。mM7がそんなに見ないのって比が中途半端すぎるからだったりするのかな？

　ちなみに分数augを四和音と捉えるなら比は288：324：405：512

まとめ

　今まで感覚で語ってた緊張感や安心感等の言葉を数学的なアプローチで説明できると凄く納得できるから、今後もこういうことやっていきたいね。

　あと平均律と純正律計算して思ったけど、近似されて生まれた周波数の濁りに気づかないくらいには人間の耳って貧弱なんだなぁと。今後は絶対音感ありますとか耳良いアピールしないようにしよ。