直列回路、並列回路

部品の2つの端子を持つ部品を数珠繋ぎに接続した回路を直列回路（series circuit）といいます。

直列回路では電流の経路が1つであり、同じ電流が各部品を順に流れます。
上の図では、R1とR2に流れる電流は同じになります。

2つの端子をそれぞれ互いに接続した回路を並列回路（parallel circuit）と呼びます。

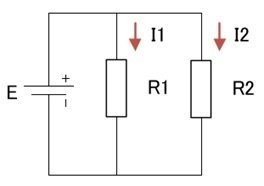
電流の経路が分岐して各部品に同じ電圧がかかります。

合成抵抗

複数の抵抗器を使用して電気回路を構成した際に、直列回路と並列回路で回路全体の抵抗値が変わります。このように複数の抵抗器で構成した回路全体の抵抗値を合成抵抗といいます。

抵抗の直列回路

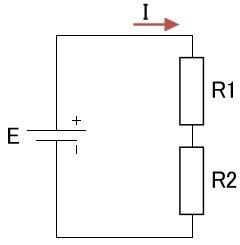
上の回路の合成抵抗は、オームの法則により、R=E/Iになります。
電流経路は一つなので、R1とR2には同じ電流が流れます。
従って、R1による電圧降下は、E1=R1×I、R2による電圧降下はE2＝R2×Iとなります。
電源電圧は、E＝E1＋E2になります。これを合成抵抗の式に代入すると

となり、抵抗器を直列に接続した場合、回路全体の抵抗値は、個々の抵抗値の合計になります。
例では2個の抵抗ですが、直列に接続されていれば、いくつでも抵抗値の合計が合成抵抗値になります。

抵抗の並列回路

下の図の回路を流れる電流は、R1とR2に分かれて流れますが、抵抗を通過したのちに合流するので、I=I1+I2で計算できます。

それぞれの抵抗に流れる電流は、抵抗値によって決まります。
抵抗値の逆数が電流の流れやすさを表し、コンダクタンスといいます。
R1、R2の端子は、同じように電源のプラスとマイナスに接続されているので、各々の抵抗器にかかる電圧は電源電圧と同じになり、以下の式が成り立ちます。

回路全体を流れる電流の式にオームの法則の抵抗の算出式を代入します。
それぞれの項にEを掛けると抵抗だけの式になります。
この式は、コンダクタンスを算出する式なので、両辺を逆数にすると並列接続の合成抵抗が算出できます。

多くの抵抗の並列回路でも、それぞれの抵抗のコンダクタンスの合計を算出し、逆数にすることで並列回路の合成抵抗値を算出することができます。