大海物語4スペシャル・閉店前の遊タイム期待値(天井期待値)を出しました！

ども、くろっくです。

今回は、大海物語SPの閉店前の天井期待値を出しました。

閉店前はどのくらい時間から攻めれるのか？

1k/17.18.19.20回転の4種類

残150～50分

以上の条件で計算してみました。

まずは最初に、普通の天井期待値をご覧ください。

通常の遊タイム期待値①
(1435玉-確変+時短△0.5玉-遊タイム△0.7玉)

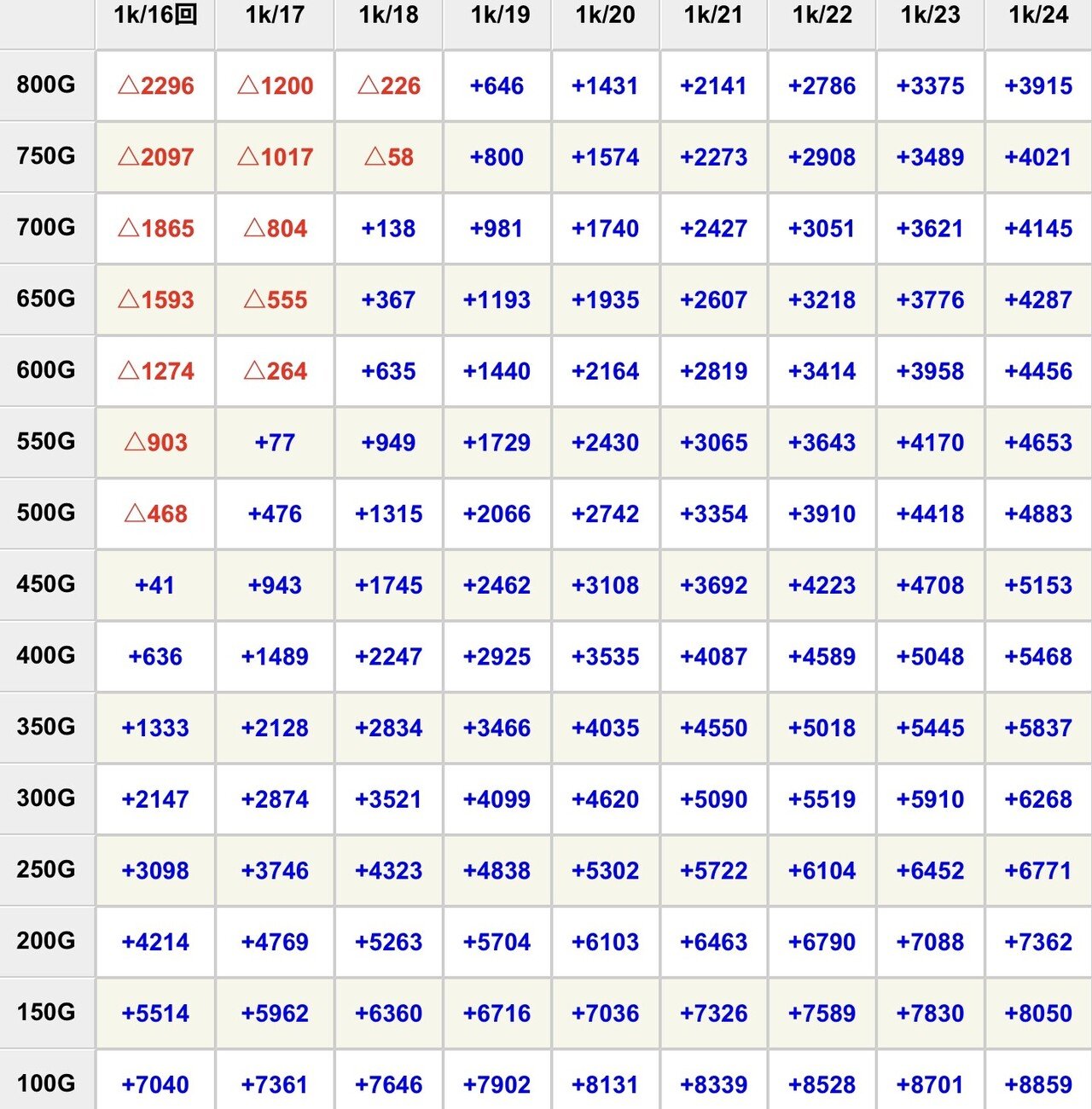
残保留4個・欠損保留5個。
欠損保留は「遊タイム残り3Gから欠損0個」「それより前の当選は全て欠損5個」と仮定する。

通常の遊タイム期待値②
(1420玉-確変+時短△0.75玉-遊タイム△1.0玉)

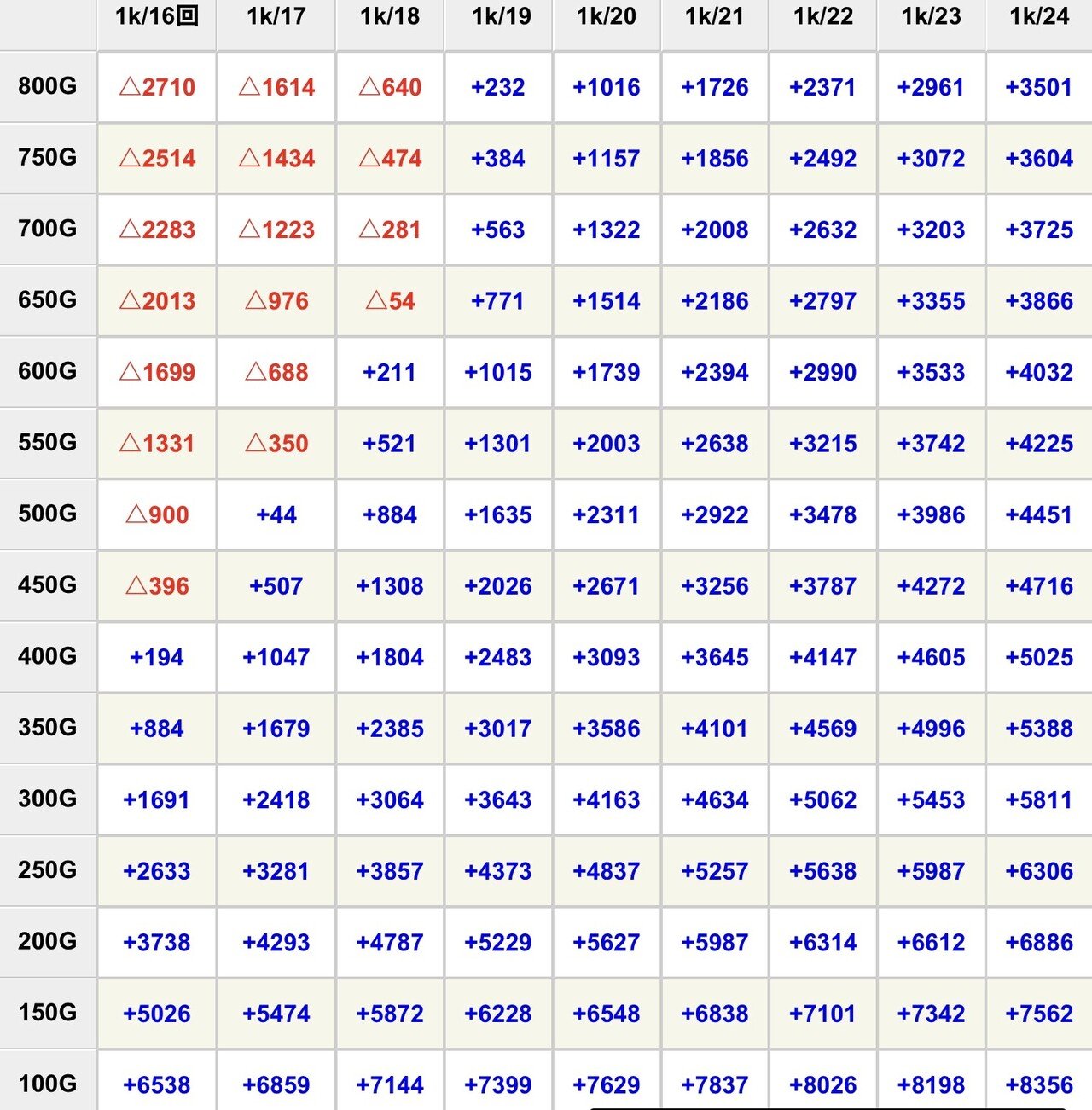
残保留4個・欠損保留5個。
欠損保留は「遊タイム残り3Gから欠損0個」「それより前の当選は全て欠損5個」と仮定する。

1台あたりの消化時間

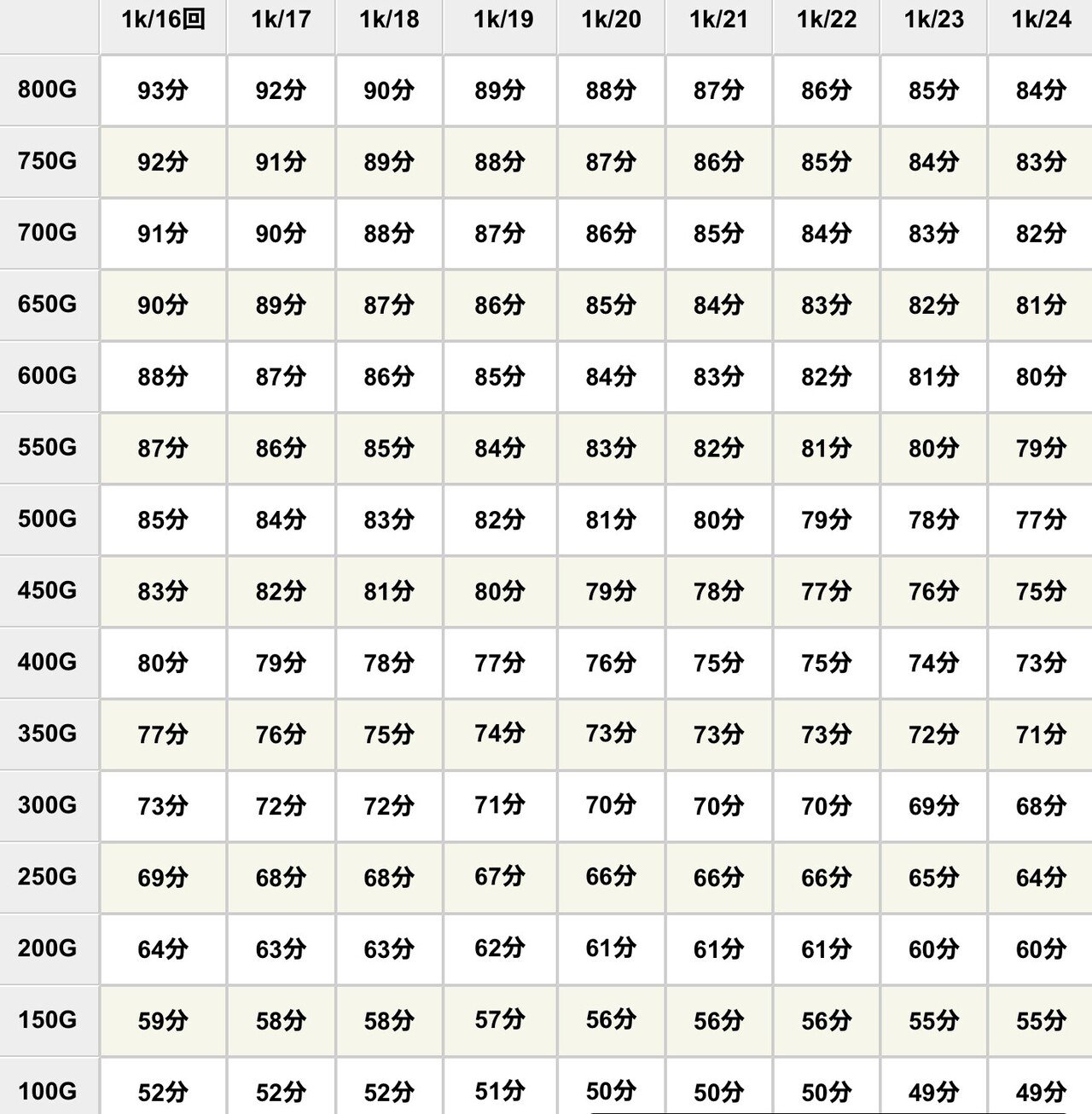
20回転=290回転とする。
そしてそこから±1回ごとに±5回転と仮定する。
（17回なら275回転・23回なら305回転）

ここからが閉店期待値です。

1k17.18.19.20回転の4種類を、出玉2パターンで計算してます。

上で挙げた平時の期待値からどの程度下がるのでしょうか？

1k/17回転①(143.5-△0.5-△0.7)

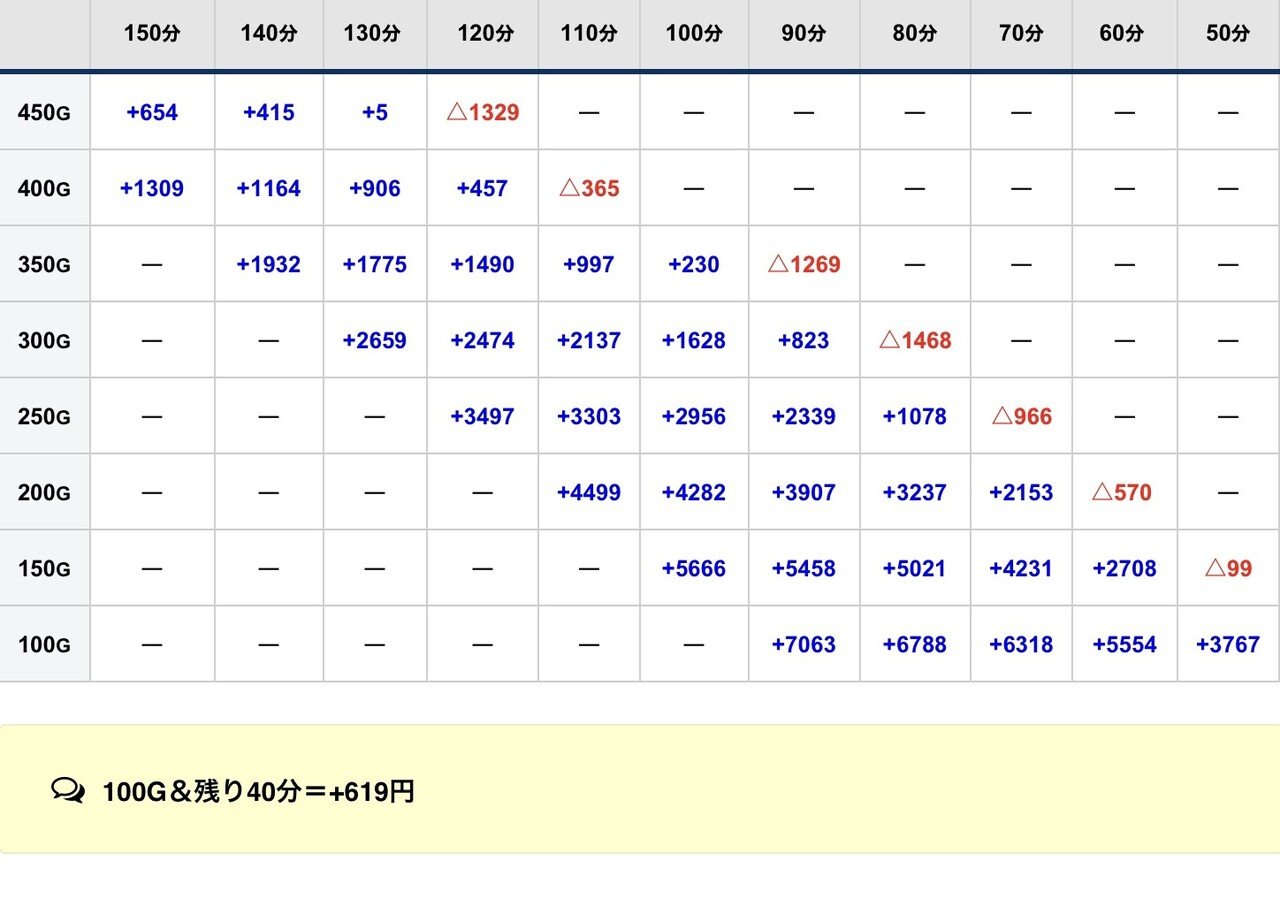
1k/17回転②(142-△0.75-△1.0)

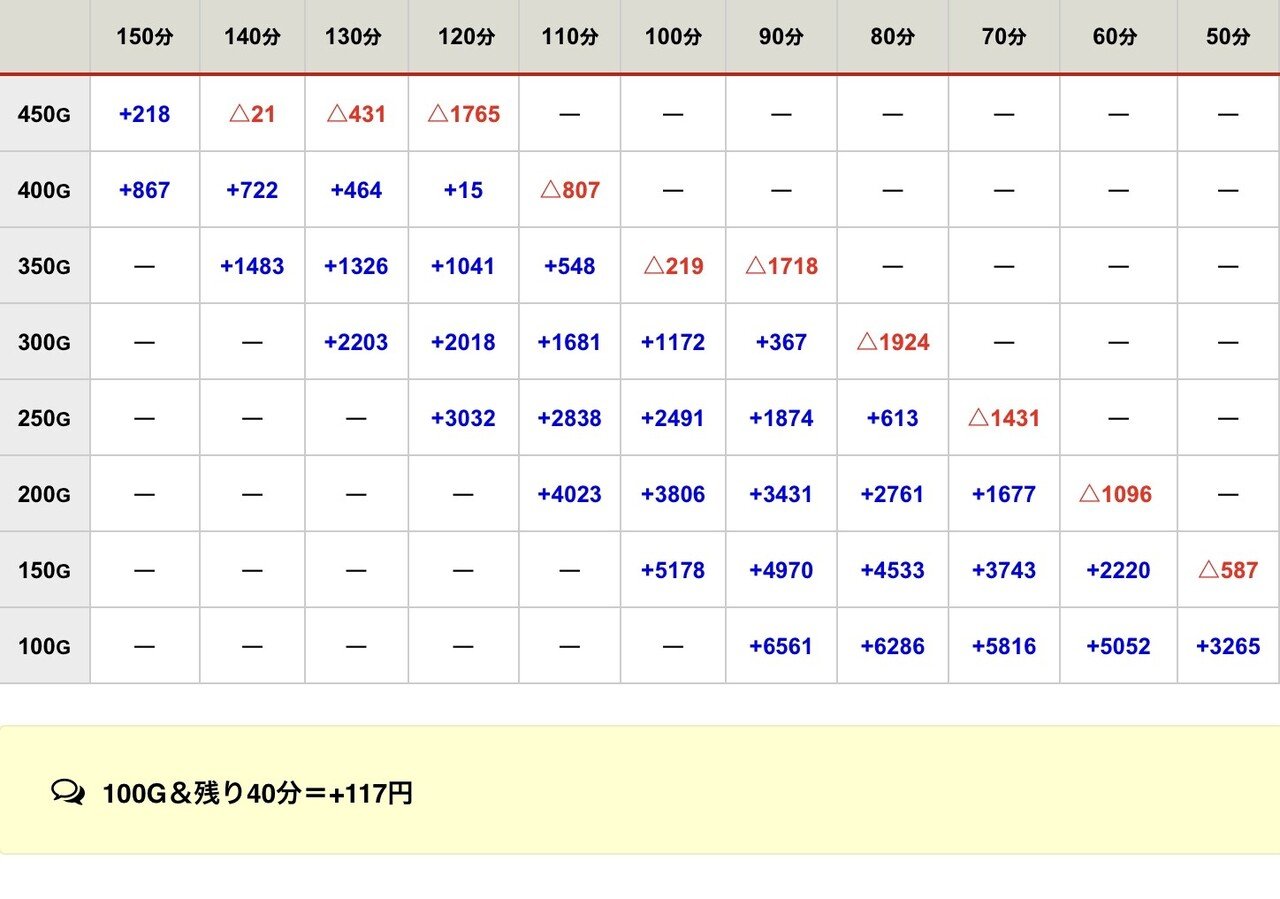
1k/18回転①(143.5-△0.5-△0.7)

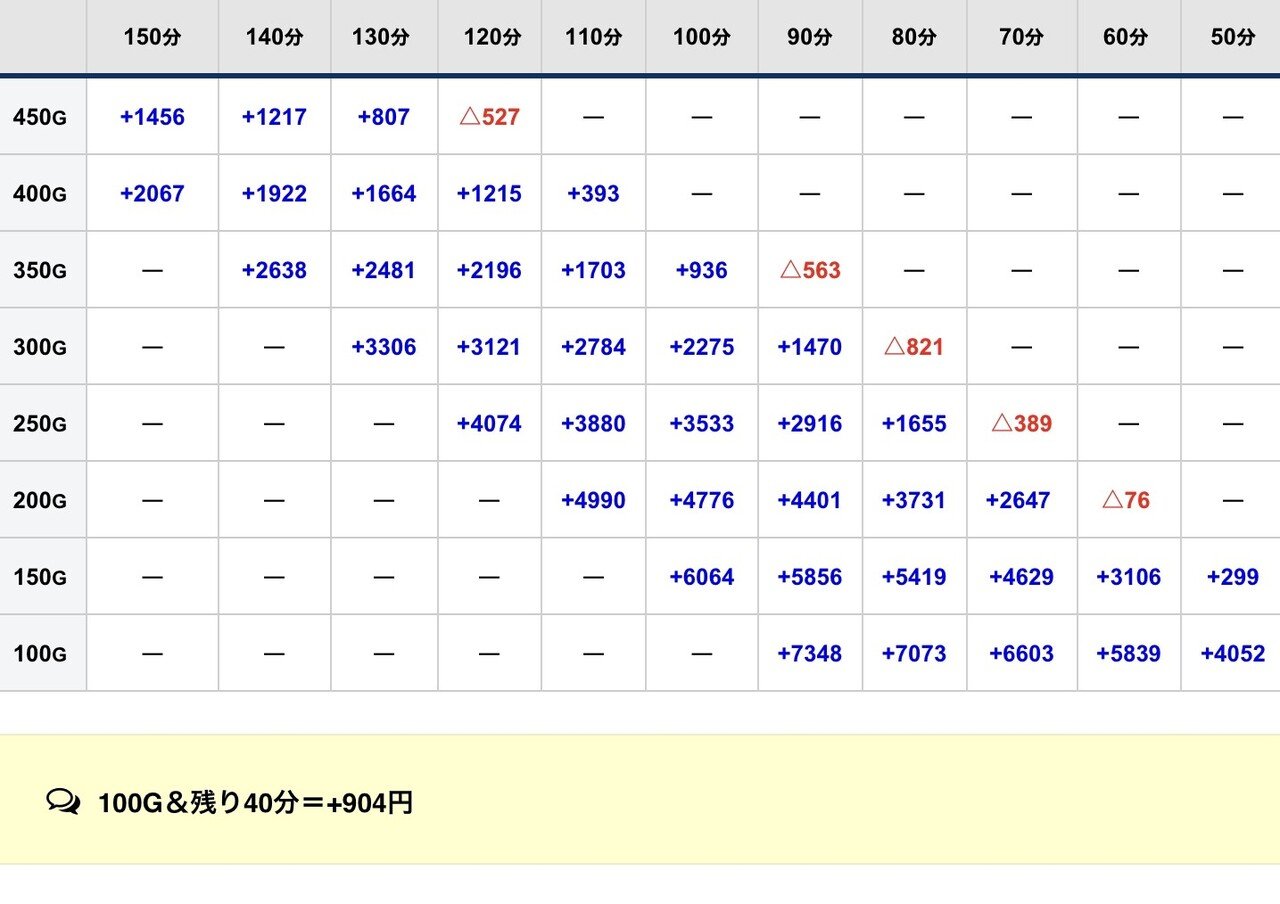
1k/18回転②(142-△0.75-△1.0)

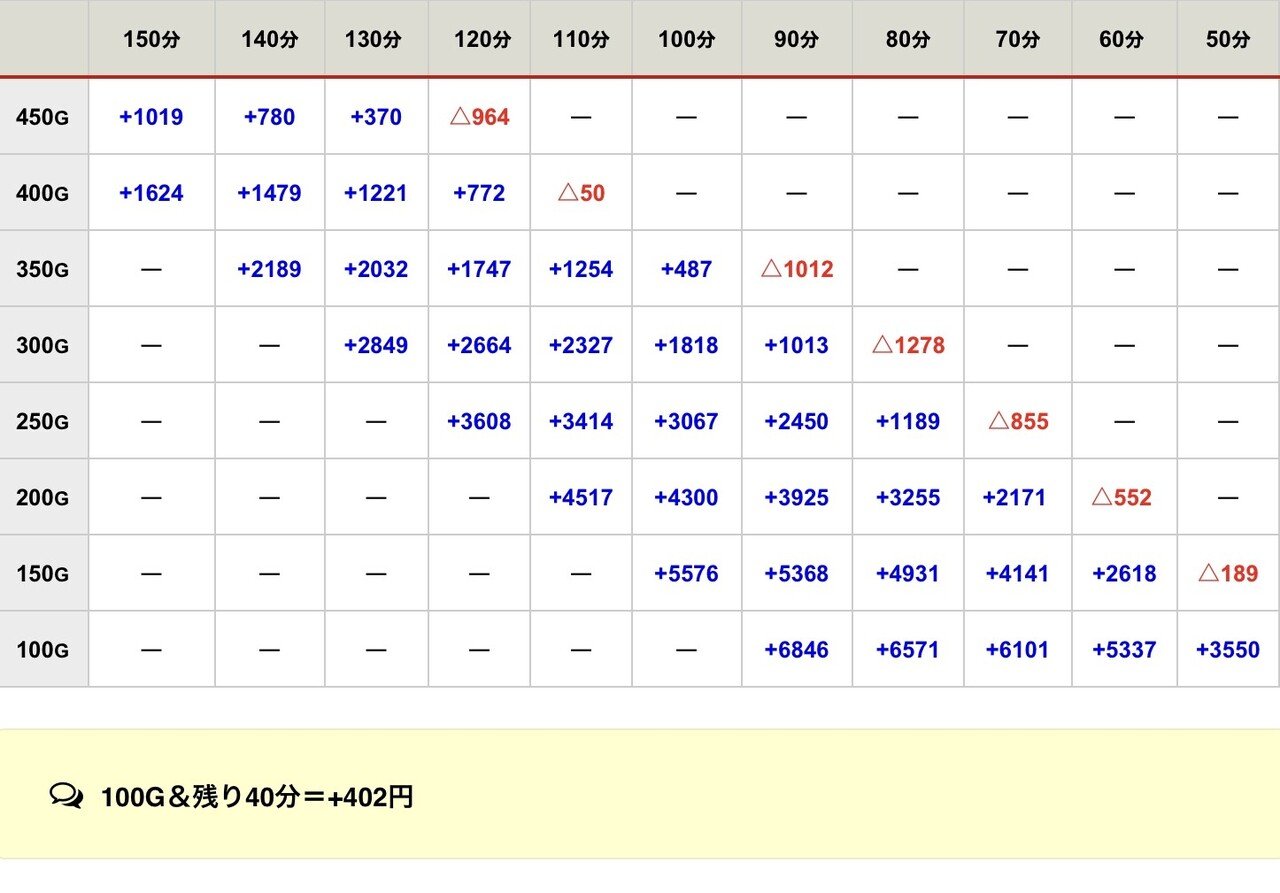
1k/19回転①(143.5-△0.5-△0.7)

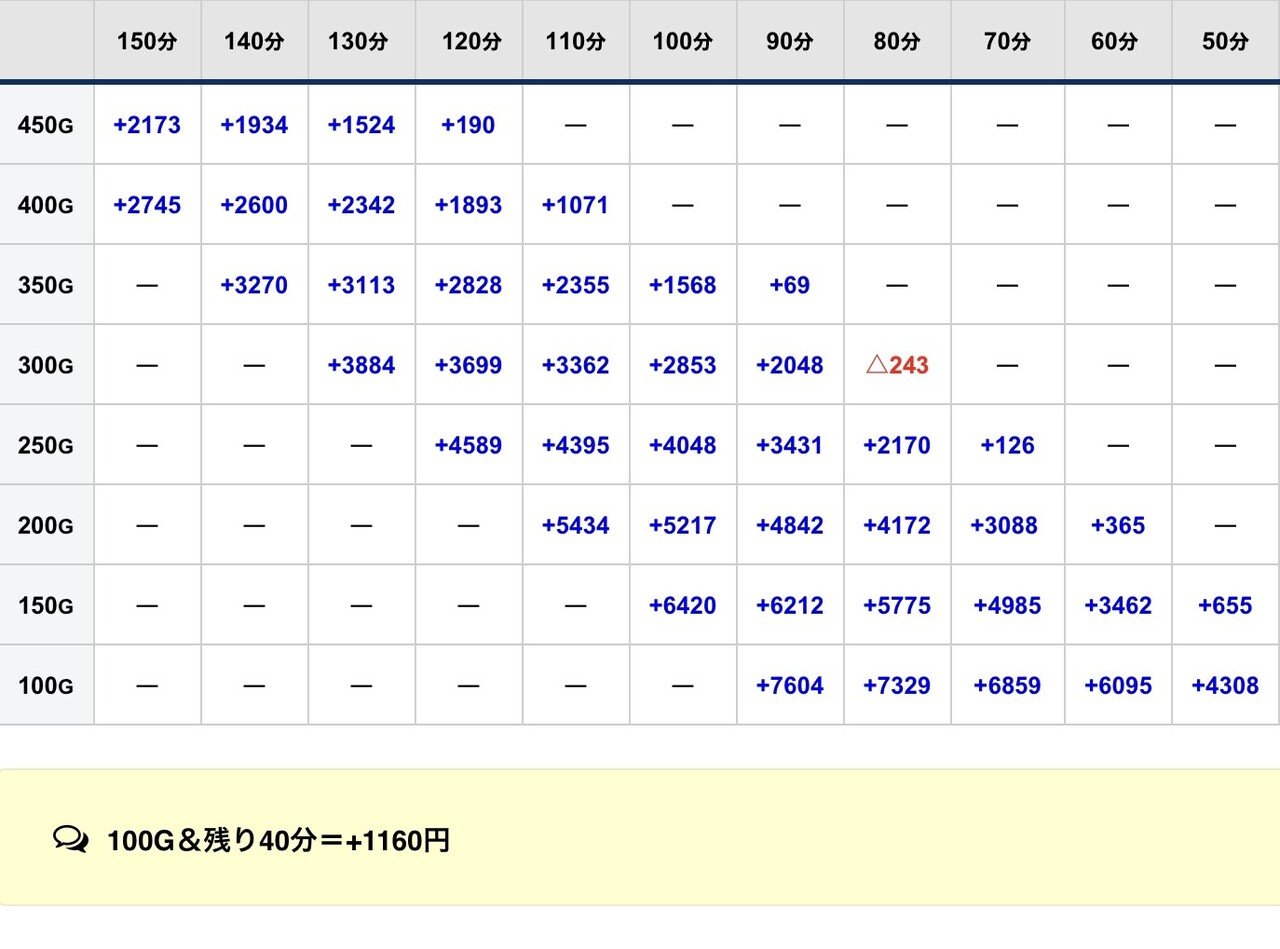
1k/19回転②(142-△0.75-△1.0)

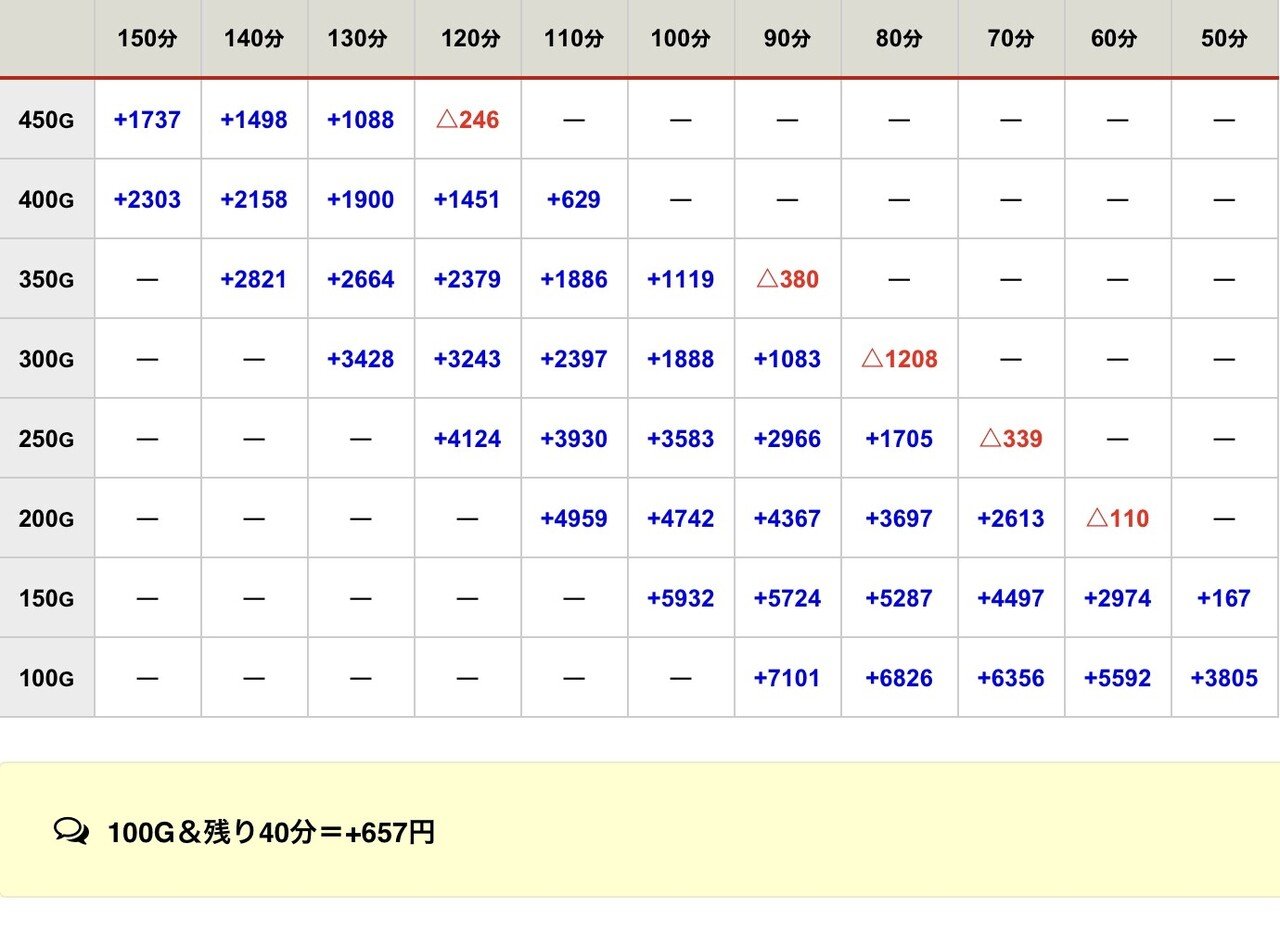
1k/20回転①(143.5-△0.5-△0.7)

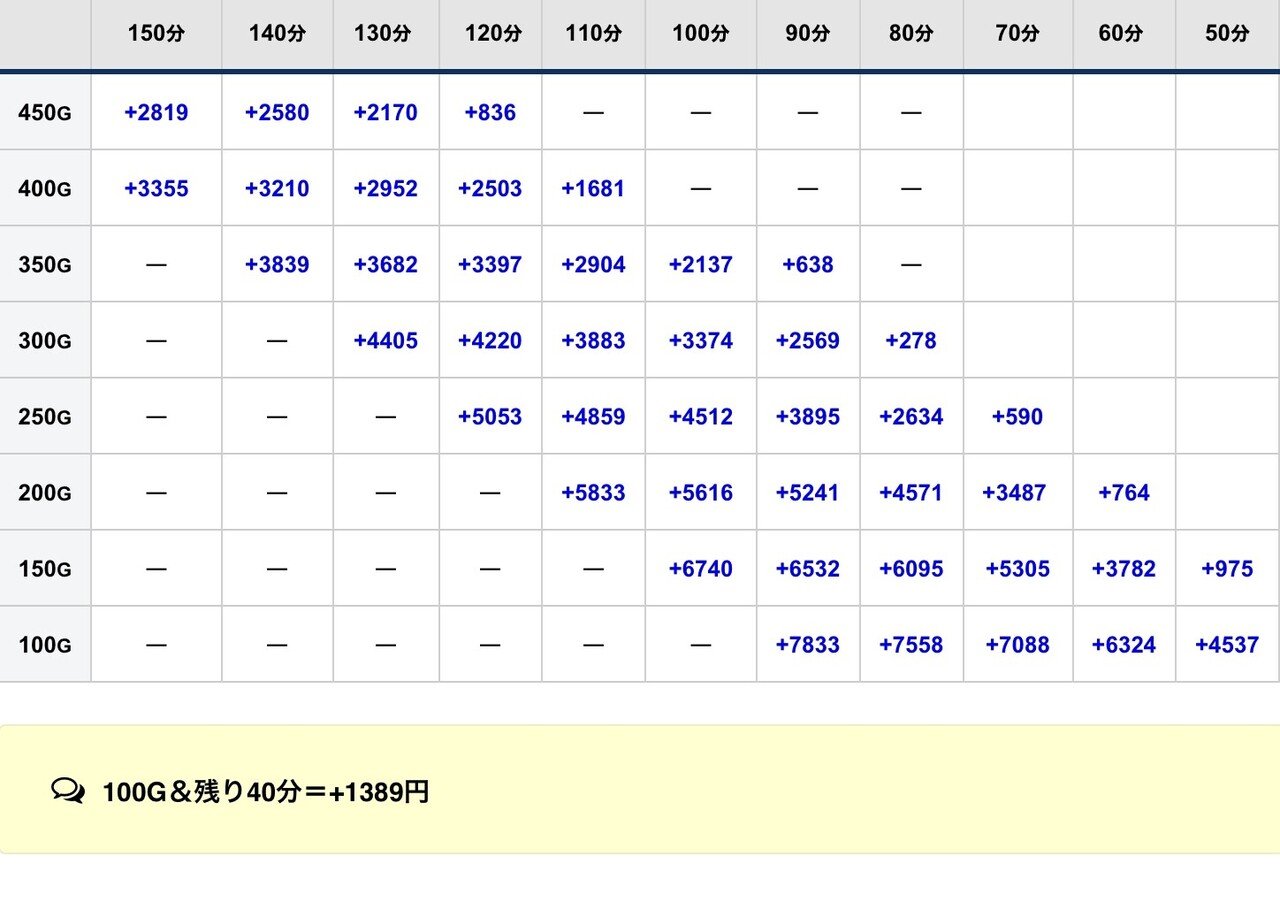
1k/20回転②(142-△0.75-△1.0)

.

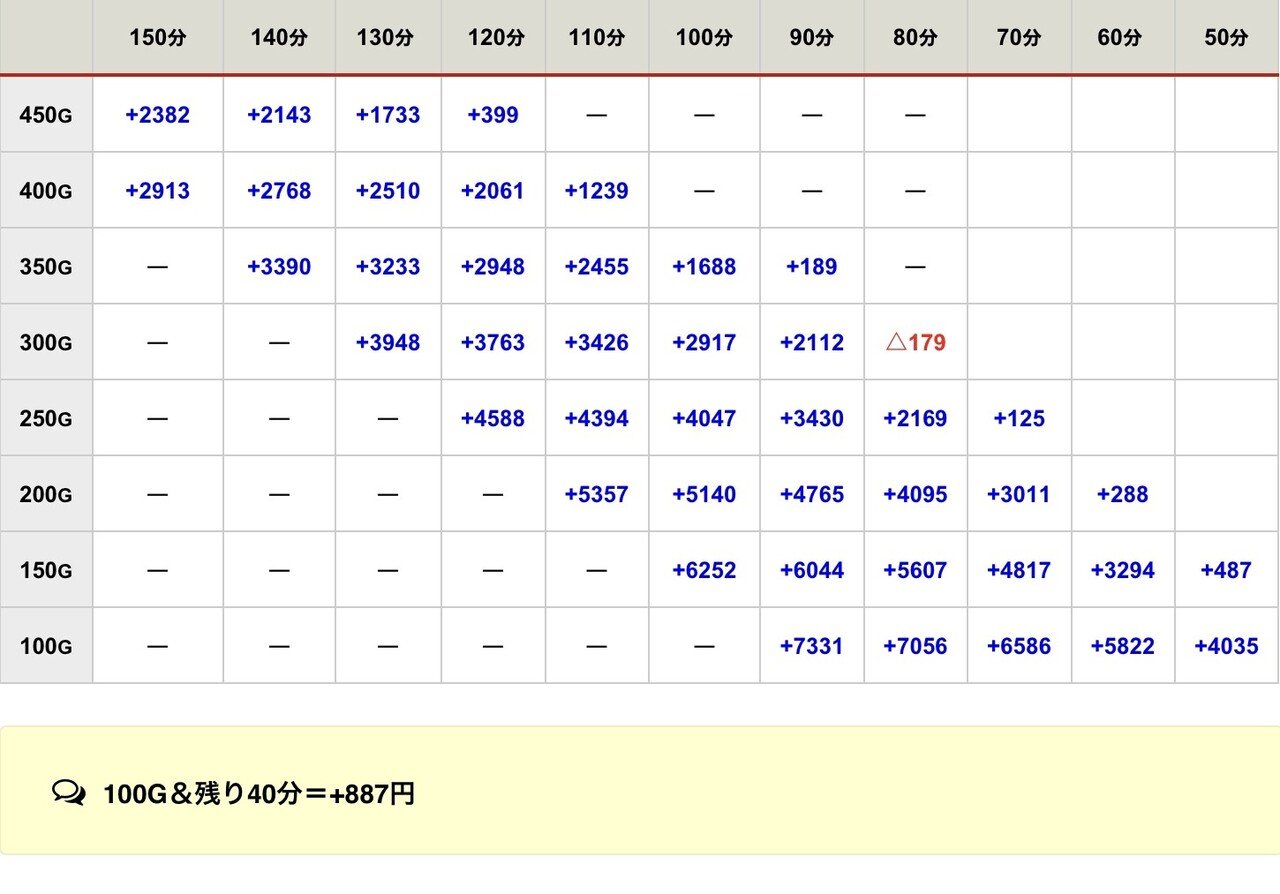
想像以上に遅い時間からでも行けますね！

僕も計算してみて初めて気づきました。

こうなると「過去に稼働して19.5～20.5回転(出玉も普通)が濃厚である台番」であれば残400G-残140分とかでも余裕で打てる、という結論になります。

逆に、知らない等価の店での残400G-残140分ならば打たないほうが良いでしょうね。。

まあ「何回転か？」「出玉は何玉か？」店の台番別で熟知していることが閉店稼働の前提となるでしょう。

.

シミュレート条件

143.5-△0.5-0.7
→
通常時の出玉 = 4204.48玉
遊タイム突入時の出玉 = 2726.14玉

142-△0.75-△1.0
→
通常時の出玉 = 4104.11玉
遊タイム突入時の出玉 = 2591.38玉

・閉店計算での通常時は1時間あたり275回転
・確変時短時は1分あたり12.5回転
・「確変or時短開始→大当たり→10R終了」のループ1回は6.8分
・1回目の大当たり消化は2.5分と仮定

実際の閉店稼働では、もう少し時間を短縮できるはずです。

19回や20回の台であれば1時間あたり290～305回転はイケるでしょうし、確変ループも1回当たり5.8～6.2分で済むでしょう。

.

具体的な閉店期待値の出し方①

そもそも閉店期待値をどうやって出しているのか？

「残300G-残100分」を例にして説明していきます。

当選までに要する時間は以下のように分布する。
→
5.5分後に当選 = 14.503%
16.4分後に当選 = 12.3998%
27.3分後に当選 = 10.6014%
38.2分後に当選 = 9.0638%
49.1分後に当選 = 7.7494%
60.0分後に当選 = 6.6254%
72.0分後に当選(遊タイム) = 16.6284%
86.3分後に当選(遊タイム) = 9.5489%
遊タイムスルー = 12.8797%

「10R終了→1G開始」の時点で以下の欠損が発生する。
→
残1分 = △2769.48玉
残2分 = △2579.88玉
残3分 = △2413.48玉
残4分 = △2277.45玉
残5分 = △2167.51玉
残6分 = △2050.78玉
※次回が確変か時短かは問わない

以上のような前提を置いております。

.

「残300G-残100分」。
初回大当たり(2.5分)が終了してからの残り時間は....

残92.0分 = 14.503%
残81.1分 = 12.3998%
残70.2分 = 10.6014%
残59.3分 = 9.0638%
残81.1分 = 7.7494%
残48.4分 = 6.6254%
残36.4分 = 16.6284%
残22.1分 = 9.5489%
遊タイムスルー = 12.8797%

欠損額が発生するパターンは計8種類あります。(残92.0～22.1の8種類)

この8種類を全て出していきます。

残22.1分 = 9.5489%の場合。
→
確変1ループが6.8分なので最高で+3.25連。
「+3.25連」→「3連終了して残1分に到達する」→「+3連した場合は△2769.48玉の欠損が出る」と置き換える。
+3連する確率は30.6939%（残保留4個を含む）。
30.6939%の確率で△2769.48玉の欠損が発生するということなので「残22.1分確変時短開始での欠損額は△3400.24円である」となります。

残81.1分 = 12.3998%の場合。
→
「最高で+11.93連」→「+11連終了して残6分に到達する」→「+11連した場合は2050.73玉の欠損」と置き換える。
+11連する確率は1.358%なので「残81.1分確変時短開始での欠損額は△111.40円である」となります。

残92.0分 = ？？？円×14.503%
残81.1分 = △111.40円×12.3998%
残70.2分 = ？？？円×10.6014%
残59.3分 = ？？？円×9.0638%
残81.1分 = ？？？円×7.7494%
残48.4分 = ？？？円×6.6254%
残36.4分 = ？？？円×16.6284%
残22.1分 = △3400.24円×9.5489%

.

残りの6種類を計算すれば「残300G-残100分」での閉店欠損を出せます。

答えを出してしまうと、8種の総和は△1246円です。

.

この1246円の欠損を回転数や出玉別に差し引けば、閉店期待値が完成します。

残300G・残100分
1k/20回転（1435-△0.5玉-遊△0.7玉）
→
平時4620-欠損1246=+3374円

残300G・残100分
1k/18回転（1420-△0.75玉-遊△1.0玉）
→平時3064-欠損1246=+1818円

ちなみに欠損額の一覧は以下のとおり。

1k/16や1k/21以上の場合は、下の欠損額を平時の期待値から差し引いてください。

.

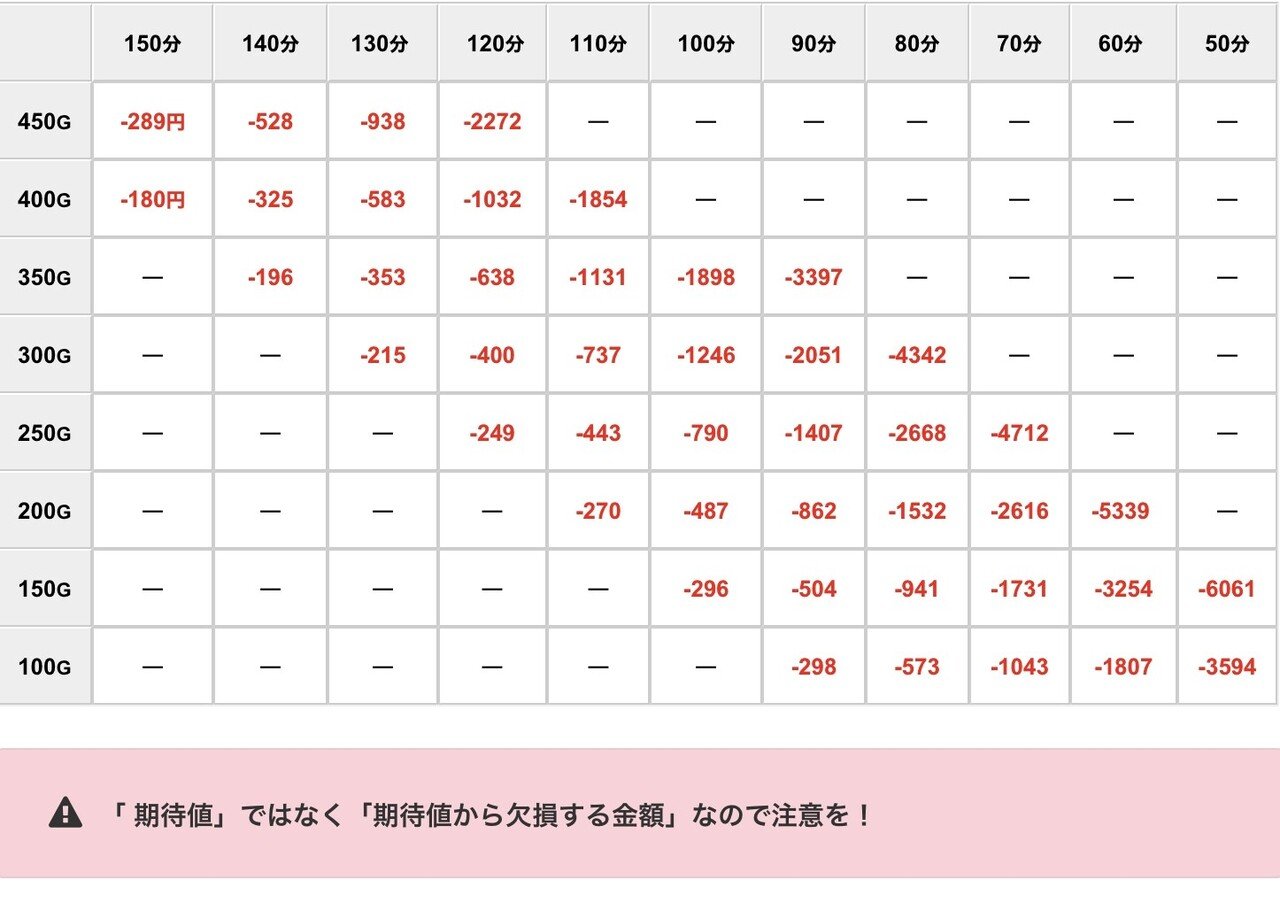
具体的な閉店期待値の出し方②

では「残100G-残40G」の場合はどうなるのか？

5.5分後に当選 = 14.503%
16.4分後に当選 = 12.3998%
22分後に遊タイム突入 = 73.0972%

残18分では遊タイムを225Gしか回せませんよね（分速12.5G）。

ここでは「遊タイムで当選する確率」と「残り遊タイム125+保留4Gを放棄する確率」を出す必要があります。

遊タイム225Gで当選する確率
＝50.5945%
ここでの欠損は「次回確変or時短の放棄」。

遊タイム225Gをスルーする確率
＝49.4055%
ここでの欠損は「残り遊タイム125G+保留4Gの放棄」。

まあ「次回確変or時短の放棄」の欠損計算は、「初回大当たりだけ消化して残1分用の欠損が出る」ということにしておきます。

すると「遊タイム225G以内に当選したら△2769.48玉が欠損する」ということになりますね。

.

次に遊タイム125+4Gの価値を金銭換換算します。

残り遊タイム125+4Gならば、
平均で106.28Gの遊タイムが得られる。
→
129G→106.28Gと減る理由としては、必ずしも129Gを消化できるわけではないから。
50Gで当たったら50Gの遊タイムしか得られないし、1Gで当たれば1Gの遊タイムしか得られないことになる。

遊タイム1Gの価値は+13.427玉。
「0.7玉投資すると1/319.6で4291.18玉が当選する」ということなので。
ちなみに遊タイム時は単発でも時短120Gなので、通常当選4204.48玉→遊当選4291.18玉になる。

遊タイム125+4Gを放棄すると△1397.98玉を欠損する。
106.28G×13.153玉=1427.02玉

5.5分後に当選 = 14.503%
16.4分後に当選 = 12.3998%
遊タイム突入 = 73.0972%
→
5.5分後に当選 = △217.39円
16.4分後に当選 = △408.47円
遊タイムで当選 = △4096.97円
遊タイム125+4G放棄 = △2061.42円

.

なので「残100G-残40分」の欠損額は△6784.25円である、となります。

.

.

では、ここらへんで。

なお海物語は非等価での遊タイム期待値も出してます。
換金レート5種×持ちメダル6種×回転数9種＝270パターンもの期待値が載っています。