2023年度第2回デジラボ:Kangaroo2を用いた応力の可視化
こんにちは。
北九州市立大学M2舟津、薮内、B4井原です。
今回はKerf-bendingを活用した構造物をGrasshopperでモデリングして、
kangaroo2で応力の可視化を行います。
Kerf-bendingとは板状の材料に切込みを入れて曲げ変形を積極的に活用することで自由な形を作る手法です。
Kerf-bendingを活用したベンチの制作を過去のデジラボでは行いました。
以下のリンクをご参照下さい。
https://note.com/digilab/n/nf0d4bb7dd214
過去のデジラボでのKerf-bendingは直線的な切欠きによって一方向へ曲げ変形するKerf-bendingのモデリングと切欠き量の最適化が行われていました。
そこで本デジラボでは"多次元に変形するKerf-bending"の可能性を探っていきたいと思います。
具体的には、以下に示すような自由な空間をKerf-bendingで実現することを目的として、このような形を実現するための効率的な切欠き方の追求を行っていきます。

目次
"Flexmaps"について
アルキメデスの螺旋のモデリング
アルキメデスの螺旋をKangaroo2で物理演算
"Flexmaps"について
まずは多次元への変形ができそうなKerf-bendingに関する先行研究の調査を行った結果、Kerf-bendingではありませんが、"Flexmaps"と呼ばれる、アルキメデスの螺旋の形に切り欠かれた板材を金物で組み合わせることによって自由な形を実現できる手法が示された論文を見つけました。
先行研究調査の結果、私たちは卍型の切欠き、アルキメデスの螺旋型の切欠きに着目しました。
そこでまずは、レーザーカッターでこれらの切欠き方をMDFに施して、どのような切欠き方であれば自由な形を作れそうか、実物を触ってみました
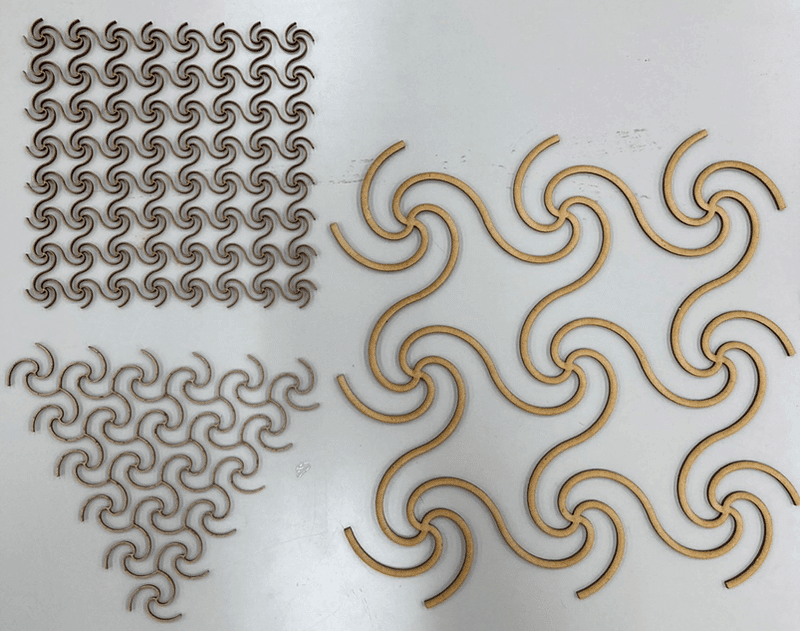
これらの切欠き方を検証した結果、アルキメデスの螺旋型の切欠きが非常に良く曲がりました。グニャグニャ曲がります。一方で卍型はかなり細かく卍を配置すれば曲がるものの、粗く配置すると全然曲がらない。
そこで狙った形をKerf-bendingで精度良く実現するには、アルキメデスの螺旋型が効率的な切欠き方ではないかと考えました。
アルキメデスの螺旋のモデリング
まずはGrasshopperのGHPythonを使って、アルキメデスの螺旋をモデリングしていきます。GrasshopperでGHPythonを用意して、入力と出力の端子を以下の写真のように設定してください。
アルキメデスの螺旋とは代数螺旋の一種であり、代数的な数式で表される螺旋です。
ここで、
"d"→"Type hint"→"int"
"s"→"Type hint"→"ghdoc Object when geometry"
"phi"→"Type hint"→"float"
"copy_count"→"Type hint"→"int"
とすることに注意してください。
なお、dは螺旋の分割数(細かくするほど曲線が滑らかになるが計算負荷増大)、sは螺旋の半径、phiは螺旋の巻き数、copy_countは螺旋の頂点の数(本稿では4で固定している)と設定しています。
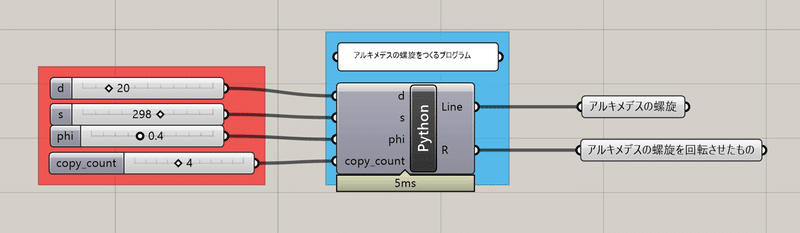
import Rhino.Geometry as rg
import math
#螺旋を構成する点を作成
points = []
for t in range(d+1):
t /= d # tを[0, 1]の範囲に正規化
r = 0.5 * s * (1 - t)
angle = t * phi * 2 * math.pi
x = r * math.cos(angle)
y = r * math.sin(angle)
z = 0
points.append(rg.Point3d(x, y, z))
# 螺旋を描画
spiral = rg.Polyline(points)
Line = spiral.ToNurbsCurve()
# 螺旋の始点を抽出する
angle = 0.0
x = r * math.cos(angle)
y = r * math.sin(angle)
z = 0.0
start_point = rg.Point3d(x, y, z)
# 回転のパラメータ
rotation_angle = 360/copy_count
rotation_axis = rg.Vector3d.ZAxis
# 曲線のコピーを格納するリスト
copied_curves = []
# 始点を中心に回転させる変換行列を作成
translation_vector = -start_point # 始点からの平行移動ベクトル
# 指定した回数だけ曲線をコピー
for i in range(copy_count):
# 回転行列の作成
rotation_angle_radians = math.radians(rotation_angle * i) # 回転角度をラジアンに変換
rotation_transform = rg.Transform.Rotation(rotation_angle_radians, rotation_axis, start_point)
# 曲線のコピー
copied_curve = Line.Duplicate()
copied_curve.Transform(rotation_transform)
# コピーをリストに追加
copied_curves.append(copied_curve)
# 結果を出力
R = copied_curvescopy

プログラムを組むと、上記のようなアルキメデスの螺旋が構築できると思います。
今回は上記のアルキメデスの螺旋をGrasshopperの"Kangaroo2"というコンポーネントを使って螺旋に生じる応力をパラメトリックに可視化し、なぜアルキメデスの螺旋の形に切り欠くと変形効率が良いか簡単に考察したいと思います。
"Kangaroo2"については過去のデジラボで紹介されています。以下のリンクをご参照下さい。Grasshopperにデフォルトで搭載されているコンポーネントですので、別途インストールの必要はありません。
https://note.com/digilab/n/n4cf007bca22b
アルキメデスの螺旋をKangaroo2で物理演算
物理演算の実行にあたってメインとなるコンポーネントは以下のsolverコンポーネントです。"GoalObject"を入力することで物理演算が実行されます。演算結果は点"V"やオブジェクト"O"へ出力されます。
Kangaroo2のコンポーネントについては以下のAppliCraftさんのサイトに詳しく記載されているため、そちらを見ていただくとよいと思います。
https://www.applicraft.com/ghcp_kangaroo2/
このコンポーネントを実行させるため、必要な解析条件として今回は以下に示す3つを挙げます。
・解析対象物の要素節点関係
・境界条件
・荷重条件
それでは上記4つの条件をひとつずつ設定していきます。

まずはモデリングしたアルキメデスの螺旋の要素節点関係を取り出します。
以下の3種類のコンポーネントを準備してください。
curve>Util>explode
curve>Analysis>PerpFrame(PFrame)
Kangaroo2>Goals_6dof>Beam
PerpFrameの"C"端は"Reparameterize"に変更してください。
以上のコンポーネントを以下のようにつなぎます。
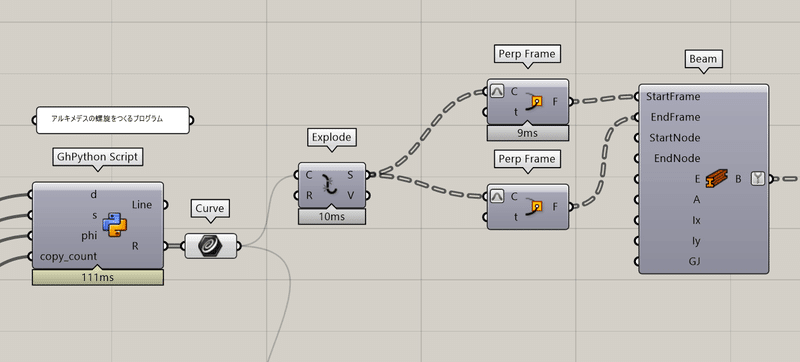
今回beamコンポーネントを使用したのは、曲げやねじれに抵抗を持つ梁要素としてのふるまうような条件を要素に与えるためです。
beamには要素の始点の平面と終点と平面をつなぐ必要があるため、
perpframeで要素の始点と終点の平面を取り出して、beamにつなぎます。
次にbeamに断面情報をつないでいきます。
幅をB、高さをH、ヤング係数をEとします。
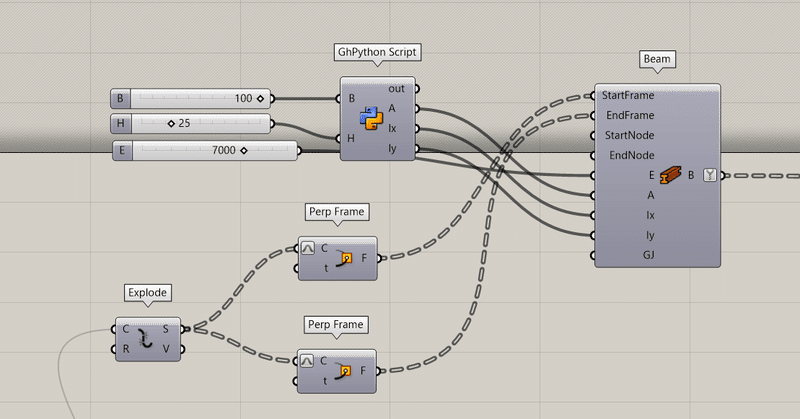
Beamには断面2次モーメントをつなぐ必要があり、GHpythonで以下のようなコードを入力します。
A=[]
lx=[]
ly=[]
A = BH
lx = (B*H**3)/12
ly = (H*B**3)/12次に境界条件の設定を行います。
kangaroo2で境界条件を入れるコンポーネントはanchorというコンポーネントとSupportというコンポーネントがありますが、今回は変位と回転を拘束できるSupportを使用します。
Supportを使用することで、ピン、ローラー、固定の設定が可能です。
4つのアルキメデスの螺旋の始点と終点をEndpointで出力し、境界条件を入力するpointを取り出します。
Supportには境界条件のFrameを入れる必要があるので、XYPlaneでpointの平面を作成し、それをSpportに入れます。
拘束はToggleで設定し、Falseだと自由、Trueだと固定となります。
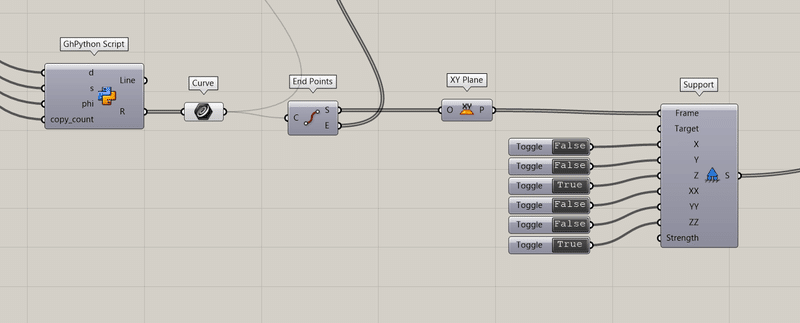
次に荷重条件の設定を行います。
今回は4つのアルキメデスの螺旋が繋がった中心に鉛直荷重をかけるので、
中心点をとりだします。
中心点は4つのアルキメデスの螺旋があるため、listitemで一つだけ取り出します。
それをLoadにつなぎ、方向と荷重の大きさを入れます。
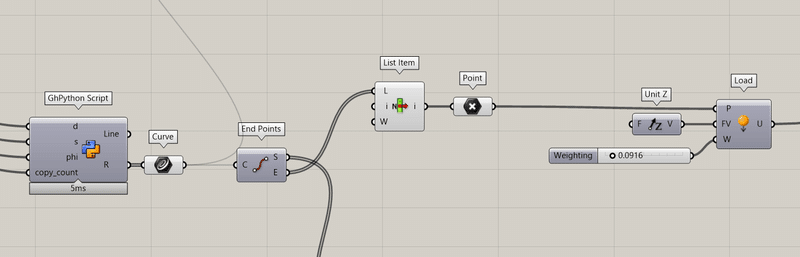
これで要素節点関係と境界条件、荷重条件の設定がおわったので、それらをEntwineにまとめます。
Entwineにまとめず、それぞれの条件をそのまま、solverにいれることもできますが、今回はc#でモーメントやねじりを可視化するときに、BeamのデータをExplode Treeで取り出す必要があるので、Entwineでそれぞれのデータをまとめています。
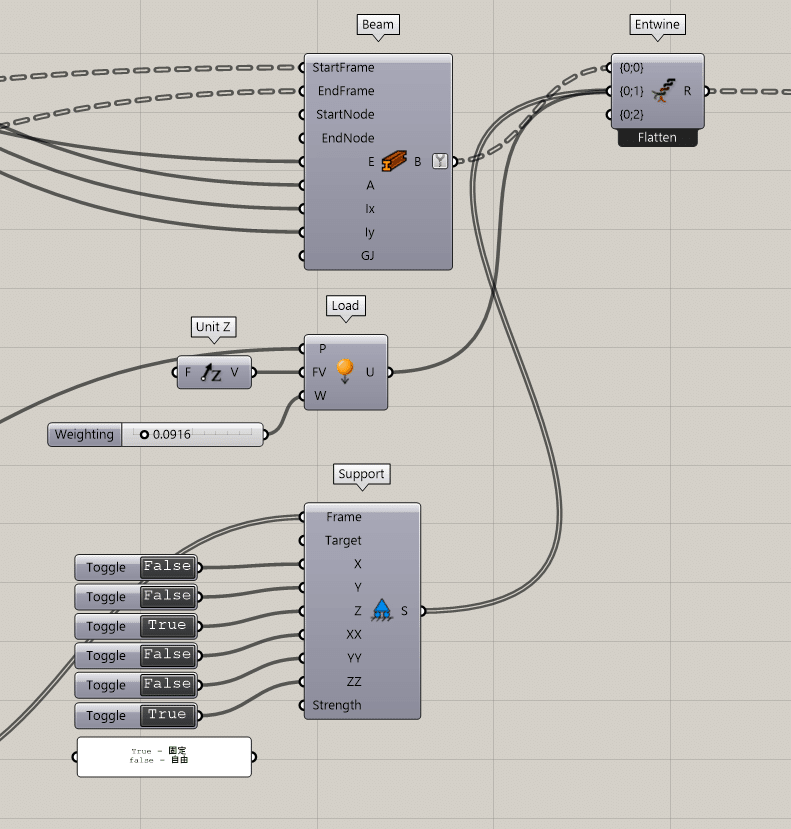
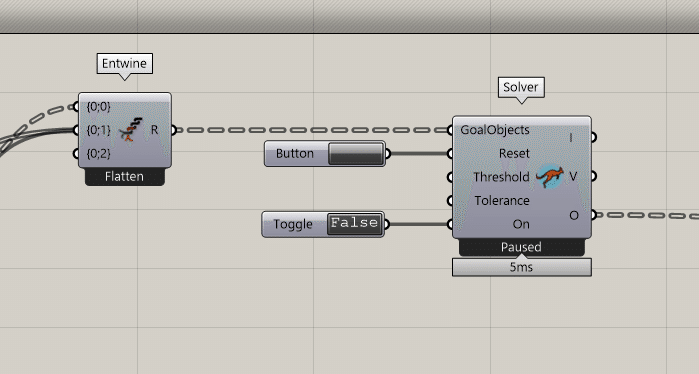
EntwineにまとめたデータをSolverに入力します。
ButtonをResetに、ToggleをOnにつなぎます。
ToggleがTrueの状態にすると、解析が行われ、Buttonを押すと解析が最初からとなります。
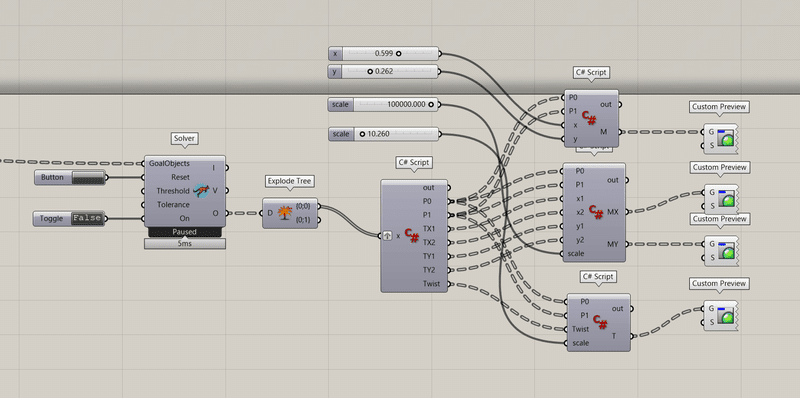
構造解析結果の可視化はC#で行います。
今回はKngaroo2のサンプルが公開されているDaniel Piker氏のGIthubを参考に作成しました。
New_for_241 > BeamExample1.gh
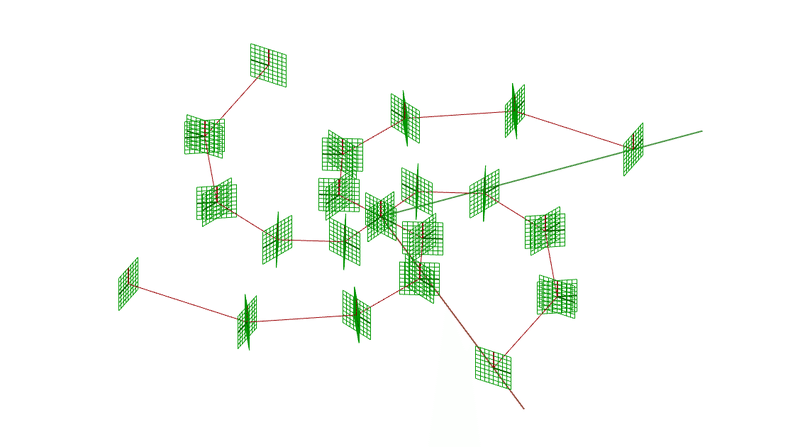
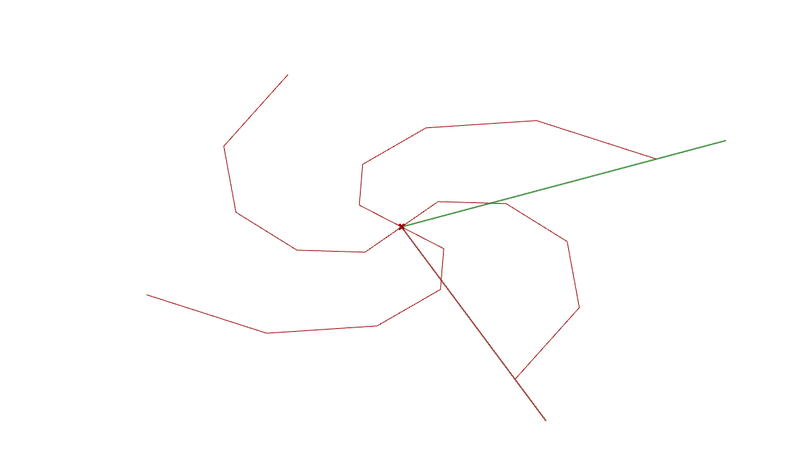
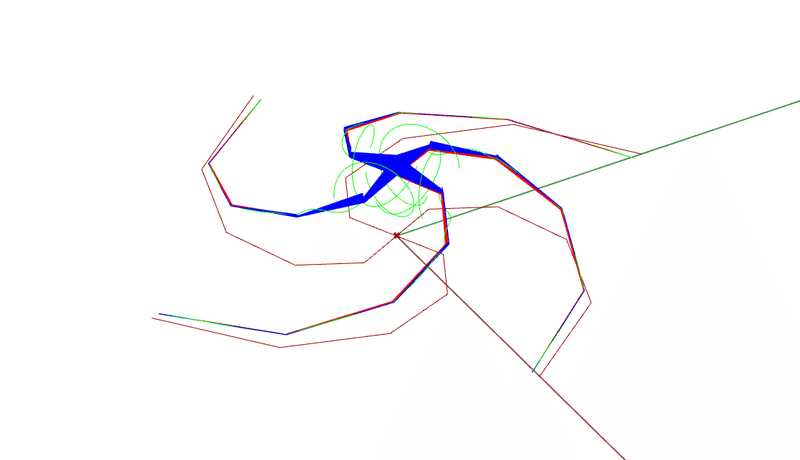
solverのtoggleをTrueにすると以下のような解析結果が表示されます。
参考URL
https://www.applicraft.com/tips/rhinoceros/kangaroo2/
New_for_241 > BeamExample1.gh
この記事が気に入ったらサポートをしてみませんか?
