
Concentrated Liquidity の理解 Part 1
Uniswap v3 や Orca の Whirlpool は集中流動性AMM (Concentrated Liquidity Automated Market Maker) です。
下記の Uniswap v3 の Whitepaper が原典となりますが、私自身は読んで難しく感じました。おそらく、私はもう少し図として何が起きているのかとらえたい人なのだと思います。
Whitepaper: https://uniswap.org/whitepaper-v3.pdf
Uniswap v3 の Whitepaper には $${\sqrt{P}}$$ や $${\sqrt{k} = L}$$ といった定義が出てきます。価格の平方根、Constant Product k の平方根、というそのものの意味はわかりますが、なぜそれが出てくるのかがわからず、唐突感がありました。
特に、なぜ $${\sqrt{P}}$$ なのかは、さっぱりわからなかったです。でも、実は Constant Product の AMM にもこの $${\sqrt{P}}$$ は潜んでいたことがわかりました。つまり、Constant Product の AMM と Concentrated Liquidity の AMM は別物ではなく、完全につながっています。
今回は、Concentrated Liquidity を理解する突破口になったと考えているグラフを記録に残します。
計算式が出てきますが、連立方程式を解いているぐらいで難しい変換はないと思います。
Constant Product の AMM
よくなされている説明と図
Constant Product の AMM のキモはたった 1 つの式で表されます。
$$
k = A_{amount} \cdot B_{amount}
$$
2 種類のトークン A と B の保有量の積がどの時点でも定数 $${k}$$ になるように保有量が調整される、それだけです。
この式は $${B_{amount} = \frac{k}{A_{amount}}}$$ の反比例の式ですので、下記のグラフの線上を移動することを意味します。

このグラフにおいて、トークン A をトークン B にスワップすることはグラフ上の $${(A_1, B_1)}$$ から $${(A_2, B_2)}$$ への移動を意味します。

トークン A の入力量を $${A_{input}}$$ とした場合、下記の関係式からトークン B の出力量である $${B_{output}}$$ が一意に決まります。
$$
k = A_1 \cdot B_1 = A_2 \cdot B_2 = (A_1 + A_{input}) \cdot (B_1 - B_{output})
$$
そして、この図で価格 $${P}$$ は次の式で表されます。保有している2種類のトークンの保有量の比率が価格となっているのです。
$$
P = \frac{B_{amount}}{A_{amount}}
$$
先程のスワップの図においては、$${(A_1, B_1)}$$ 地点での価格は $${P_1 = \frac{B_1}{A_1}}$$ であり、 $${(A_2, B_2)}$$ 時点での価格は $${P_2 = \frac{B_2}{A_2}}$$ となります。
計算の順番の逆転
さて、これまでの計算の順番を振り返ってみると、$${A_{amount}}$$ と $${B_{amount}}$$ が決まることにより、定数 $${k}$$ や、ある地点における価格 $${P}$$ が決まるという流れでした。
ここで、これを逆転させます。つまり、定数 $${k}$$ と変数である価格 $${P}$$ が決まれば、グラフ上のある地点が特定でき、$${A_{amount}}$$ と $${B_{amount}}$$ が決まるという順番にします。
下記の 2 つの関係を使い、$${A_{amount}}$$ と $${B_{amount}}$$ の計算式を作ります。
$$
\begin{array}{ccl}
k &=& A_{amount} \cdot B_{amount}\\\ \\\
P &=& \frac{B_{amount}}{A_{amount}}
\end{array}
$$
まず、$${A_{amount}}$$ です。
$$
\begin{array}{ccl}
P &=& \frac{B_{amount}}{A_{amount}}\\\ \\\
&=& \frac{\frac{k}{A_{amount}}}{A_{amount}}\\\ \\\
&=& \frac{k}{A_{amount}^2}\\\ \\\
A_{amount}^2 &=& \frac{k}{P}\\\ \\\
A_{amount} &=& \sqrt{\frac{k}{P}}\\\ \\\
&=& \frac{\sqrt{k}}{\sqrt{P}}\\\
\end{array}
$$
次いで、$${B_{amount}}$$ です。
$$
\begin{array}{ccl}
P &=& \frac{B_{amount}}{A_{amount}}\\\ \\\
&=& \frac{B_{amount}}{\frac{k}{B_{amount}}}\\\ \\\
&=& \frac{B_{amount}^2}{k}\\\ \\\
B_{amount}^2 &=& k \cdot P\\\ \\\
B_{amount} &=& \sqrt{k \cdot P}\\\ \\\
&=& \sqrt{k} \cdot \sqrt{P}\\\
\end{array}
$$
これで下記の計算式が得られました。
$$
\begin{array}{ccl}
A_{amount} &=& \frac{\sqrt{k}}{\sqrt{P}}\\\ \\\
B_{amount} &=& \sqrt{k} \cdot \sqrt{P}\\\
\end{array}
$$
念のためもともとの関係式を満たしているか確認しておきます。
$$
\begin{array}{}
k &=& A_{amount} \cdot B_{amount} &=& \frac{\sqrt{k}}{\sqrt{P}} \cdot (\sqrt{k} \cdot \sqrt{P}) &=& \sqrt{k}^2 &=& k\\\ \\\
P &=& \frac{B_{amount}}{A_{amount}} &=& \frac{\sqrt{k} \cdot \sqrt{P}}{\frac{\sqrt{k}}{\sqrt{P}}} &=& \sqrt{P}^2 &=& P
\end{array}
$$
ここで驚いたことが2つありました。
1つ目は計算の中で $${A_{amount}^2}$$ や $${B_{amount}^2}$$ が出てきて、平方根を取る流れで、$${\sqrt{P}}$$ や $${\sqrt{k}}$$ が自然に登場してきたことです。
2つ目は $${k}$$ が定数であるため、$${\sqrt{k}}$$ もまた定数であり、いまや $${A_{amount}}$$ と $${B_{amount}}$$ は $${\sqrt{P}}$$ の反比例と比例の式になってしまったことです。
価格を軸にしたグラフ
さて、$${A_{amount}}$$ と $${B_{amount}}$$ が $${\sqrt{P}}$$ の反比例と比例の式になったため、これをグラフにしてみます。
なお、$${\sqrt{k}}$$ は定数であるため、$${L}$$と表記していきます。
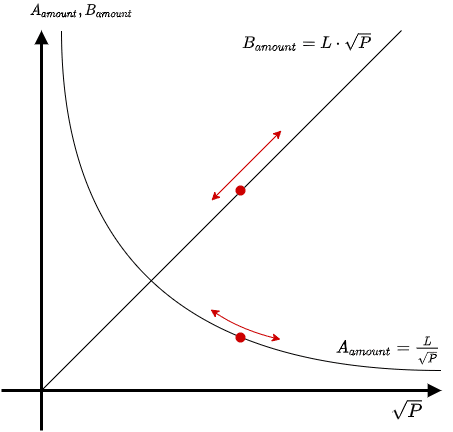
横軸は $${\sqrt{P}}$$ であり、縦軸はトークン A と B の保有量になります。
さて、スワップはどうなるでしょうか。

このグラフにおいて、トークン A をトークン B にスワップすることはグラフ上の $${(\sqrt{P}_1, A_1)}$$ から $${(\sqrt{P}_2, A_2)}$$ への移動と、 $${(\sqrt{P}_1, B_1)}$$ から $${(\sqrt{P}_2, B_2)}$$ への移動を意味します。
トークン A の入力量を $${A_{input}}$$ とすると、$${A_2}$$ と $${\sqrt{P}_2}$$ が求まり、$${B_2}$$ および $${B_{output}}$$ が決定します。
L が増加することのグラフ上の意味
Concentrated Liquidity に話を進める Part 2 で決定的な意味を持ってくるのが $${L}$$ です。これはもともと $${k}$$ が定数であるため、$${\sqrt{k}}$$ も定数だから、$${L = \sqrt{k}}$$ として表記するために導入しました。
なぜ $${L}$$ なのかといえば、そうです、これが Liquidity を表現する数値だから L が選ばれています。
$${L}$$ が Liquidity だということの納得感はなくて大丈夫です。ここでは単に $${L}$$ の数字が大きくなるとグラフ上でどんな変化が起きるのかを確認します。

$${A_{amount}}$$ も $${B_{amount}}$$ もどちらも $${L}$$ には比例する数式のため、$${L}$$ が 2 倍になると、グラフも各地点で 2 倍の値を取ります。
$${\sqrt{P}}$$ の変化に対する $${A_{amount}}$$ と $${B_{amount}}$$ の変化も 2 倍になるため、$${\sqrt{P}}$$を同じ幅動かすのに 2 倍のトークン量を投入する必要があります。逆に言えば、同じトークン量のスワップに対して、価格変動を起こしにくくなったということです。

まとめ
2種類のトークンの保有量を y 軸と x 軸に使用するグラフではなく、価格($${\sqrt{P}}$$)を x 軸に使用するグラフを描きました。
そのグラフにおいて2種類のトークンの保有量は $${L = \sqrt{k}}$$ とすることで下記の2式で表現されました。
$$
\begin{array}{ccl}
A_{amount} &=& \frac{L}{\sqrt{P}}\\\ \\\
B_{amount} &=& L \cdot \sqrt{P}\\\
\end{array}
$$
Uniswap v3 の Whitepaper に登場した $${L}$$ や $${\sqrt{P}}$$ は Concentrated Liquidity 固有の考えではなく、Constant Product の AMM にも使える考え方であることがわかりました。
Part 2 ではこのグラフに Concentrated Liquidity AMM ではどうなるのかを一目瞭然になるように追記していきます。
この記事が気に入ったらサポートをしてみませんか?
