
記号論理学とは...?(記号論理の基本事項をまとめた記事) (AMC 2023 Day9)
皆さんこんにちは!cipherです!この記事は仮の人さん主催の ”AMC2023 (Advent Math Calendar2023)”の記事になっています。
(初めてこういう記事を書くので至らぬ点もたくさんあると思いますが、どうか温かい目で見てほしいです。)1~8日目の方々の出来がすごくて横転してます。まだ見ていない方はぜひ見に行ってみてください!
九日目に私が取り扱う内容は記号論理学です。(私のTwitter(X)プロフィールを見たことがある方は、『記号論理学』という名前だけは知っているのではないでしょうか?)AMCでは自分の好きなことを発表できる場でもあるので今日、競技数学erには、記号論理学はどういう事をしている学問なのかを説明していきたいと思ってます。基本的に記号論理の入門書である前原記号論理の流れと同じような感じで記事は進めていきます。(基本部分をまとめた感じです)
(すでに前原記号論理を読まれている方は、ほぼ同じ内容なので復習がてらに読んでみてください。)
記号論理学とは…
記号論理学とは数学的な論理の構造や性質に焦点を当て、論理記号を用いて単純な命題を結びつけて複雑な命題を表し、その妥当性を明らかにしていき、思考の道筋を真理(真か偽)という概念を用いて説明する学問です。

https://www.youtube.com/watch?v=oF6B-HOKvHAより
T,Fは真理値であり、その命題が真(True)か偽(False)であるかを示す
1,命題の表現法
前提知識
記号論理学に入る前にこの記事で使う用語について説明します。(流派などがあり、異なることが多いので注意)
1、論理記号、用語
→ ………………… ならば
⇄ ……………….. 同値である
∧ ………………. and
∨ ……….……….. or
¬ ………………… not
∀ ………………… すべて(全称量化)
∃ ………………… 存在する(存在量化)
∃! ………………….ただ一つ存在する(唯一存在量化)
まず、この章ではこれらを用いて命題をどのように表現するのかを軽ーく説明します。
1 命題結合記号
命題A、Bが与えられた時、$${¬A}$$とか$${A→B}$$という記法により次のような命題を表します。
$${A→B}$$…………….AならばB
$${A⇄B}$$…………….AとBは同値
$${A∧B}$$……………..Aであり、さらにBでもある
$${A∨B}$$……………..AまたはB
$${¬A}$$……………….Aではない
2 命題と命題関数
命題とは真or偽が定まる性質をもつものです、この性質を真理値を持つといいます。命題関数とは変数を含む命題、つまり関数値が命題であるような関数を表すものを考えます。たとえば
$${4x+2y=10}$$ という命題を$${F(x,y)}$$と表せばFは
$${F(1,3)}$$なら10=10という真な命題
$${F(2,0)}$$なら8=10 という偽な命題
となるような一つの関数を表していると考えられます。
つまりF(x)に任意の値aとかbとかcとかを代入したらF(a)は真、F(b)は偽、F(c)は偽となるのが命題関数です。
3 全称量化と存在量化
1変数xの命題関数F(x)が与えられた時、 ∀xF(x)および∃xF(x)はそれぞれ
$${∀xF(x)}$$……………….すべてのxに対して$${F(x)}$$
$${∃xF(x)}$$………………$${F(x)}$$というxが存在する
となります。
4 論理記号の用例①
4.1 必要条件 十分条件 必要十分条件
FとGとを任意に与えられた述語( $${F()}$$←これの事 <…はFである>と読む)として すべてのxにおいて<xはFならばxはG> という命題を論理記号を用いて表すと
$${∀x(F(x)→G(x))}$$ となります
FとGを<条件>と見たときこの命題を<FはGであるための十分条件>とか
<GはFのための必要条件>と読みます。
またFとGを<集合>で考えるとき($${F(x)}$$や$${G(x)}$$の代わりに$${x∈F、x∈G}$$とします)上記の命題は
$${∀x(x∈F→x∈G)}$$
となります。
この命題をは $${F⊂G}$$ という記号で表し、<FはGの部分集合>と読むのです。
4.1.2 次に $${∀x(F(x)⇄G(x))}$$ という命題に考えてみましょう。
先ほどと同様に、FとGを条件とみなすと<FはGのための必要十分条件>とか<GはFのための必要十分条件>と読みます。またFとGを集合で表すとこの命題は $${∀x(x∈F⇄x∈G)}$$
と表されて、これを簡単に
$${F=G}$$ と書きます。
4.2.1 和集合 積集合 余集合
<FまたはG>という命題を考える場合それらは<すべてはFかGである>という事なのですなわち、
$${∀x(F(x)∨G(x))}$$
という事であります。
<FまたはG>を述語と考える場合には、それが<…FまたはGである>という述語の事でありそれは
$${F(x)∨G(x)}$$
をxの関数(命題関数)と考えそれをH(x)と表したときの$${H()}$$の事です。
補足、<FまたはG>と<…はFまたは…はGである>と$${H()}$$は同じ意味
4,2,2 F,G,Hを全ての集合と考える場合には上のような集合Hの事を
FとGとの和集合と呼び$${F∪G}$$ という記号で表します。
H(x)はF(x)∨G(x)そのものなのでしたがって
$${∀x[H(x)⇄(F(x)∨G(x))]}$$
という命題は成立します。すなわちこれは正しい命題であり$${F∪G}$$の定義を表す命題です。
4,2,3 F,Gという述語<Fであり、またGであるという>というとき
それを $${∀x(F(x)∧G(x))}$$
という命題を考える場合と
$${F(x)∧G(x)}$$
という命題を考えるときがあります。
$${F(x)∧G(x)}$$という命題関数$${H(x)}$$と表すときこのF,G,Hを全て集合ととらえるならば、このHをFとGの積集合(共通部分)といい$${F∩G}$$ という記号で表します。したがって$${∀x[H(x)⇄(F(x)∧G(x))]}$$ という命題は正しい命題でありF∩Gの定義を表す命題です。
4.2,4<Fではない>というものに関しても同様です、Fを述語にしたとき
$${∀x¬F(x)}$$
という命題と考えられる場合もあれば
$${¬F(x)}$$
という命題関数と考えられる場合もあります。
この¬Fという述語を集合として考えるとこの¬FはFの補集合や余集合と言いしばしば $${F^c}$$
などという表記で表されます。これに関して
$${∀x(x∈F^c⇄¬(x∈F))}$$
という、命題が成立します。
5,論理記号の用法② 素数が無限にあることの表現
5,1 =、+という記号を用いれば a<b という命題は
$${∃x(a+x=b)}$$
と表せられます。
また<bはaで割り切れる>ということを
$${a|b}$$
と表します、これは
$${∃x(ax=b)}$$
という事です。
5,2 <1と自分自身以外に約数を持たない数>を素数とすると<aは素数である>という命題は
$${∀x[x|a→(x=1)∨(x=a)]}$$
という事です、また1は素数ではないので<aは素数である>の本当の定義は
$${∀x[x|a→(x=1)∨(x=a)]∧¬(a=1)}$$
ということになります。
5,3,1 素数は無限に存在する、これはユークリッドやオイラーによって証明された有名事実ですがこれを論理記号を用いてどのように表すでしょうか?
勿論述語であるF()を<….は無限にある>とすれば終わってしまいますがこれ自体にはあまり意味はありません、これでは定理の意味をはっきりさせるのに何の役にも立ちません。なので次に<….は無限にある>という述語を定義しようと思います、しかし自然数に絞っておくならば、例えばユークリッドの素数の定理は
∀x∃y(x<y∧Prim y)
(Primは<…は素数である>という述語)
訳 すべてのxにおいて,より大きい素数であるyが存在する
と表せられます、Primの部分を省略せずに書くと
∀x∃y(x<y∧([y|a→(y=1)∨(y=a)]∧¬(y=1))
となります。
5,3,2 補足、一般に,自然数を元とする集合Fが無限集合であるという事は
∀x∃y(x<y∧y∈F)
と表されます。
変数を自然数に限定しない任意の集合を考えると
∀x∃y(x<y∧y∈F)
という命題は<Fが無限集合>を表しているのではなく集合Fには上に有界ではない>ということを意味しています。
例えば実数全体で考えると区間
{x|0<x<1}
は上に有界だけれど無限集合です。自然数だけを対象として考える場合には<上に有界でない集合>というのがちょうど<無限集合>というものと一致します、例えば<ユークリッドの定理>を上記のようにあらわすことが出来たのです。
自然数に関する任意の述語Fに関して
∀x∃y(x<y∧F(y))
という命題をG(F)と表すことにすればこのG()が<…は無限にある>ということを表すことになります。これは<自然数に関する述語>ではなく、<述語の述語>つまり<性質の性質>であります。<…は無限にある>という述語は<述語の述語>すなわち第2階の述語の意味に解していたという事です。
つまり、ここで何が言いたかったかというとユークリッドの素数の定理である<素数は無限にある>というのは、根源まで戻ると実は
∀x∃y(x<y∧([y|a→(y=1)∨(y=a)]∧¬(y=1))
という=、+、×や自然数を代表するいくつかの変数と論理記号で表現することが出来る。です
2,演繹
記号論理学の基本用語や論理記号の使用例を見てきましたが、ここからは演繹(えんえき)論理という、ある一般的な規則に従って仮定と前提から様々な結論を導く論理というものをやっていきます。
1,→について
演繹的推論の説明の第一として
$${A→B}$$
という命題があったときに、これはAという仮定からBが導き出されるつまり命題AからBが演繹される、ということを意味します、つまり
AとA→Bという二つの前提からBという結論を導いてもよいでしょう。
このような推論をしばしば

のようにあらわします。このように推論を図式で表したものを推論図と言います。この時A,Bを任意の命題を表すとすれば、このような推論図で1つの推論規則を表したことになります、これを日本語で構成的仮言的三段論法と言います。以下例です、


(A→(B→C)というのは(A→(B→C))の書き間違えです。
すべての仮定が取り除かてしまった上のような演繹を証明と呼びます。
特に証明を図式的に表されていることを強調したいときにはそれを証明図と言います。(演繹と証明は区別してもしなくても…という感じはあります)
また、演繹または証明に用いいられる推論には2つの種類があります。
その一つは<→の導入に関する推論規則>もう一つは<→の除去に関する推論規則>です

これもいくつか具体例を見てみましょう。
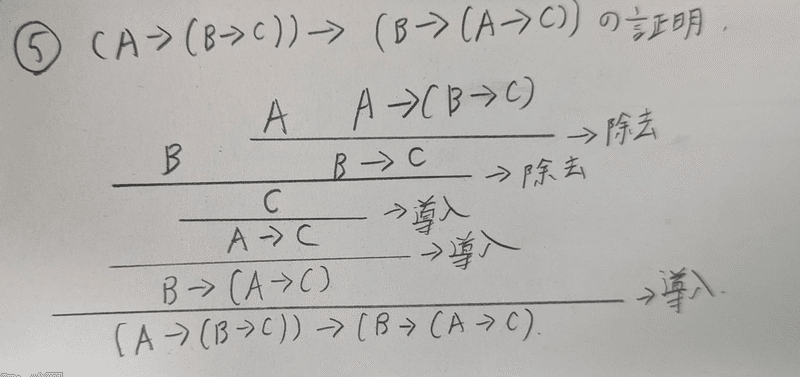

2, ∧について
∧に関してもやはり導入と除去が考えられます

例


3、∨について
∨に関してもやはり導入と除去が考えられます。

が成り立つことと同じ意味
除去の推測規則は場合分けの証明を意味しています。
A∨Bというときに、A→C またB→Cならば成立という二か所の証明が必要です
例

4、¬について
Aの否定である¬Aというのは命題Aが間違っているということを意味している命題です。では、どのようにしてAが間違っているのかを示すのかというとここで矛盾(人)が出てきます決して人間の人ではないです、となると次は矛盾とは何か?という事になりますが先に結論を言うとある命題Aと否定命題¬Aが同時に存在する事を意味しています。この矛盾命題人を用いると
¬に関する推論規則は次のようになります。
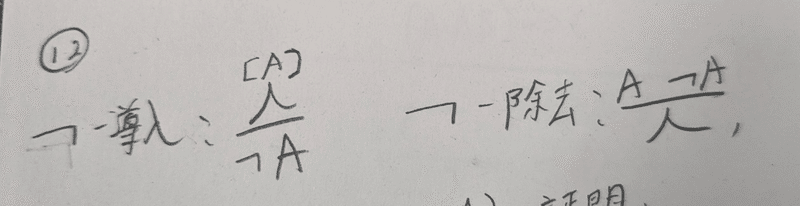
例


5,∀について

変数条件 ∀-導入を用いる場合にF(a)に至る仮定すべて、並びにF(x)の中に自由変数があってはならないというルールが存在します(これについては割愛します)
例


6、∃について

変数条件∃も∀と同じようにaとしてあらわされている自由変数はF(x)およびCに含まれてはいけないルールが存在します(こちらも割愛)
例

3,真理値
命題の真偽を表すために、我々は真理値というものを用いることがあります
正しい命題 には T
間違った命題 には F
という記号を対応させる、Tは真(True) Fは偽(False)という名称があります。
真理値の基本事項
1,演繹法で証明された命題はすべて正しい(2章の例はすべて正しい)
2,Aの否定¬Aの真理値がTであったときだけAの真理値はFであります。
命題ごとに真理値を対応させた表の事を真理表と言います
理解するには例を見たほうが早いかもしれません

4,トートロジー
今
$${((A→B)→A)→A}$$
とか
$${(a→A)→[((A→B)→a)→A]}$$
とか
$${(P→(Q→R))→((P→Q)→(P→R))}$$
という命題を考えてみますこれらはいずれもA、あるいはA,B(P,Q,R)の真理値が何であってもTという真理値を持つことがわかります、実際に真理表を作ればわかります。(自分で作ってみてください)
このように命題の真理値が何であっても、その真理値が常にTとなるものを常に真な命題結合またはトートロジーと呼びます。
(関係ないですがトオトロジイダウトフルという曲があります、主の好みの曲なのでぜひ聞いてみてね!!!)
トートロジーに関する性質を2つ紹介します。
一つ目 トートロジーはすべて演繹法によって証明することが出来る。
二つ目 ∀や∃を用いない古典命題論理の範囲ならば、すべてのトートロジーは証明することが出来る。
以下はすべてトートロジーであるので自分で確かめてみてください。
$${A→A}$$
$${¬(A∧¬A)}$$ [矛盾律]
$${¬(A∧B)⇄(¬A∧¬B)}$$
$${(A→C)→((A→B)→C)→C)}$$
5,ド・モルガンの証明
最後にド・モルガンの4つの式を証明して終わります。
中学校で習ったド・モルガンの法則を記号論理で表すとこんな感じです
また下二つもド・モルガンの法則と呼ばれています。

各命題の証明です。




終わりに
ここまで記事を読んでくださりありがとうございます!!もし、記号論理学についての知見が少しでも身についたor広がったというならとてもうれしいです(謎目線)。時間の関係で3パート重要な所と4パートより複雑な話を入れたかったのですが入れられなかったのでこれはまた別記事で書こうかなと思っています。疲れました(2徹)!!!こんな環境で打ってたので間違えているところとかもあるかもしれません(発見した時はDMください)。
これで僕の記事は終わりです。ではまた次の機会に会いましょう。
参考文献 記号論理入門 新装版(日評数学選書)
この記事が気に入ったらサポートをしてみませんか?
