
【WS】キャンセル確率を実際に考えてみる【ヴァイスシュヴァルツ】
ヴァイスシュヴァルツプレイヤーの方、はじめまして。
デュエマスラム街出身のchapuddingです。
パズドラTCGが復活すると騙されてヴァイスを始めることになり、でかい大会の3人チーム戦に連行されることになりました。
でかい大会に出るからにはきちんと練習をしよう、ということでここ二週間ほどチーム組む相方や高校の同期に練習させてもらってます。
7月上旬は7月16日開催されたデュエルマスターズの大型公式大会である超CSに向けて練習を続けていたためヴァイスシュヴァルツの練習はほとんどできず、8月19日に開催されるトリオサバイバルまでの1ヶ月の間にゲームのルールやカードのテキストもままならない状態から仕上げる必要がありました。
そのため、先日も仕事終わりに公認大会へ練習しに行ったのですが確率面で非常に困ったシーンに遭遇してしまいました。
それこそが今回の題目である攻撃のキャンセル確率ですね。
デュエマやポケカからくる感覚的な確率を頼りに練習してきた僕はどう殴れば良いか判断できず直感で殴った結果、裏目を踏んでしまい負けました。
どちらの選択がより勝率が高いのかを試合後になって考えた際に、攻撃のキャンセル確率の計算が複雑なためその場では判断しきれませんでした。
そこで、山札の総数とクライマックスの枚数によってキャンセル確率がどの程度変化するのか実際に調べてみました。
まだヴァイスシュヴァルツを始めて1ヶ月未満程度の知識しかないため、誤りなどあるかと思います。
もし誤りがありましたらご連絡ください。
X(旧Twitter): @chapuddingEA
問題の場面
「甘美の零龍喚士・ネイ」3面での詰めにおける最終局面、3体目の攻撃の前で相手は3-2まで押し込まれていた。

お前こんな性能だった?
アタックトリガーの4点バーンと1点以上入れば勝ちで相手のクライマックスは墓地に6枚、マナに1枚噛んでいる。
山札に残り1枚があったとしてもソウルアイコンを7枚中6枚捲れた場合本体の打点が通れば確実に勝てる状況だった。
相手は前のターンに手札誘発である「メイド服姿のチノ」を墓地から拾っていたため、こちらの最初の二回の攻撃はサイドアタックで手札誘発を回避していた。

この女が世に放たれてから12年経ってるらしい
この手札誘発を打たれると墓地のカードが全て山に帰るため、フロントアタックをした場合はマナに噛んだ1枚と墓地の6枚の計7枚のクライマックスが戻った相手の山札と「甘美の零龍喚士・ネイ」本体の打点の勝負になる。
一方で、攻撃できる「甘美の零龍喚士・ネイ」の正面のクリーチャーのレベルは3であったため、手札誘発を避けるためにサイドアタックをした場合は本体の打点を通すためにトリガーチェックでソウルアイコンを捲る必要があった。
言い換えるなら、この局面でのサイド・フロントの攻撃選択は以下のうち確率が高いものを選択する問題であった。
31枚の山札の上から3or4枚の中にクライマックス(7or8枚)が含まれていない確率
35枚の山札からソウルアイコン付きカード(20枚)を捲る確率
この両者を比べた際に後者が約57%程度だとすぐ理解できたため、前者よりは確率が高いであろうと判断してサイドアタックを宣言した。
アタックトリガーは6/7ソウルアイコンだったため最大値のバーン、山札にあった8枚目のクライマックスで二回のバーンのうち片方を防がれて3-6に上がる。
結果として最後のトリガーチェックでソウルアイコンが捲れず、本体の打点は0点で止まりターンを返すことになった。
確率暗記の重要性
突然だが、40枚の山札の上から5枚を見たときに4枚採用のカードが1枚以上ある確率は何%かわかるだろうか?
答えは約43%である。
これはデュエルマスターズにおいて、もはや知らない人間は競技プレイヤーではないと言えるほど常識的な数字である。
何故なら、この確率はアグロに対する回答を特定の1種類のシールドトリガーに依存しているデッキがそれをシールドから実際にトリガーできる確率だからだ。
現代デュエマでは巨大天門などがこれに該当しており、巨大天門が赤緑アポロや赤単我我我に不利と言われている論拠はここにある。
このような確率を予め知っておくことで、対戦内外で時間や思考力などの不要なリソースを使わずに済む。
そのため、ヴァイスシュヴァルツにおいてもダメージが通る確率を知ることは非常に有意義であると考えた。
ダメージの通る確率の計算方法
$${n}$$枚の山札のうち$${k}$$枚がクライマックスの場合、$${x}$$点のダメージが通る確率は、次の確率を計算することになる。
「$${n}$$枚のカードから$${x}$$枚のカードを同時に選んだとき、$${k}$$枚あるハズレを1枚も引かない確率」
この確率は以下の計算式で求めることができる。
$$
\frac{_{(n-k)}{\mathrm C}_x}{_{n}{\mathrm C}_x}
$$
具体例
15枚の山札にクライマックスが4枚あることがわかっているとき、2点の攻撃が通る確率は以下のようになる
$$
\frac{_{(15-4)}{\mathrm C}_2}{_{15}{\mathrm C}_2}=\frac{_{11}{\mathrm C}_2}{_{15}{\mathrm C}_2}\simeq 0.524(52.4\%)
$$
すなわち攻撃が通る確率は約52.4%であり、キャンセルする確率は100%-52.4%=48.6%となる。
冒頭の場面の正解択
確率の計算方法がわかったところで、一番最初に提示した場面での正解択について吟味する。
再度、2つの選択肢の確認をしておこう。
31枚の山札の上から3or4枚の中にクライマックス(7or8枚)が含まれていない確率
35枚の山札からソウルアイコン付きカード(20枚)を捲る確率
ここでフロントアタックを宣言した場合、相手の残り1枚のクライマックスが山札にあったときに攻撃が通る確率は以下のように計算できる。
$$
\begin{array}{lll}
&\frac{_{23}{\mathrm C}_3}{_{31}{\mathrm C}_3}\times \frac{15}{35}&(ソウルが乗らない場合)\\
+&\frac{_{23}{\mathrm C}_4}{_{31}{\mathrm C}_4}\times \frac{20}{35}&(ソウルが乗る場合)\\
\simeq &0.330&(33.0\%)
\end{array}
$$
次に、相手の残り1枚のクライマックスが手札にあった場合に攻撃が通る確率は以下のように計算できる。
$$
\begin{array}{lll}
&\frac{_{24}{\mathrm C}_3}{_{31}{\mathrm C}_3}\times \frac{15}{35}&(ソウルが乗らない場合)\\
+&\frac{_{24}{\mathrm C}_4}{_{31}{\mathrm C}_4}\times \frac{20}{35}&(ソウルが乗る場合)\\
\simeq &0.386&(38.6\%)
\end{array}
$$
これらの確率から、フロントアタックをした際の勝率は33〜39%であることがわかる。
サイドアタックをした際の勝率は57%であることから、今回のシーンはサイドアタックをすることが正解だということがわかった。
フロントアタックによる勝率が50%はあると考えていた私にとって、この結果は正直なところ想定外であった。
結果として勝率が高い方を選択できたためサイドアタックを宣言したことはプレイミスではなかったものの、もし無知が故に20%弱も勝率の低い選択肢を本番に取ってしまったら悔やんでも悔やみきれない。
そういった無くせるプレイミスを無くすためにも、確率をあらかじめ知っておくことは重要なのだ。
早見表
特定のシーンにおける確率を知っていても仕方がないため、山札の総数とクライマックスの枚数ごとに攻撃が通る確率を一覧化した。
表の左下ほど山札の濃度(山札の中のクライマックスの割合)が高い状態であり、表のセルが赤いほど攻撃が通らないことを表している。(より詳細な表は記事の末尾に付する)

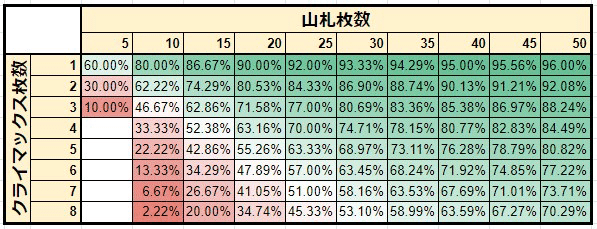


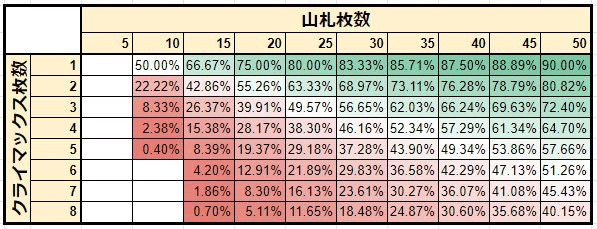
この表の解釈の仕方は様々ではあるが、まず一つ言えることは濃度が同じであれば攻撃の通る確率はあまり変わらない、と言うことだろう。(例えば、4/25の通る確率と8/50の通る確率は概ね同じ)
これは、マナに噛んだクライマックスを掘る行為にどの程度妥当性があるかを判断する材料になる。
濃度が変わらないにもかかわらず多くのリソースをマナの消費に資する行為はキャンセル確率という観点からは悪手であると言える。
また、クライマックスの枚数が変わらない場合、山札が5枚減るとキャンセル率は8〜10%前後上がることがわかる。(6枚差は約10〜12%)
これは、リフレッシュする際に山札に戻る枚数である20〜35枚のときに言える傾向であり、リソースを絞ってでも1-6リフレッシュや2-6リフレッシュをするべきかの基準になるだろう。
キャンセル率を12%あげることがクロック2ドローを放棄するに値するのか、逆にクロック2ドローがキャンセル率を12%下げるに値するのかを状況ごとに吟味していく必要がある。
クライマックス濃度による確率の近似
この早見表を丸暗記して実践に活かせるプレイヤー限りなく0に近いだろう。
何故なら早見表の丸暗記に費やす時間は実際の練習時間に費やした方が有意義であり、対戦中に1%未満の厳密な確率について吟味する時間でプレイを早くした方が時間切れによる両負けのリスクを減らせるからだ。
それよりも、対戦中に大雑把な確率を簡単に導ける程度の知識を知っておくだけの方が、練習時間を確保できる上に10%単位の精度なら簡単に選択肢の比較ができるようになる。
クライマックスの濃度が同じであればある程度攻撃の通る確率は同じであるという傾向が早見表からは読み取れたため、クライマックスの濃度に焦点を当てて議論をする。
$${n}$$枚の山札のうち$${k}$$枚がクライマックスの場合、$${x}$$点のダメージが通る確率は、次のように計算することもできる。
$$
\begin{array}{lll}
&\frac{n-k}{n}&(1点目が通る確率)\\
\times &\frac{n-k-1}{n-1}&(2点目が通る確率)\\
\times &\frac{n-k-2}{n-2}&(3点目が通る確率)\\
\times &\cdots\\
\times &\frac{n-k-(x-1)}{n-(x-1)}&(x点目が通る確率)\\
=&\prod_{i=1}^x\frac{n-k-i+1}{n-i+1}
\end{array}
$$
ただし、$${\prod_{i=1}^x}$$は$${i=1\sim x}$$の総積を表す。($${\sum_{i=1}^x}$$の掛け算版)
ここで、山札の枚数$${n}$$とクライマックスの枚数$${k}$$が十分に大きいことを想定する。
例えば500億枚の山札のうち80億枚のクライマックスがある場合、そこから3枚クライマックスを引き抜いたところで攻撃が通る確率にはほとんど影響がないことが想像できるだろう。
このように、$${n, k}$$が十分に大きいとき$${n-x}$$はほとんど$${n}$$とみなせる。
以上の想定の元、クライマックス濃度を$${p=\frac{k}{n}}$$としたとき、上記の攻撃が通る確率は以下の式のように近似することができる。
$$
\begin{array}{lll}
&\prod_{i=1}^x\frac{n-k-i+1}{n-i+1}\\
\simeq &\prod_{i=1}^x\frac{n-k}{n}&(\because i, 1 \ll n)\\
=&\prod_{i=1}^x (1-p)\\
=&(1-p)^x
\end{array}
$$
この近似によって、大雑把ではあるものの攻撃の通る確率を対戦中に軽く導出できるようになる。
例えば、山札13枚のうち2枚がクライマックスの場合、4点の攻撃が通る確率を考える必要があるシーンを想定した際に、以下のように概算できる。
13枚中2枚ならば104枚中16枚程度濃度のため、クライマックスの濃度$${p}$$は15%程度
$${1-p}$$の値はおよそ85%程度
85=17x5であり17x17=289であるため、$${(1-p)^2}$$はおよそ72%程度
0.72x0.72は0.7x0.7より少し大きい程度なので$${(1-p)^4}$$は50%程度
上記の手順で実際にどの程度の時間がかかったかを想定するために、サイコロで山札の枚数とクライマックス枚数、ダメージ数をランダムに決めた直後から概算が終わるまでの時間を計測したところ、30秒ちょっとで概算できた。
実際の確率は約46.2%であり、誤差は5%弱であった。
以上のような簡易的な実験を5回ほど繰り返した際の結果を以下に示す。(カッコ内の数字は左から順に山札の枚数、クライマックスの枚数、ダメージを表している。)
(13, 2, 4): 31秒, 予測: 50%, 実際: 46.2%
(43, 7, 2): 25秒, 予測: 72%, 実際: 69.8%
(18, 1, 4): 19秒, 予測: 80%, 実際: 77.8%
(44, 2, 3): 33秒, 予想: 84%, 実際: 86.7%
(49, 7, 2): 22秒, 予想: 72%, 実際: 73.2%
このように、この近似式を用いることで25秒前後の時間で誤差5%程度の近似ができた。(個人差あり)
枚数を数える行為込みでも1分程度で概算できるため、確率を吟味しなければならないシーンに直面した際にも現実的な時間の長考で検討が可能になる。
視覚的に確率を記憶したほうが早いという方は、近似式をグラフにしたものを見て覚えていただきたい。

ただし、これはあくまでも近似値であり実際に攻撃が通る確率よりも高い近似値が表示されている。(証明略)
例えば山札25枚のうち7枚がクライマックスの場合(理想的な状況での1-6リフレッシュを想定)、実際に3点の攻撃が通る確率は35.5%だがこの近似では37.3%となる。
おわりに
今回は、ヴァイスシュヴァルツにおいて実際に攻撃が通る確率について考えてみた。
今回議論した細かな確率が実践で必要になる場面に出くわす頻度はほとんどないが、知識として実際に確率を知っている状態はアドバンテージになり得るだろう。
攻撃が通る確率に限らずカードゲームにおいて確率とは切っても切り離せないものであり、体感確率と実際の確率に乖離が生じている状態は適切な判断を下せない状態であるともいえる。
この記事を機に、カードゲームにおける確率に興味を持っていただければ幸いである。
おわり
おまけ





この記事が気に入ったらサポートをしてみませんか?
