OMC217 参加記
こんばんは。
本記事では2024/4/9に開催されたOMC217の感想などを書いていきます。
奇数ナンバリングでの無印回、OMC137(2022/12/12)振りらしいです。
前回書き忘れましたが、チーム戦はスタートダッシュを決めることができたので、継続したいなと思ってました。
問題ページは以下です。
参加時の動き
配点は 2-2-4-4-4-6
writer的にnatsunekoさん(組み合わせ、幾何)、funnyfaceさん(不等式)、natadekokoさん(幾何) と最後の問題はパターンがあるなと思っていました。
点数パターンが少なく、できるだけいいスピードで4-4-4を取りたいなという意識。
C

3で割り切れるものは無視して、mod3 で1のものをa個、mod3 で2のものをb個使うとき,f(T)= (b mod2) +1 で、これらの選び方は 3000Ca*3000Cb
aを0~3000で動かすことで
2^3000*3000Cb*1(b偶数)の和 と 2^3000*3000Cb*2(b奇数)の和
を求めればよい.Σ3000Cb(b偶数)=Σ3000Cb(b奇数)=2^2999 なので(二項定理)f(T)の総和は2^2999+2^3000 とおもいきや、空集合はなぜか例外視しているので2^2999+2^3000-1 全体では 2^3000-1通りの選び方がある。
空集合を除外してきれいなものが汚くなっているな~と思っていつも通り計算しようとして見るが、問題を見るとなぜか分子だけ聞いている。さらに既約かどうかが怪しい。(writerを見て注意深く見るようにしてました)
x=2^2999として互除法していると案の定19を発見 19^2がダメなことをオイラーの定理で確認
ここまで行けばあとは計算 空集合さえ除外しなければこんな汚いことにはならなかったのに、という反面教師的な題材?分野はCとなっていますがNが本質
D

幾何はいつもなら飛ばすが、求角ということで、最悪三角関数での立式をして当てはめれば何とかなる、ということで取り組む。
角度が同じところが気になったので、APとBCの交点をXとする
XB=XAなる二等辺三角形が出てきて、BCを軸にAを折り返した点をDとすると、ABDの外心がXになる。同様にPを折り返した点をQとすると、A,B,Q,Cが共円で、AQ=BQが得られる。AD=BDなのでABDが正三角形となるので、PBC=15/2°
折り返しでいい感じになることに気づけたのは運がよかったけど、それが無理なら三角関数で立式してたはず。
OMCでは珍しい、正統派の角度の難問
E

f(k)=Σ[n/2^k]*2^k である。ここで
g(n)=-1000n+Σ[n/2^k]*2^k = -1000n+Σ(n/2^k-nmod2^k)2^k)
=n-Σ(n mod 2^k)
nをbit表記して、増減を見てみる。
2^1000+36に対して計算すればよい。36 = 2^5+ 2^2に注意して計算。
f(k)定数ずらして1ペナ
指数に対して mod 997 してしまい1ペナ
2冪の近くでは小さく減るので、上位数件分は最終的に大きい方から数件と一致するというのは面白い。
A

判別式はn^2-6n+57=(n-3)^2+48でこれが平方数
48=(x+n-3)(x-n+3)で、差が偶数
B

AB:BC:CA=|ABP|:|BCP|:|CAP|なので、Pは内心。半径r,AB=3x,BC=4x,CA=5x
として,各接点への距離は 2x,3x,1xとなる。とくにBPはsqrt(r^2+x^2)で、面積の条件から6xr=768
ヘロンの公式でxが求まると思っていたが、よく見たら3:4:5なので直角三角形。r=xである。
F

zについて式を整理すると一応zの二次式にはなるけど、係数がとんでもないことになるので、違いそう。
分子を定数にして分数内の変数を減らそうとしてみると
1/(1+y^(1/2)/x)+1/(1+z/y)+1/(1+x^(3/2)/z)=1となる。
]新たにa=y^(1/2)/x,b=z/y,c=x^(3/2)/zとすると、
z=1/(a^6b^3c^4)となり、制約は1/(1+a)+1/(1+b)+1/(1+c)=1
となる。分数が煩わしいので、1/(a+1)=1-a/(a+1)=1-1/(1+1/a)という変換から、1/aを新たにaと置きなおすことで
1/(a+1)+1/(b+1)+1/(c+1)=2という制約のもと,z=a^6b^3c^4を最大化することとなる。zの微分が楽そうなので、ここでラグランジュの未定乗数法をしてみると
6z/a=-λ/(a+1)^2,3z/b=-λ/(b+1)^2,4z/c=-λ/(c+1)^2,となる。
(まず、z/aとするところをzaとしてしまい、三次方程式の解となって迷走していた)
上記制約から、6(a+1)^2/a=3(b+1)^2/b=4(c+1)^2/cと制約を満たすa,b,cを求める。上の等式の値を12tとする。
(x+1)^2=xc⇔x=((c-2)±sqrt(c^2-4c))/2
1/(x+1) = (1±sqrt(1-4/c))/2
となる。(コンテスト中は個々の符号が-しかありえないと思って解が求まらず迷走していました…)
実際には
(1±sqrt(1-2/t))/2 + (1±sqrt(1-1/t))/2 + (1±sqrt(1-4/(3t)))/2 = 2
⇔±sqrt(1-2/t)±sqrt(1-1/t)±sqrt(1-4/(3t)) = 1
なるtと符号を決める必要がある。分数がいやなので1/(3t)=sとすると
±sqrt(1-6s)±sqrt(1-3s)±sqrt(1-4s) = 1
-,+,+のとき,s=280/2209となる。(この辺は落ち着いて式変形すればそんなに重くないはずだができず…)t=2209/840でそれぞれa,b,cを求めると
a=35/12,b=5/42,c=7/40となる。
模範解では上記での1-1/(a+1)をaと置きなおして、
a+b+c=1の下で((1-a)/a)^6((1-b)/b)^3((1-c)/c)^4 の最小値を求める→相加相乗にうまく分解という流れだった。
この方の作問力、あまり触れている人を見かけないけど、数オリっぽさの強い問題が多くて、相当凄いと思う。
感想と反省
5問正解63分17秒1ペナで7位でした!Fで力負けしてしまい悔しい結果に。
ただ、D,Eがそこそこ難しかったため、総合順位としては悪くない出来になりました。立ち回り自体はそこまで問題なかったですが、強いて述べるならEのペナルティ関連でしょうか。Fのラグランジュの計算はもっと強くなっておきたいと思える内容でした。
全体的には計算が重めor計算で逃げられるみたいな問題が多く、Dで初等解を見つけていながらも腕力が試されるセットと感じました。ただ、計算が重いから悪い問題というわけではなく、いい問題でした。前回のOMCB004 との難易度差が大きく、個人的には割とexpertに近い感覚でした。
個別の問題を見るとD,E,Fはどれも面白い問題で、計算での逃げ道があるものの、スマートな証明方法を含んでいて面白かったです。C問題は本質が整数でわざわざ空集合を外す不自然なことをしてまで計算させるというのがあまり好きではないですが、これくらいの計算はできてしかるべきというメッセージにも思えました。
チーム戦も引き続き好調の模様で、安心しました。無論勝ちたいというのはあるのですが、参加者に程よい緊張感と程よい楽しさがあるといいなと主催者でもないのに勝手に思ったりしてます。(なので、前にも言及した通り、同じ人のスコアがずっと計算されているのは微妙だなと思ってます。橙の人の25位と参加者の真ん中くらいの緑~水の人の50位が同じという計算でそれは少しおかしいかなと思ってます。)
難易度が高めの出題だったので、チームメンバーがマイナスの気持ちになりすぎてないといいと思いつつ、次回以降も頑張りたいです。
雑多なトピックス
前回に引き続き、分野ごとのOMC特徴づけを個人的見解に基づき列挙していきます。今回は最後、整数分野について書いていきます。
4回分書いてきた内容をちょっとだけ整理して、OMC分野別攻略、という感じで一個の記事にまとめるかもしれません。(再放送でさぼる手法)
まず、前提の特徴として以下が挙げられます。
・難易度の低い問題はそれほど特徴はない
OMCの作問のページにおいて、ストック数を確認できるのですが、際立って多いのがN分野の200点の部分です。数だけでなく、問われる内容的にもそこまで差異がないです。簡単な証明を求値化しやすいという感じでしょうか。
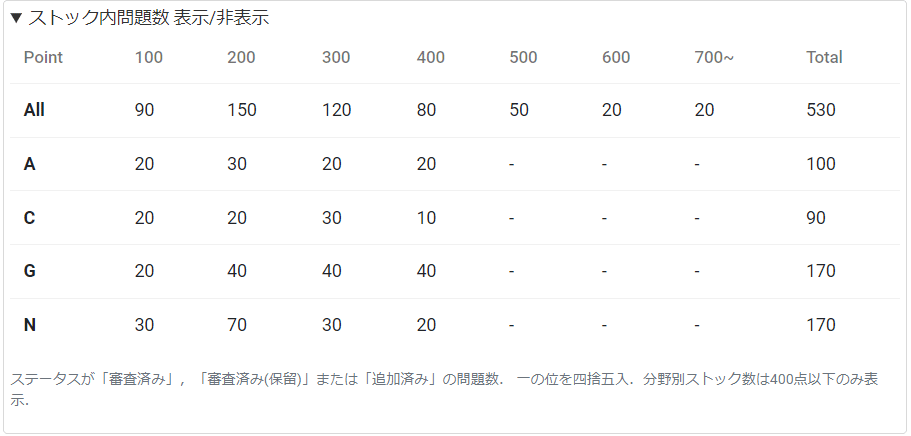
・高難易度が少ない
高難易度だと求値化しにくい証明やC分野のような問題、関数方程式などが多く、OMCではそもそも難易度の高い問題があまり出ていません。難しい問題もありますが、出題ネタが絞られていたり、他分野との複合での出題のイメージがあります。そもそも整数の難しい問題を作問する人が少ないというのも要因としてはありそうです。(複合でない整数論の難問は殆どjun2nosimobeさんが作っていて、writerから一個ずつチェックする方が対策としては速いと思います。逆に、作問として未開拓な部分も多いかと思います。)
また、整数論自体が少しでも踏み込むと一気に高級な道具を要するという傾向があるため、高校範囲という制約とも少し合わないという傾向もあると思います。
・(分野問わず)各問題の最後の計算の部分や短答化の際に使われる
答えに対して剰余、(正の)約数の数、割り切れる回数などを要求する問題はOMCだととても多いです。2^100みたいな値を直接書けない分、ジャッジ用に非負整数にするために入る作業ですが、必ず持っておかなかければならない知識です。OMCでの登場頻度が特別高いという印象です。
・そもそも、IMOではあまり出なくなってきている
IMOでも整数論はあまり問われなくなってきています。良い難易度のものが出しにくかったり知識で何とかなりやすいというのが原因でしょう。組み合わせに分類してもよさそうな問題が多いイメージです。なんでもかんでもIMOをベースにして語るのはあまり好きではないですが、まあ現状一番権威がある大会(そもそも分野の分け方もここ準拠なので…)ということで、比較対象として言及しておきます。
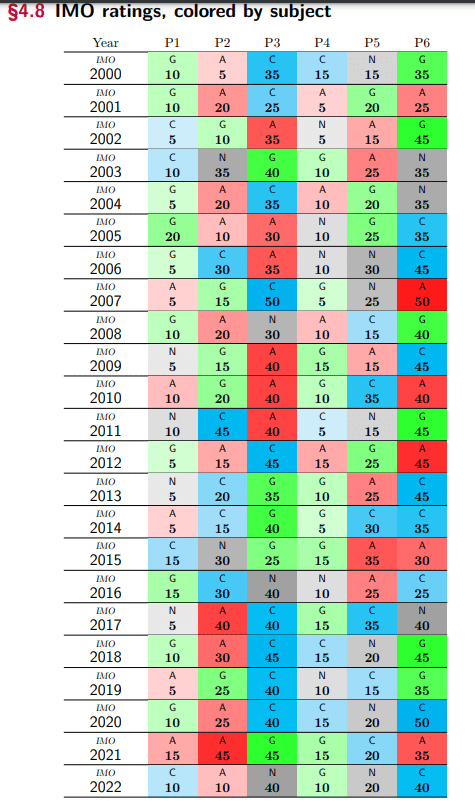
以上を踏まえて、細かい点を見ていきたいと思います。
テーマ分類についてもメモ程度に思いついたものを書いているので、網羅性は期待しないでください
・不定方程式(ディオファントス)
OMCに限らず、N分野のメインと思ってよい範囲です。
-線形
雑なくくりですが、頻出です。ピックの定理をはじめとして格子点数え上げに帰着するものも多いです。
-ベル方程式/二次式
OMCでは直接問われることはあまり無いですが、今後出題されてもおかしくないかなと思ってます。
-ピタゴラス数
ピタゴラス数やその式に類似した二次式の解についても知っておくとよいでしょう。また、ピタゴラス数の解はうまく数え上げることができて、(最近出てませんが)以下の問題をベースにしたものがちょこちょこ出ていたりします。求値化しやすいテーマです。https://onlinemathcontest.com/contests/omc022/tasks/139
-積=定数
因数分解などをして積=定数 という形にして素因数の配分に帰着する問題は頻出です。OMCに限らないテーマです。
-不等式評価
ジャンル分けがあまり同じクラスになっていない表記になってしまいますが、不等式評価で絞り、小さいところで頑張る、というものも多いです。剰余と一緒に使われたりします。a|bでa<=bみたいなところがスタート地点だったりすることが多いです。証明でも頻出で、どちらかというと他分野っぽい式変形などをすることも多いです。
・剰余
短答化の際に問われることが多いこともあって、テクニック/道具が多いです。OMCに限らず、具体数値の問題を作りやすい話なので、頻出です。また、前述の不定方程式の解を絞る際にも頻出です。
-中国剰余定理
頻出ですし、最後の剰余計算でも常識化された道具として使う傾向があります。また、特別なケースでは中国剰余定理の解が楽に求まるというのもよく出たりします。
-最大公約数関連 gcd/最小公倍数 lcm
こちらも頻出です。互除法をはじめ、具体的な数を扱う上では必須の概念です。また、gcdの和は後述するトーシェント関数に書き換えることができて、乗法的関数とみなせるという話もよく出てきます。指数でのmin,maxと思うことで分かりやすくなることもあります。
-平方剰余
あまり問われないですが、知っていると便利、というようなものです。
相互法則は道具としてというよりも証明や応用が面白いので現代数学の入門トピックとして、チェックしておくと楽しめると思います。
-フェルマーの小定理/オイラーの定理
OMCに限らず頻出です。
-ウィルソンの定理
組み合わせの問題で剰余を聞かれたときに問われることがあります。
・付値(ord,v)
割り切れる回数に着目するとうまくいく、ということ自体はマスターデーモンをはじめ、よく知られている話ですが、OMCでもよく問われます。関係のない分野でも問われることがあるのはある種OMC特有かもしれません。
-LTEの補題
個人的には一番特徴的と思っている箇所。OMC以外でももちろん出るには出るのですが、OMCでは際立って頻度が高いなと思います。
-Legendreの定理
階乗の素因数評価。OMCに限らず出ますが、OMCでは特によく出る印象
-Kummerの定理
二項係数の付値。これも道具としてそこそこ出ます。「p-aryで繰り上がりが起こるかどうか」という部分が大事になっています。
・約数の個数d/約数の総和σ/オイラーのトーシェント関数φ/メビウス関数μ
こちらはOMCに限らず頻出の関数です。最低でも計算方法とちょっとした性質は知っておく必要があります。よくある話を列挙するのにとどめておきます。OMC特有の話ではないので、知っておいた方がよいです。また、トーシェント関数の値は手元に表として持っておいてもいいかもしれません。
-約数の総積 n^(d(n)/2)
-φ(φ(n))などの合成したときの性質
-Σ_{d|n} φ(d)=n
-メビウスの反転公式
・数列
代数でも触れたテーマですが、数論的性質を問うことも多いです(Z>0→Zみたいな関数として扱うことも多いです)
剰余での周期や、特定の項の付値、特定の項の各位の和などなど、多岐にわたった問い方があります。「数列」とくくるのはやや雑過ぎるかもしれません。
・関数方程式
離散値の関数方程式が問われることがあります。一般的にこうすればよい、という手法があるわけではないですが、OMCをはじめとする短答形式においては自明な関数のみで出題されることはほぼないので、細かい部分の処理を意識したり、定数ずらした時の挙動をみて普遍的な性質や不等式評価を考える、といったことを意識する感じと思います。
この記事が気に入ったらサポートをしてみませんか?
