
OMC214 参加記
こんばんは
本記事では2024/3/18に開催されたOMC214 (エリジオン杯)の感想などを書いていきます。
なんと5回目のエリジオン杯になります。年度末ではありますが、受験終わりの方が多かったりするおかげか、213から参加者が非常に増えていたので、少しにぎやかになっていいですね。猛者との対決も楽しみですが、運営さんの問題セットなので、そこも楽しみです。
以前まで忙しさをアピールする人になっていましたが、何とか参加の準備もできて、忙しさ要因も大部分解消できて来たので、今後はいつも通りのかかわり方が出来そうです。
問題ページは以下になります。
参加時の動き
点数は1-2-3-4-4-5 時間も80分ということで、わりとbeginnerに近い配点のセット。ただ、賞金付きということで、書いてある数値よりも実際の難易度は高そうだなと思いつつ、後ろの題意把握&解けそうなの数問チョイス→前半倒す→残った問題考察 を意識。
D

係数に法則性がある方程式の問題。テーマとしてはよくある話で、係数を別の変数の多項式で表してうまいこと処理するタイプの問題。
見てすぐに
f(n) = a(10n-1)^4 + b(10n+1)^4 + c(20n-1)^4 + d(20n+1)^4 + 1
と置いて、根が2,3,4,5であるからf(n)=t(n-2)(n-3)(n-4)(n-5)と書けて、あとはf(1)を求めるだけ。実質的にtを求める。ただ、これをそのままやると、結局4変数の1次方程式4つになって、余り状況が変わらない。ただ、この置き方をしたことによって、係数比較をした時にa+b,c+dを文字でおいたら3変数の1次式3つに落ちることに気づけた(偶数次を見る)ので、これを頑張って解いてCA
かなりストレートに処理したので少し自信があったけど、FAには及ばず。
ちなみに、f(n)はg(t,n)=(tx-1)^4とおいて、t=±10,±20の満たす条件とg
(t,n)の係数を見ることで、連立方程式を経由せずとも、係数比較での話と同じ計算を行うことができる
a+b,c+dに着目して変数を実質的に減らし、偶数次を比較する部分の理由付けになっている
ちなみに公式解説の方の多項式がわざわざ分数を根にしててその割に計算が簡単になってるわけでもないので不自然だけど、もとは別の問題だったのかな?
この問題の後、Eを軽く考察して、(実は答えとしては合っている)構成と市松模様の考察を軽く行ったものの、少し自信がなかったので泥沼化を避けてAへ
A
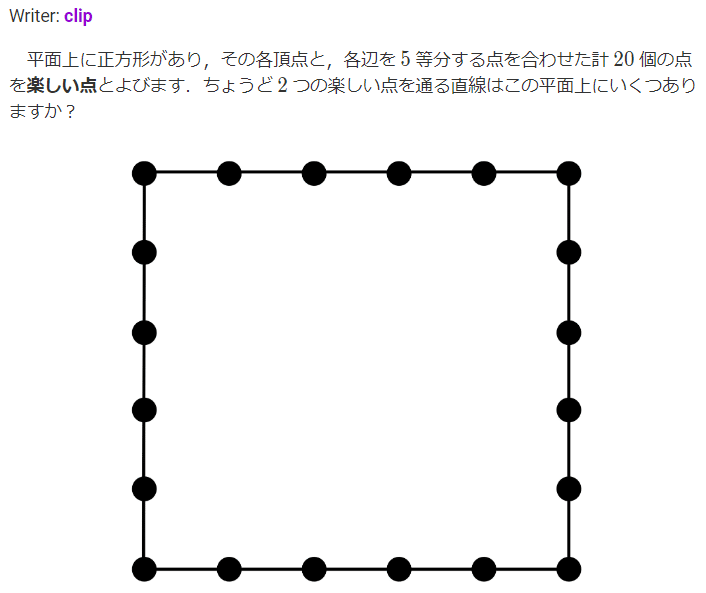
四隅→9 辺→14 (9*4+14*16)/2 「ちょうど」に注意
B

適当に座標を取り、平面の式をおく。それとx^2+y^2+z^2=1を連立してzの最大値を求めた。z、つまりsinをそのまま答えてペナルティ1
四面体書いて解いてる人が結構いて、賢いし幾何脳で見習う必要があると思った。
C

なんかほぼ同じ問題をOMCで何度も見ている気がするけども…
2冪、3冪、6、それ以外をうまく並べる
円環であることを忘れて考察してたせいで、回転一致を同一視せず1ペナ
ところで、分野判定が整数でびっくり。あと300点なの…?
ペナルティが嵩んでちょっと気持ちが沈んでいたけど、まだ本質部ではないので、Fへ(Eの泥沼化が怖かった)
F

図を書いてみてすぐFがミケル点であることがわかり、△DEFが具体的にわかっていて、BCF~DEFと、外接円の半径が169であるところから、BC=240が計算できる。また、DMN~DEBで相似比が13:12で、MN = 12EB/13
さらに、BE⊥CDなので、XE^2+XF^2+XB^2+XC^2=100^2+240^2=2EB^2
で、余弦定理より(XM^2+XN^2-MN^2)/(2XM*XN)を計算できればいいが、
XM=50,XN=120
MN^2 →(144/169)EB^2 = (144/169)*(100^2+240^2)/2
となるので、計算できる。
模範解答通りにすんなり解けていたようで、知識は大事だなと思った。
E

実はDを解いた後、5000+4999+・・・+4902+2451のケースを構成し、50列、51列を数字が大きい方から詰めた後に、分断する1ピース分の数を評価する(≒必ずa以下の書かれたタイルが存在する)という評価をしようとするときに、分断後の右側と左側のタイルの個数がどちらかに偏ることはなさそうで、市松模様に塗るとその辺が評価できそう、ただ特定の配置(大きい方から詰める)に依存した評価で、もしかしたら変な置き方もあるかもしれないと思ったところで泥沼化を避けて飛ばした問題。
Fを解いた後、解いた人数を見たらやけに多かったのであらかじめ計算していた5000+4999+・・・+4902+2451を投げたらCAしてしまった問題。
CA後、上からの評価を考えたが、結局上記の議論で市松模様に塗ったときの同じ色のマスの数の評価に関する議論が、「大きい方から詰める」という手法に依存せず少なくとも2451以下のタイルを含むということが従うので、上からの評価が問題なかったことを確認した。
感想と反省
6問正解40分27秒2ペナで3位でした!ややペナルティが嵩みましたが、相当いい結果になりました。これで、「エリジオン杯」は(3,2,9,7,3)とすべて高順位を保てているので、こういう名前がついている方がよいのかもしれません。
問題セットとしてはちょっと分野の偏りがありました。自分としては、幾何がすんなり解けた分相性は良かったんだと思います。全体的に典型要素を面白く変形して出題されている感じで特に後半は面白さはあったと思います。
個別の問題で見ると、D,Fはそれぞれ典型になる内容をいい感じにひねって出題してあって、面白いと思いました。Dの多項式構成のテクニックやFのミケル点の構図はOMCでも一定の頻度で出ているものですが、そこから面白い感じに数ステップひねられていて、見習いたい出題と思いました。(ただ、どちらも体感よりもdifficulty高いかなと思いました)
Eはコンテスト終了後Xでも話題になっていましたが、問題に対する理解度が低くても構成を雑にやるだけでペナルティ覚悟のエスパーがかなり正当化されてしまうタイプの出題で、問題の内容は結構好きなのですが、こういう問題は出題されない(or後半には置かれない)し、そもそも審査に通らないというイメージだったので、賞金付きのコンテストで出てきたのがとても意外でした。OMC的にどうすればもっと良い出題になったかなとちょっと考えてみましたが、1*mのタイルにするとか、他の列の分も問うとかでしょうか?少なくとも自分の立ち回りとしては、真面目に証明して時間をつぶした人には申し訳ないような立ち回りになってしまいました。
また、今回は、前回の213でのような遅さは全く感じず、むしろ以前よりも順位表がスムーズに見れた気がして、安心しました。
次回は名前付き4bでその後4eと重要な回が続きますが、頑張りたいです。
雑多なトピックス
一個の記事にするか迷いましたが、4回に分けて、A,G,C,Nの各分野のOMCでの特徴を列挙しようかなと思います。すべて個人的観点で書くので、読み手のイメージとは少し異なるかもしれません。今回はA分野について書きます。基本的には数学オリンピックでの記述式の証明問題との比較というのを主な観点とします。
A分野は主に「関数」「不等式」というような分類になっていることが多く、「関数」には関数方程式や多項式、天井/床関数、絶対値などなど 数列や級数を含むこともある という感じです。
OMCでの出題について列挙します。
関数
関数方程式:基本的に解ではなく証明が主体となることが多い分野なので、そもそも出るパターンが限られる上に、あまり頻度も高くないです。
・他分野との複合
数論的な問題(≒数列と思ってよい)であったり、関数の個数を数える話に落とすという問題が多いです。N→Nで特殊な性質込みのもので考えられるものの個数や和を問う、というのが、作問の観点でも多いです。こういう問題は一般化した対策や言及がしづらく、分野判定も難しいところです。
・代数分野
一定の難易度のものは殆ど無いです。解が非自明であることと、予測しにくいこと、などが要求されるためです。逆にOMCをやっていてもこの辺りの練習にはなりづらいと思っていいと思います。
多項式:OMCでは頻出です。複素数も含めた解に対するいろいろな値を問う問題や、多項式の剰余、係数の調整などなど、証明の時よりも具体値で問いやすいので、際立って頻度が高い印象です。JMOなどの対策主体でやってきた人が逆に知らないテクニックなんかも結構多そう。
また、多項式関連の難しい問題は数学オリンピック以外のルーツに相当しそうな問題が多い印象です。
天井関数/床関数などの特定の関数:これもOMCでは頻出です。特定の出題者が好む印象もあります。意外とお手軽に問題を作れたりします。
数列:以下が多いです。
・漸化式とその剰余
これは数列単体というよりも、他の分野での部分問題として頻出です。
・背景に三角関数や図形などのうまい設定が絡む数列
これはOMC特有と思っています。数学オリンピックというよりは受験数学とかで誘導付きで出てくるタイプの問題が起源になってそうな出題です。作問する側としても人工的に難しいものを作りやすいというのが一因でしょう。
母関数:これは分野判定が難しいところですが、結構よく出るイメージです。想定解以外でも含めるなら、頻度も結構高く、かなり強力な武器になるので、習得したいところです。
不等式
OMCでは、不等式の問題は単体では数学オリンピックほど多くは出題されていません。関数方程式の時と同様、すべての変数が等しい時や一つが0の時などに最小値/最大値を取るケースは簡単にエスパー出来てしまうからです。
そうでなくとも、ラグランジュの未定乗数法なんかで少し頑張れば計算できるケースが多いです。また、相加相乗とコーシーシュワルツ(およびRadonなどの亜種)以外が殆ど出題されないので、解く上ではこの二つにアテをつけて変数変換や式変形をするのがよさそうです。逆に不等式での作問を行う際には、変数を増やして上記手法では難しいもの、非自明な値で最小/最大を取るもの、という縛りを入れる方がよいでしょう。
この記事が気に入ったらサポートをしてみませんか?
