GF180でオペアンプ設計してみよう
PDKがオープンソースになってる GlobalFoundries 180 μm (GF180mcuC) で一番基本的な2段オペアンプを設計します.実行しているシミュレーション用のファイルは以下の github リポジトリの opampディレクトリからダウンロードできます.
1.トランジスタの素性を調べる
回路を作る前にトランジスタの素性を知っておく必要があります.アナログ回路設計で重要なのはドレイン電流 Id,しきい値電圧 Vth,相互コンダクタンス gm,出力抵抗 rds (1/gds).まずはチャネル長 L を最小の 0.28 um,MOSのサイズはきりのいいところで W/L=10 にしておきましょう.
しきい値電圧はだいたい 0.7 V前後.ということはこのトランジスタのゲート-ソース間電圧はオーバードライブ100 mV ぐらいとして 0.8 Vぐらいが最も電流効率 (gm/Id) がよくなります.下図のように,オーバードライブはかけすぎると電流が大きくなる割に gm はそれほど増えないので効率が悪くなります.
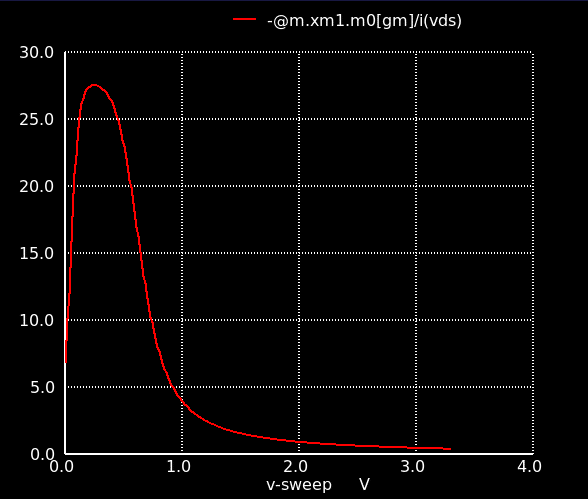
ということで Vgs は 0.8 V,Vds は電源電圧の半分 (1.65 V) として特性を調べると下のような値になります.
$$
\begin{array}{|c|c|c|} \hline
L=0.28 \mu\mathrm{m} & \mathrm{nMOS} & \mathrm{pMOS} \\ \hline
v_{th} & 630~\mathrm{mV} & 720~\mathrm{mV} \\
I_d & 35~\mu\mathrm{A} & 3.3~\mu\mathrm{A} \\
g_m & 260~\mu\mathrm{S} & 45~\mu\mathrm{S} \\
r_{ds} & 110~\mathrm{k}\Omega & 1.3~\mathrm{M}\Omega \\
g_m r_{ds} & 28.6 & 58.5 \\ \hline
\end{array}
$$
しきい値電圧の違いもありますが nMOS と pMOS でかなり特性が違います.nMOS は Intrinsic gain ($${g_mr_{ds}}$$) が28.6 (29 dB)とちょっと厳しい.直流利得は pMOS で稼ぐのがよさそうな雰囲気がします.ちょっと nMOS の rds が厳しいので L を2倍 (0.56 um) にした場合も見ておきましょう.W/L は同じ 10 になるように,W=5.6 umです.しきい値電圧が上がるので Vgs=0.9 V で評価します.
$$
\begin{array}{|c|c|c|} \hline
L=0.56 \mu\mathrm{m} & \mathrm{nMOS} & \mathrm{pMOS} \\ \hline
v_{th} & 710~\mathrm{mV} & 790~\mathrm{mV} \\
I_d & 36~\mu\mathrm{A} & 3.6~\mu\mathrm{A} \\
g_m & 290~\mu\mathrm{S} & 45~\mu\mathrm{S} \\
r_{ds} & 700~\mathrm{k}\Omega & 9~\mathrm{M}\Omega \\
g_m r_{ds} & 203 & 405 \\ \hline
\end{array}
$$
利得を稼ぎたいときは L を大きくすればよさそうということが分かります.
2.全体の構成と設計目標
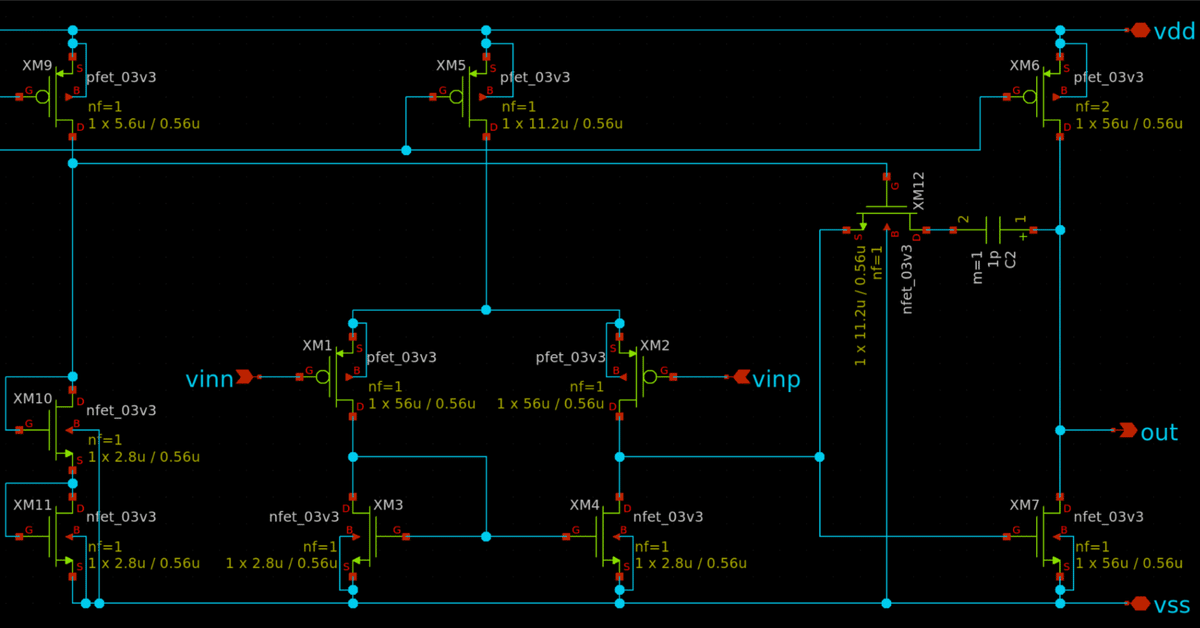
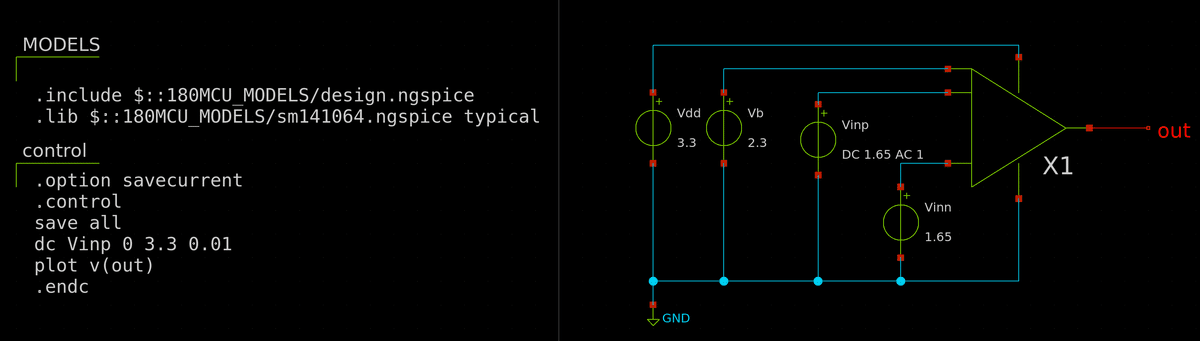
ここでは最も基本的な2段オペアンプを作ります.差動入力段 (初段) と増幅段 (2段目),それに位相補償をかけます.初段は$${r_{ds}}$$が高く電流効率 ($${g_m/I_d}$$) もよい pMOS,を使うことにします.そうすると差動段のテール電流源 (M5) は pMOSになるので,各段に電流を供給するカレントミラーは pMOS で構成することになります (M5, M6, M8, M9).ということで2段目はpMOSカレントミラーを負荷とする nMOS ソース接地増幅回路になります.回路図は下図です.差動増幅 (M1~M5),ソース接地 (M6,M7) 以外にもいろいろトランジスタが使われていますが,これらは順を追って説明します.
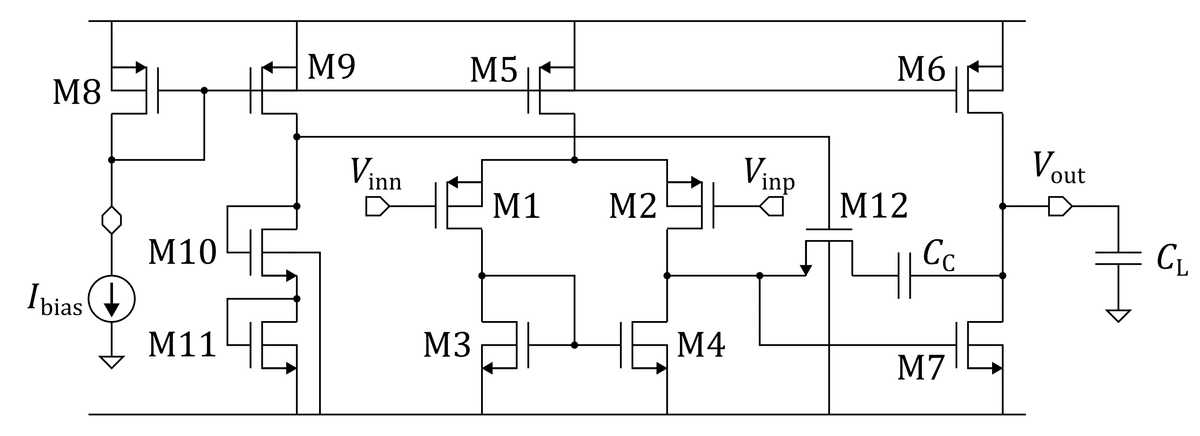
Vinp,Vinn が差動入力,Vout が出力電圧です.バイアス電流として Ibias を使っています.負荷容量は CL です.
3.差動増幅段
差動増幅段 (M1~M5) を設計します.カレントミラー (M3,M4) を能動負荷として使って利得を稼ぎつつ,オフセット除去もできる構成です.オフセット除去については次の節で説明します.
この回路の利得は $${g_m R = g_{m2}(r_{ds2}||r_{ds4})}$$です.トランジスタのサイズはバイアスなどを見ながら決めますが,例えばトランジスタの素性を調べた表より,L=0.28 um のとき,同一バイアス・同一サイズで nMOS は pMOS の10倍の電流を流す能力があります.ということは,M1 と M3,M2 と M4 は同じ電流を流すわけなので pMOS (M1,M2) のサイズを nMOS (M3,M4) の10倍にすると両者のバイアスが同じになります.このとき利得はどうなるかというと,W/L=10 で正規化した pMOS のサイズを $${x}$$ とすると,nMOS のサイズは $${x/10}$$.この関係と表の数値より,利得 $${A}$$ は
$$
A = 45~\mu\mathrm{S}\times x \times (1.3~\mathrm{M}\Omega/x||110~ \mathrm{k}\Omega/(0.1x)) = 26.8
$$
と,MOSのサイズに関係なく定数になります.実際には MOSのサイズを変えるとバイアスが変わるので利得は変化しますが,MOSのサイズ (W) を変えても利得は大きくは変わらない,ということは知っておきましょう.上の計算だと 26.8倍 = 28.6 dB.もうちょっと利得が欲しいので pMOS (M1,M2) を大きくして,M1・M2 の W/L=100,M3・M4の W/L=5 で動かしてみます.テール電流 M5 についてはひとまず W/L=20 にして,Vgs=1.0 V にしておきます.
回路図は必ずテストベンチの部分とは分離して作成します.電源,グラウンドもピンとして定義しておきます.これは LVS をかけるときに必要です.
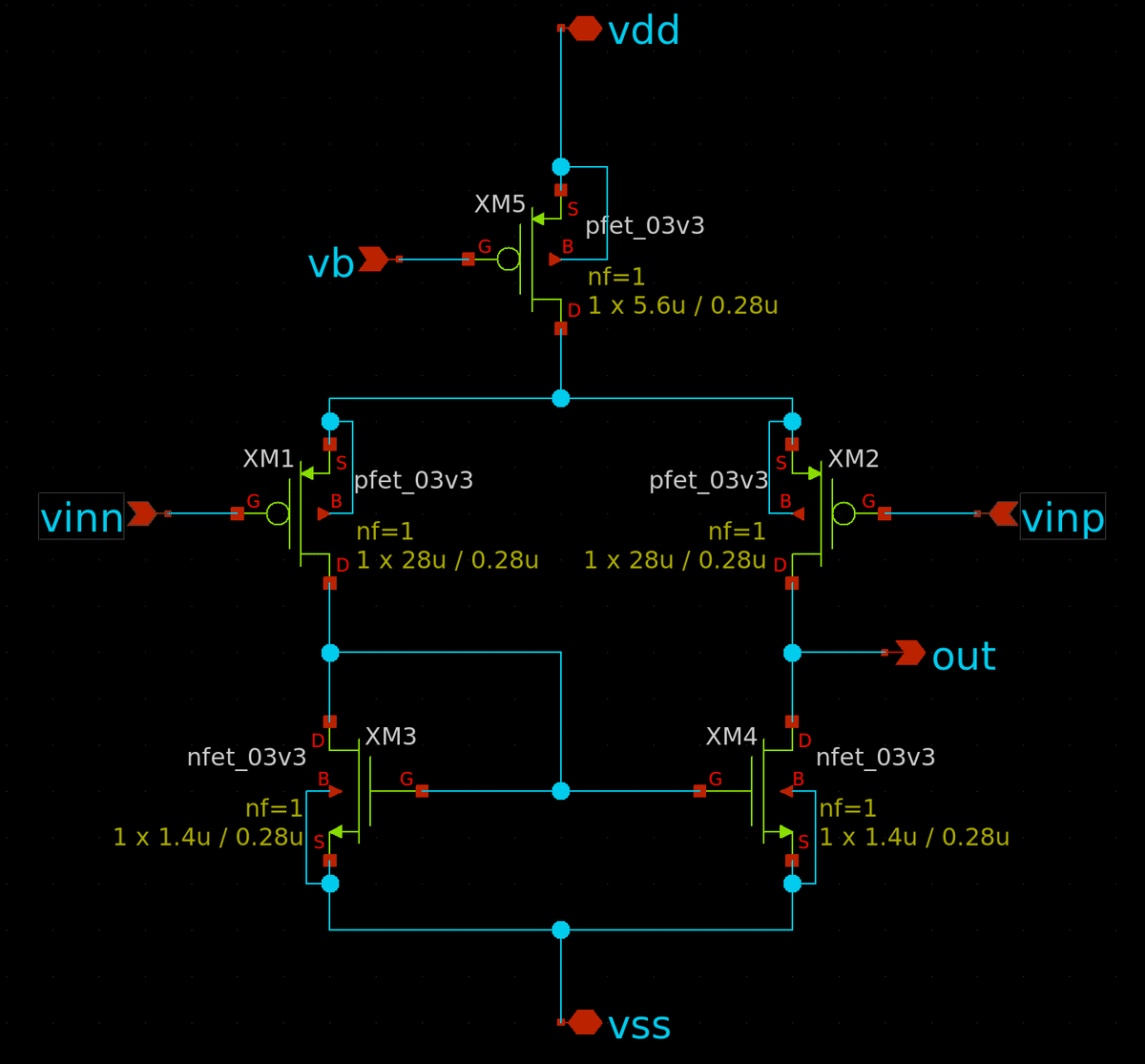
シンボルを作成して (diff.sym),テストベンチを接続します.シミュレーションより利得は 29 dB.ほぼ計算通りです.負荷に容量をつけていないので非常に高い周波数で動くように見えますが,今は周波数特性は気にしないことにします.
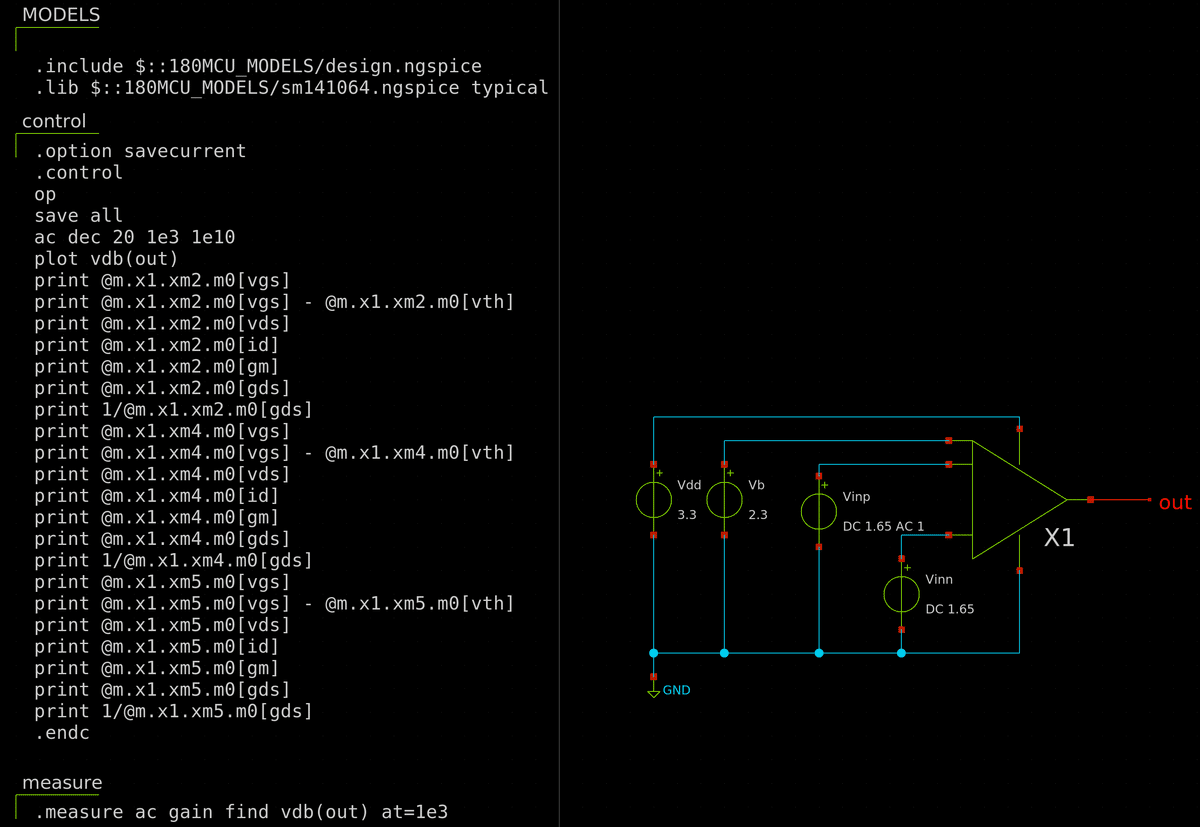
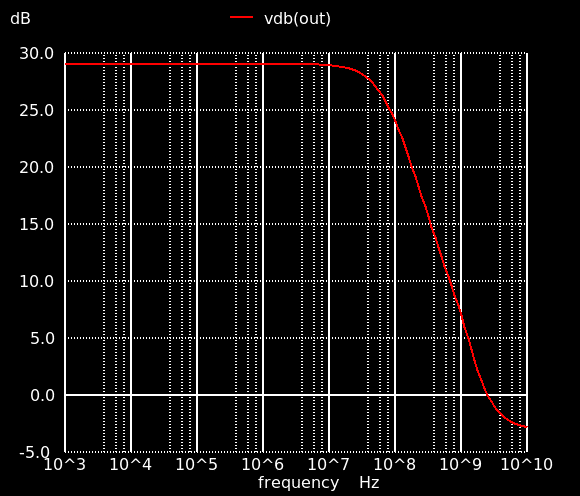
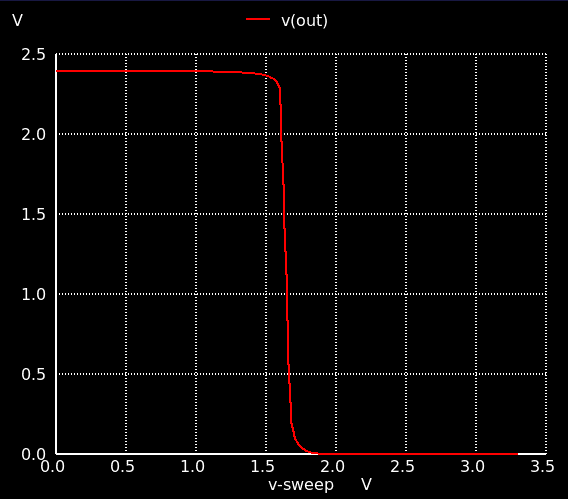
重要なこととして,出力のバイアスを確認しておきます.動作点解析より,M4 の Vds は 0.84 V.2段目が nMOSソース接地増幅段なので,オーバードライブ電圧は 0.2 V程度となり2段目を動かすことはできそうです.バイアスについてはDC解析のテストベンチを作成して確認しておきましょう.下図のようになります.動作可能な出力電圧の上限が 2.4 V程度であることが分かります.
3.ソース接地増幅段
2段目は普通のソース接地増幅回路です.設計のポイントは,十分なスルーレートが得られるように大きな電流を流すこと,システマティックオフセットを0にすることです.
3.1 システマティックオフセットの除去
オペアンプは Vinp と Vinn の差分を増幅する回路です.つまり Vinp = Vinn であれば出力電流は0である必要があります.ここで Vinp = Vinn であるにも関わらず
差動増幅段とソース接地増幅段を接続した回路図は下の通り.
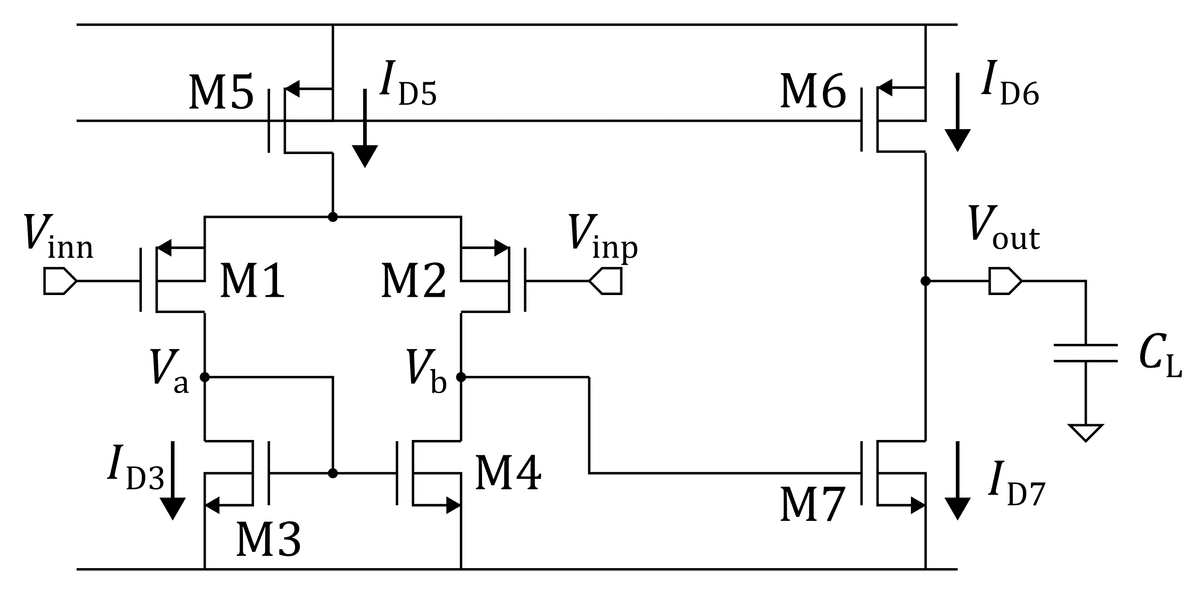
ここで Vinp = Vinn とすると,$${I_{D5} = I_{D3} + I_{D4}}$$ かつ $${I_{D3} = I_{D4}}$$ なので,$${I_{D3} = I_{D5}/2}$$ です.また,$${V_a = V_b}$$ なので,M3 と M7 のゲート-ソース間電圧は等しくなります.つまり $${I_{D3} : I_{D7} = W_3 : W_7}$$ です.一方で M5と M6 はカレントミラーを構成しているので,$${I_{D5} : I_{D6} = W_5 : W_6}$$ です.$${I_{D6} = I_{D7}}$$ であればシステマティックオフセットは 0 になるので,
$$
I_{D6} = I_{D7}\\
\frac{W_6}{W_5}I_{D5} = \frac{W_7}{W_3}I_{D3}\\
\frac{W_6}{W_7}=\frac{W_5}{2W_3}
$$
より,$${W_6}$$ と $${W_7}$$ の比は $${W_5}$$と $${W_3}$$ に合わせておく必要があることが分かります.
どの程度のスルーレートが必要かは用途にもよるのですが,とりあえず nMOSの W/L をキリのいい100 にしてみます.そうすると,pMOS のサイズはシステマティックオフセットを0にする条件から決まります.差動増幅段で $${(W/L)_5 = 20}$$,$${(W/L)_3 = 5}$$ なので,$${(W/L)_6}$$ は $${(W/L)_7}$$ の2倍,つまり200 にすればよいということになります.
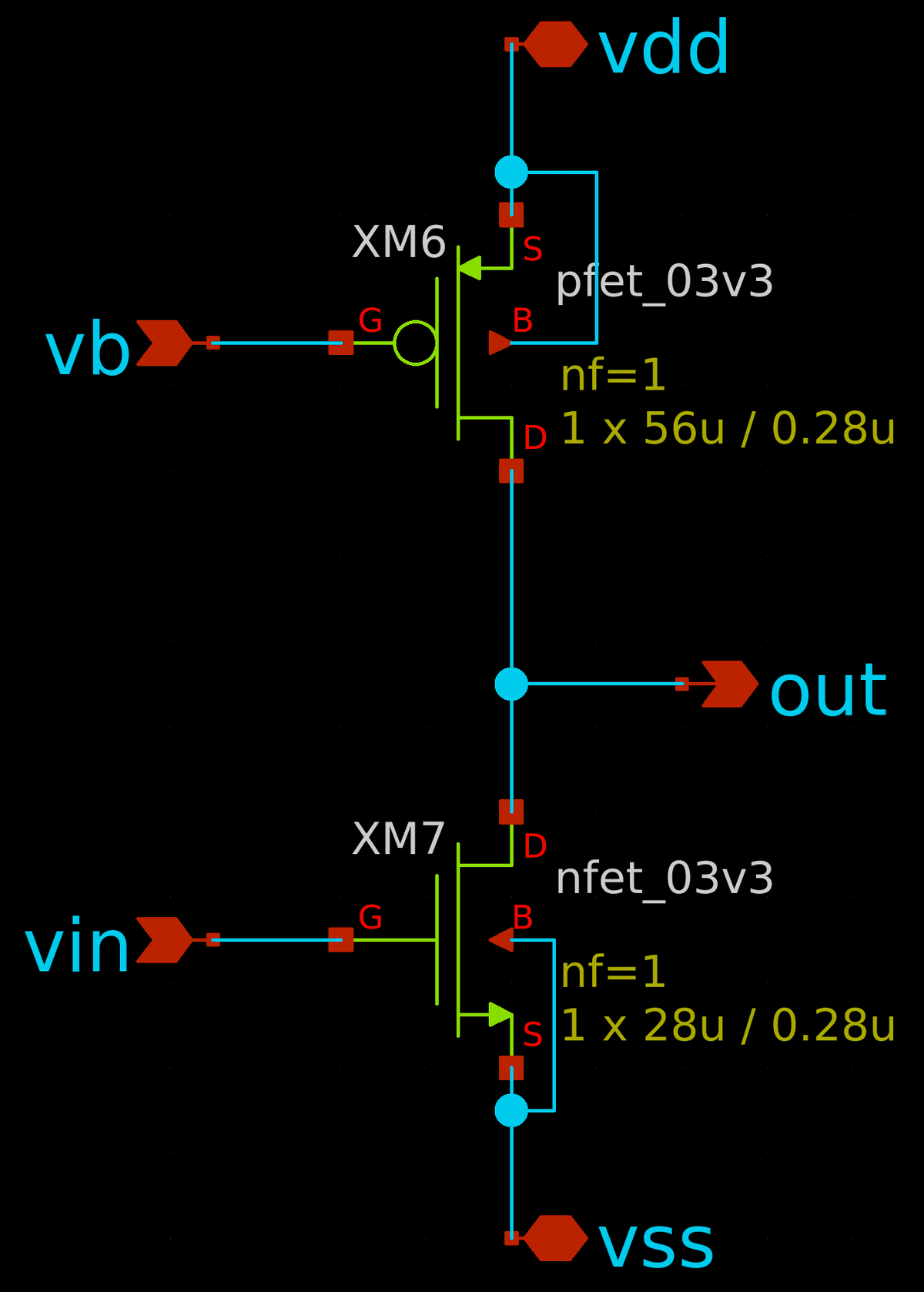
テストベンチを組んで特性を評価します.2段目は出力段ですので,大きな負荷を駆動することが求められます.ということで負荷に10 pF を接続します.直流利得は 24.4 dB.差動増幅段の 28 dB と合わせても60 dB には足りない… ただ,nMOS (M7) と pMOS (M6) の比がシステマティックオフセットによって決まっているため,nMOS の W/L を変えても基本的に利得は変わりません.というわけで,このまま進めることにします.
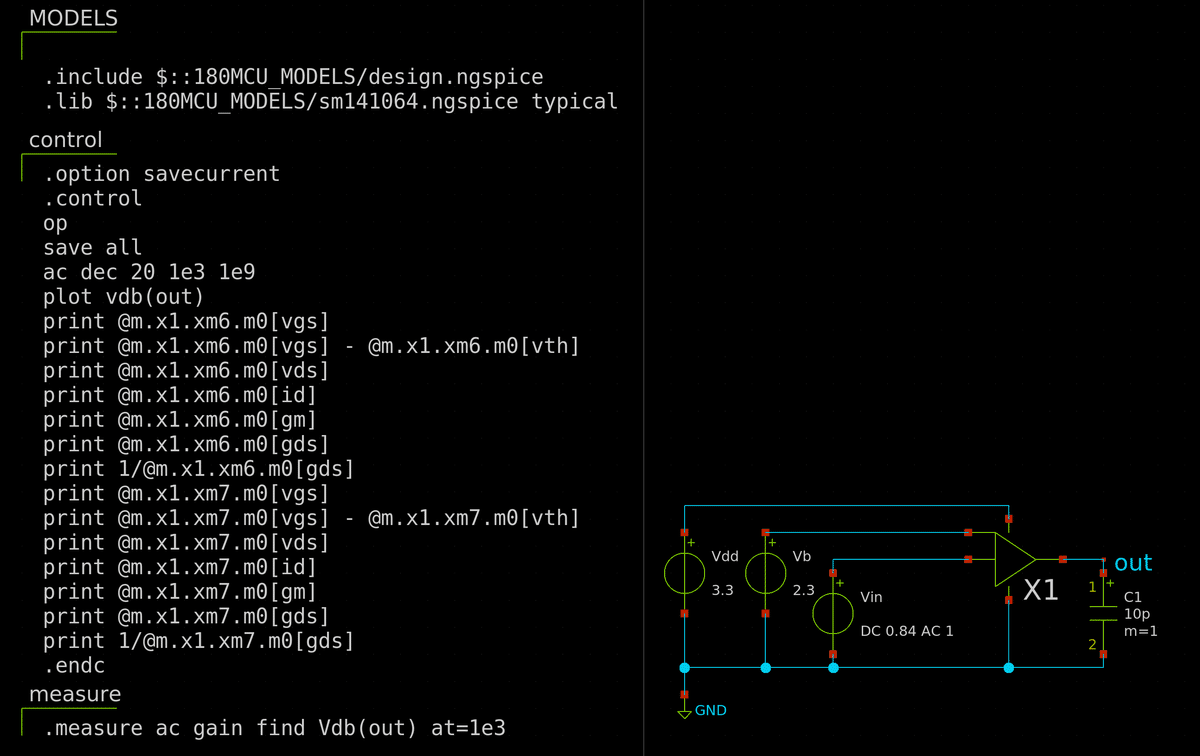
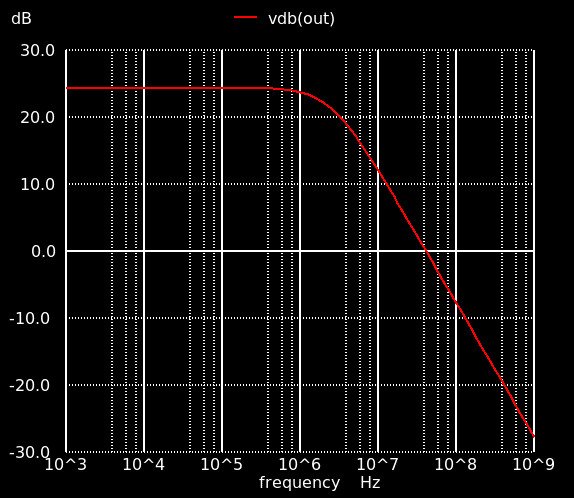
過渡解析を行なってスルーレートも評価しておきます.PWL で立ち下がり信号を入力し,出力信号を評価します.スルーレート 25 V/μs ぐらい,0 V から 3.3 V まで立ち上がるのにかかる時間は 150 nsぐらい.

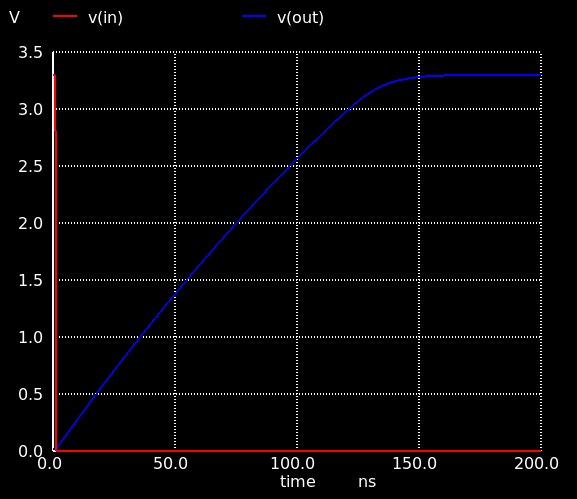
4.2段増幅
ちょっと利得が足りない気もしますが,差動増幅段とソース接地増幅段を接続して利得がどのぐらい出るか確認します.
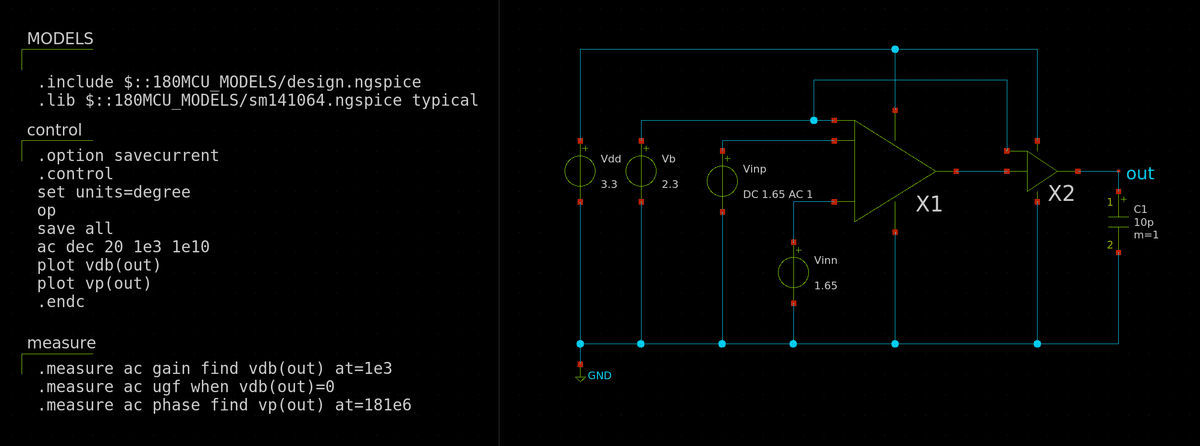
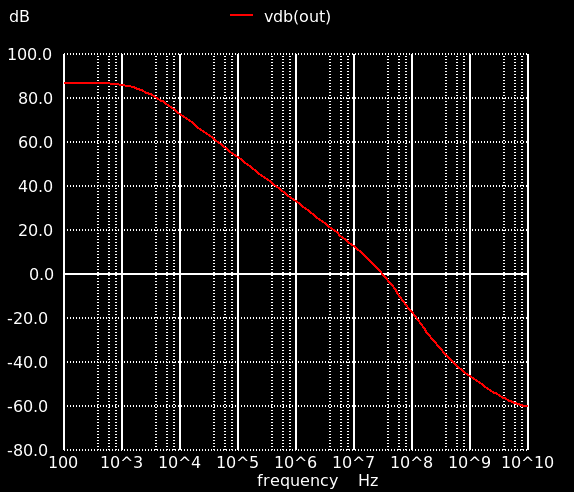
まず利得を見ます.直流利得は54 dB.60 dBに 6 dBほど足りませんがひとまずこれでよしとしましょう.単位利得周波数は .measure で取得して,181 MHzです.
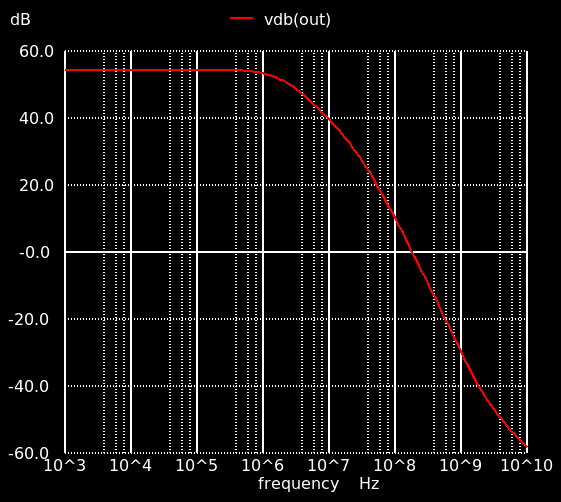
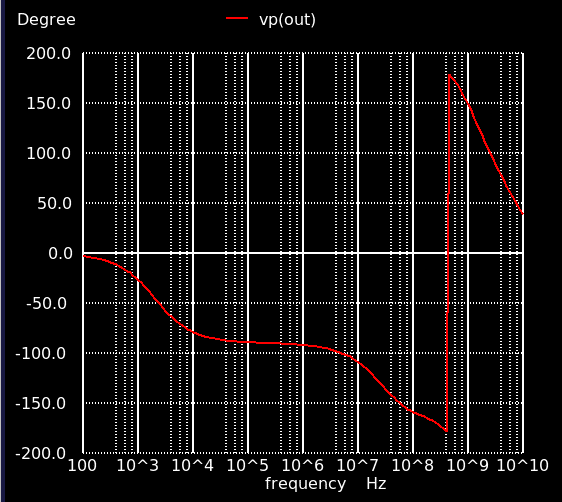
位相曲線を見てみると,単位利得周波数で位相がほぼ180度回っています..measure で取得すると,位相は3.4度.これはほぼ不安定と言っていいので,よろしくありません.
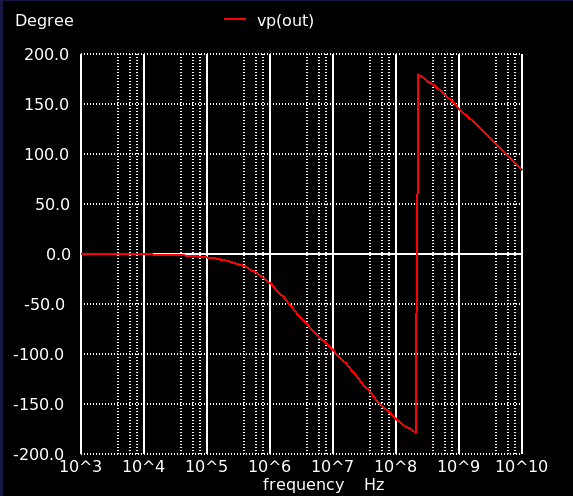
5.位相補償
位相余裕がちょっとまずい数字になっているので,これを60度程度にするために位相補償をかけます.利得曲線・位相曲線から読み取れることは,単位利得周波数より低い位置に第2極がきており,そのため利得が0 dB になる前に位相が回ってしまっている,ということ.というわけで第1極と第2極を分離 (pole splitting) して第2極より先に利得を 0 dB に落とします.
※ 極とか零点が何なのかをここで解説すると長くなるので,分からない人は教科書を読んでください…
5.1 ポールスプリッティング
差動増幅段の出力ノードの時定数を大きくすることで第1極を思いっきり下げます.そのためには容量を追加すればいいのですが,下図のようにソース接地増幅段の入出力をつなぐ形で位相補償容量 Cc を挿入します.容量 Cc はミラー効果によって差動増幅段からは $${(1+A)C_c}$$ に見えます.今,ソース接地増幅段の利得は 24.4 dB (17倍) ですので,$${C_c}$$ は差動増幅段から見れば18倍に見え,第1極を大きく低周波側に下げることができます.
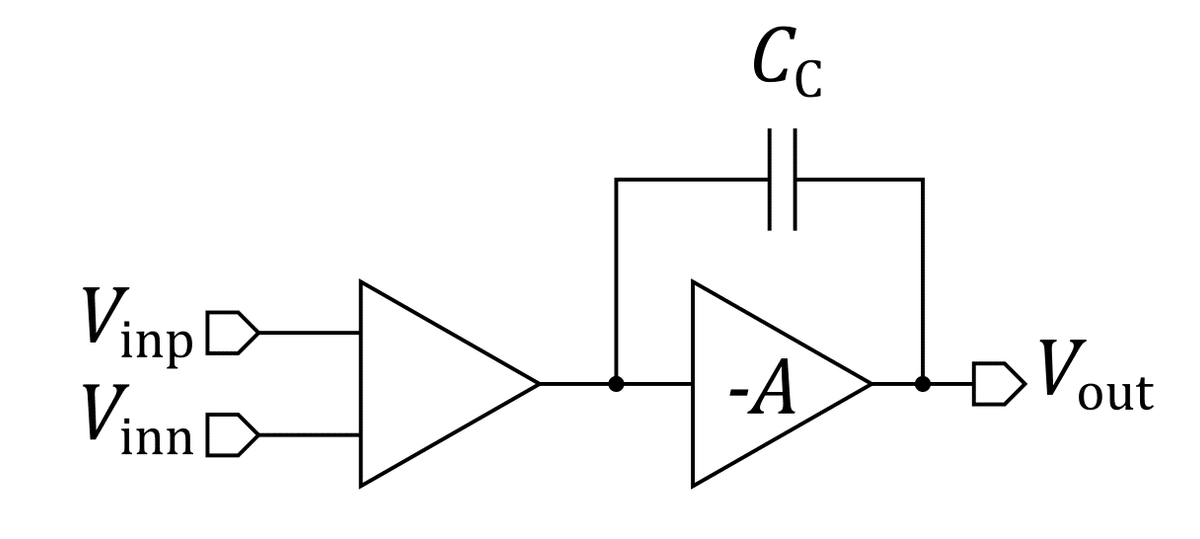
本来は pole-zero 解析で極・零点の位置を確認しながら決めるのですが,ngspice の pole-zero 解析がうまくいきません (原因不明).ということでしかたなく適当な値で設計することにします.適当に 1 pF にしてみましょう.
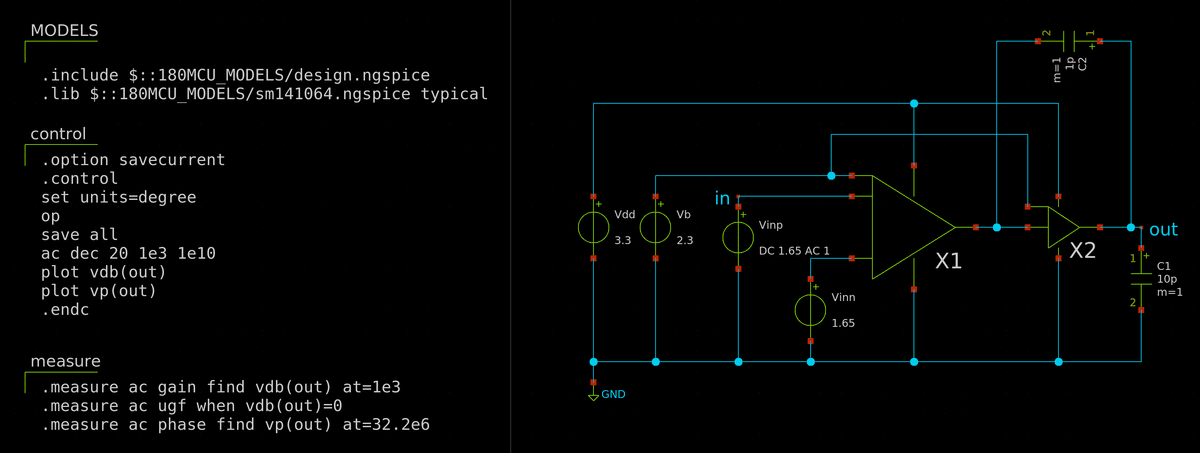
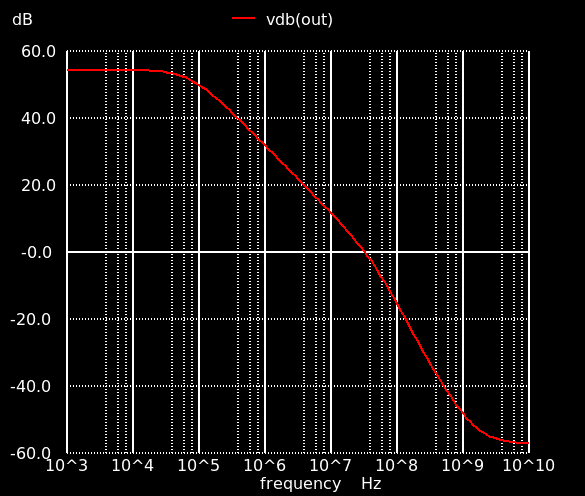
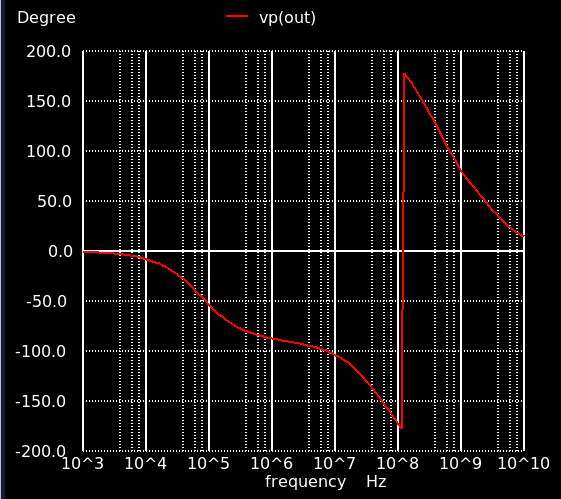
単位利得周波数は 32 MHz とほぼ一桁下がり,位相余裕は50度になりました.容量Cc を増やせば位相余裕60度以上にもできますが,それではよい過渡応答は得られません.Cc を挿入したことで不安定零点が発生しているからです.これを何とかする必要があります.
5.2 位相補償抵抗
説明をいろいろと端折りますが,零点の位置を制御するために直列に抵抗を挿入します.
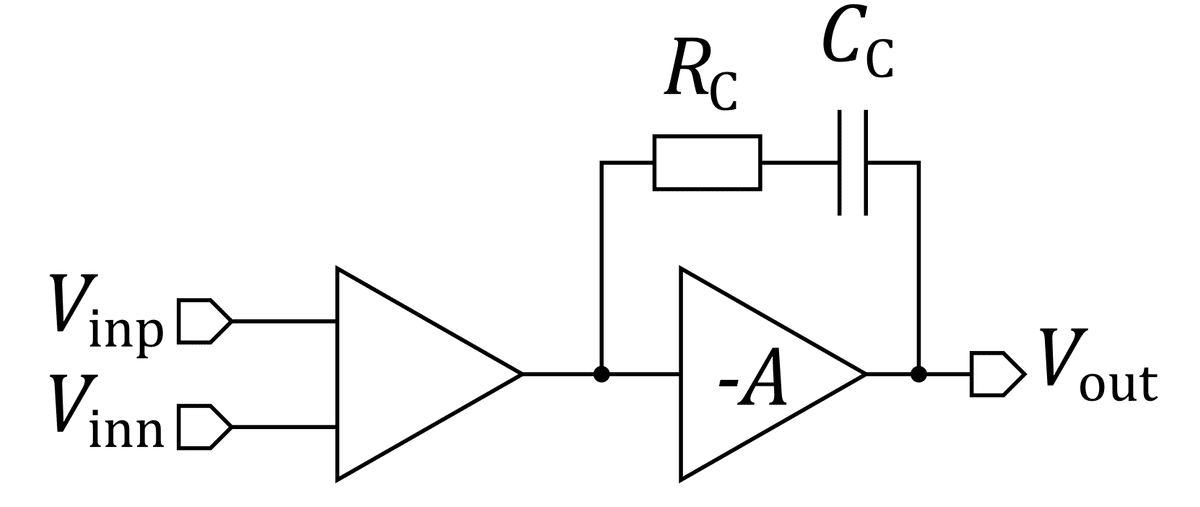
そうすると,伝達関数は3つの極と1つの零点をもつ
$$
\frac{V_{out}}{V_{in}} = A\frac{(1 - s/\omega_z)}{(1 - s/\omega_{p1})(1 - s/\omega_{p2})(1 - s/\omega_{p3})}
$$
となり,極と零点の周波数は近似的に
$$
\omega_{p1}\simeq -\frac{1}{g_{m7}R_6\times R_4C_c},~~ \omega_{p2}\simeq -\frac{g_{m7}}{C_L},~~ \omega_{p3}\simeq-\frac{1}{R_c C_2},~~ \omega_{z}\simeq\frac{1}{C_c(1/g_{m7} - R_c)}
$$
となります.R6 とか R4とか C2 とかはトランジスタの抵抗とか容量です.近似なので適当に書いています.重要なのは零点 $\omega_z$ が右半平面に存在しうること,その位置を Rc によって制御することができる,という点です.不安定零点 (右半平面にある零点) をなくすには大きく2つの方針があり,
零点を無限遠点に飛ばす.つまり $${1/g_{m7} - R_c = 0}$$ より $${g_{m7}R_c = 1}$$にする.(+第2極を単位利得周波数の2倍以上にもっていく)
零点と第2極をぶつけて消す.つまり $${-C_L = C_c(1 - g_{m7}R_c)}$$ より $${g_{m7}R_c = \frac{C_c + C_L}{C_c}}$$ にする.
の2つ.ということで,$${R_c}$$ は適当な大きさかつ $${g_{m7}R_c}$$ が一定になることが求められます.ばらつきなどで $${g_{m7}}$$ が変わるかも知れないということを考えると,固定抵抗ではまずそうな気がします.
5.3 バイアスレプリカ
$${g_{m7}}$$ に連動して値が変わる抵抗とかそんな都合のいいものが作れるのか,という感じですが,これはMOSトランジスタの線形領域を使って作ります.回路図は下図.
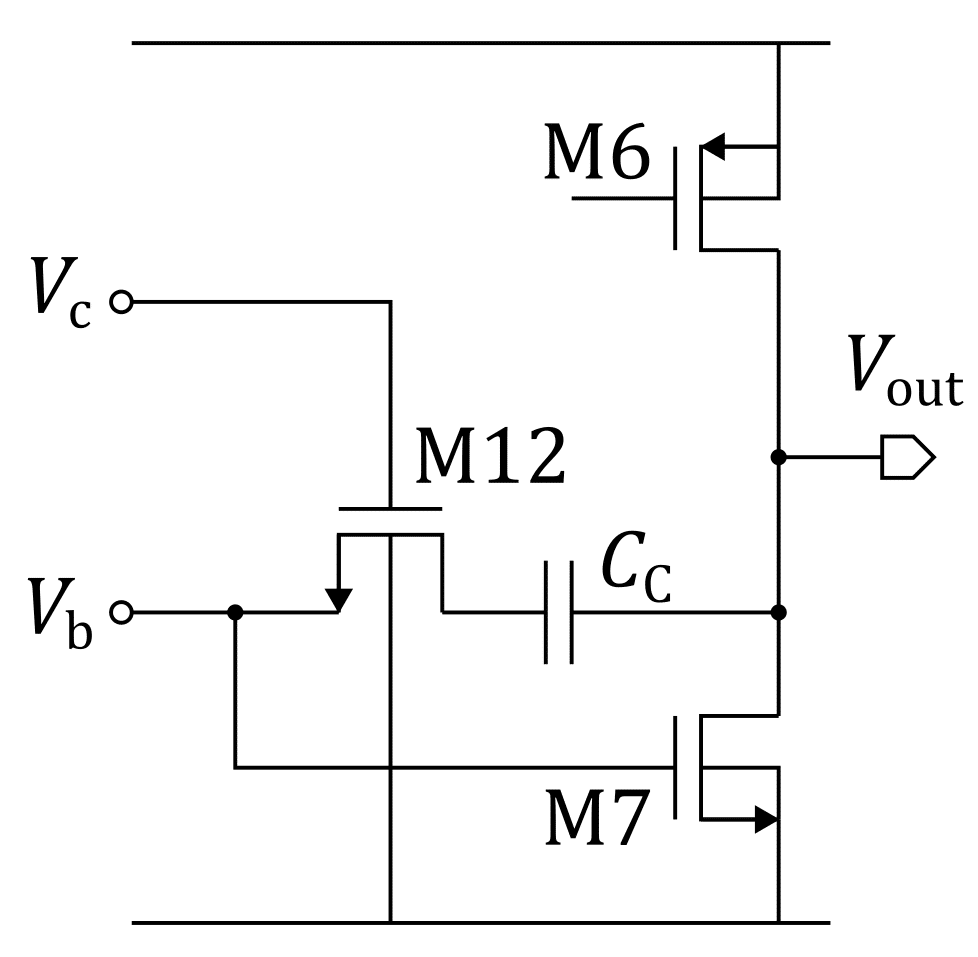
M12 の抵抗値は線形領域の電流の式から
$$
R_c = r_{ds12} = \frac{1}{\mu C_{ox}(W/L)_{12}(V_{gs12} - V_{th})}
$$
一方で M7 の $${g_m}$$ は
$$
g_{m7} = \mu C_{ox}(W/L)_7(V_{gs7} - V_{th})
$$
ということは
$$
g_{m7}R_c = \frac{(W/L)_7(V_{gs7} - V_{th})}{(W/L)_{12}(V_{gs12} - V_{th})}
$$
なので,M7 と M12 のオーバードライブ電圧を一定の比に保てば $${g_{m7}R_c}$$ も一定になることが分かります.$${V_{gs7} = V_b}$$,$${V_{gs12} = V_c - V_b}$$ ですから,$${V_c = 2V_b}$$ となるように $${V_c}$$ を調整すればよいわけです.この $${V_c}$$ を作るのがバイアスレプリカ回路です.
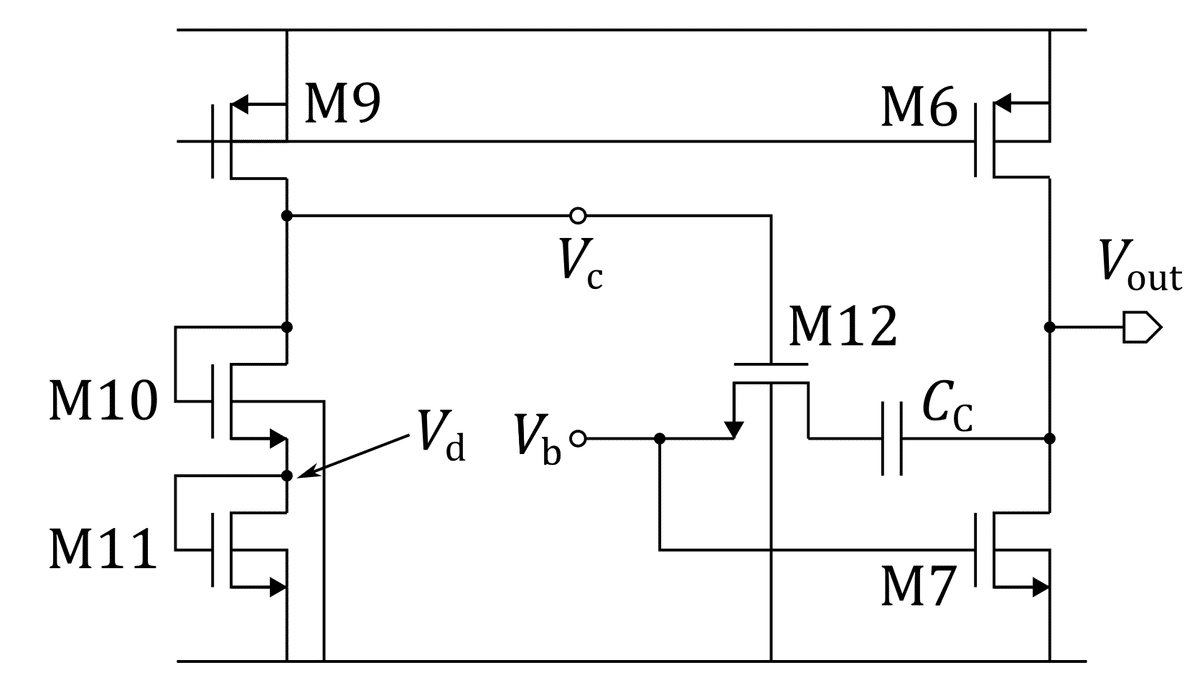
この回路は M6 と M9 でカレントミラーを構成し,M7 に流れる電流と M9 に流れる電流が連動するようにします.M6 は負荷を駆動するために大電流を流すため,そのまま電流をコピーすると無駄に消費電力が増えてしまいます.無駄な電力を使わないように M9 は M6 よりも十分小さくしておきましょう.ここで M9 に流れる電流は M11 に流れる電流に等しいわけですから,$${W_6 : W_9 = W_7 : W_{11}}$$ にしておけば,M11 の $${V_{gs}}$$ つまり $${V_d}$$ は $${V_b}$$ に等しくなります.その上に同じサイズの M10 をつなぐと,同じ電流が流れるので $${V_{gs10} = V_d = V_b}$$ となり,$${V_c = 2V_d = 2V_b}$$ が達成できます.
ということで回路図は下のようになります.
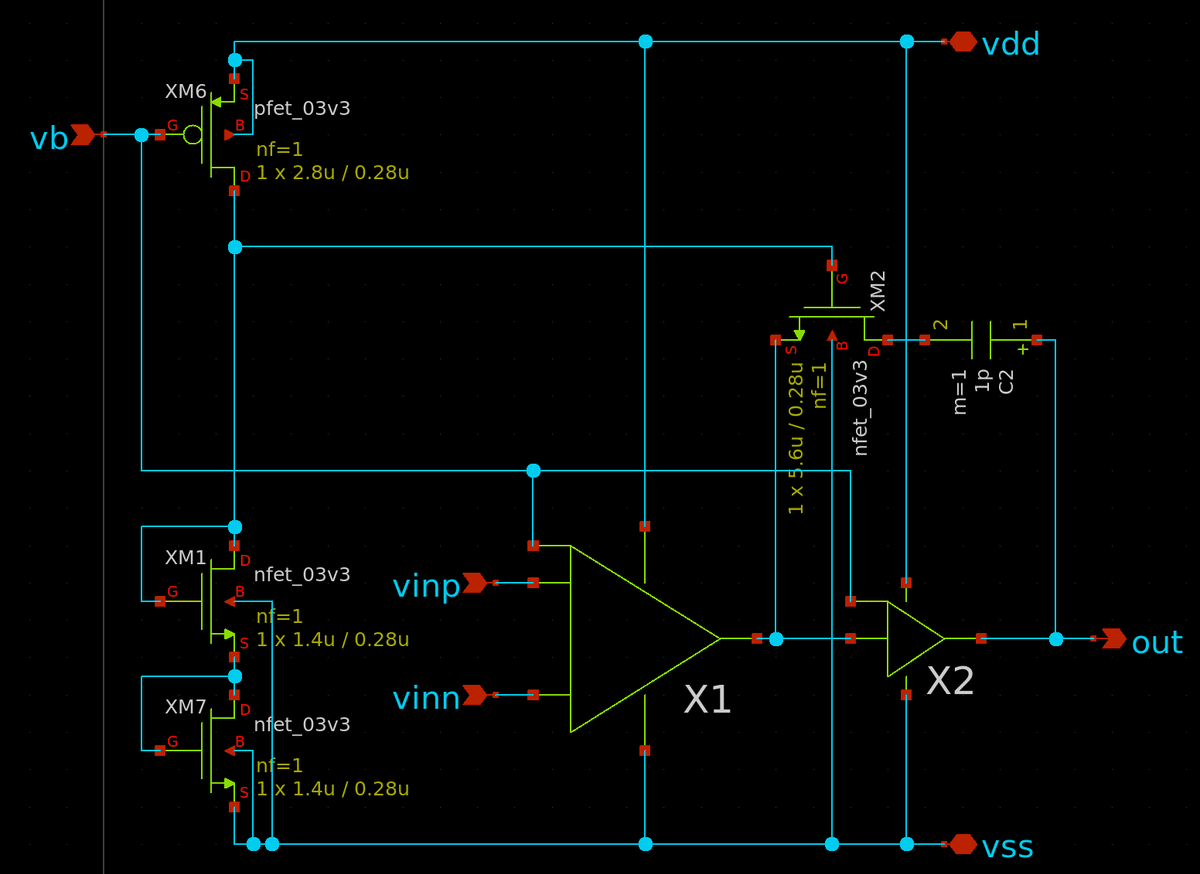
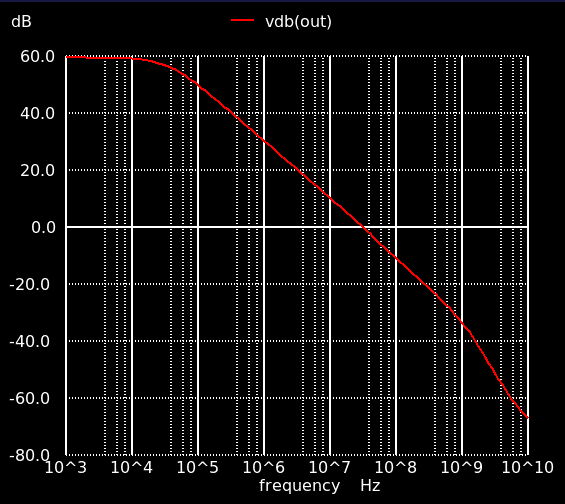
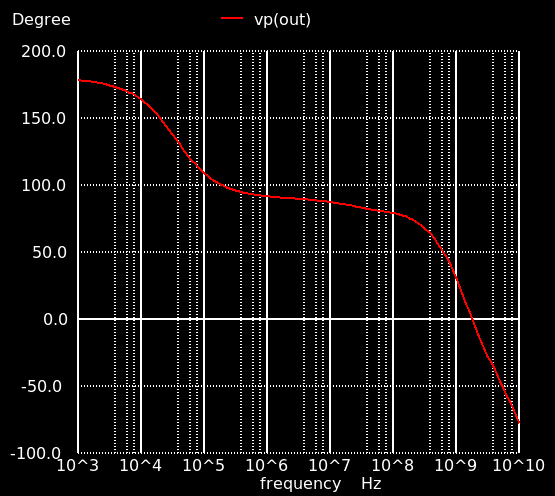
動かしてみるとl (2stage_pc_ac.sch),特性は下の通り.利得は54.5 dB,単位利得周波数 33.1 MHz,位相余裕は 68度.まぁこんなところでしょうか.
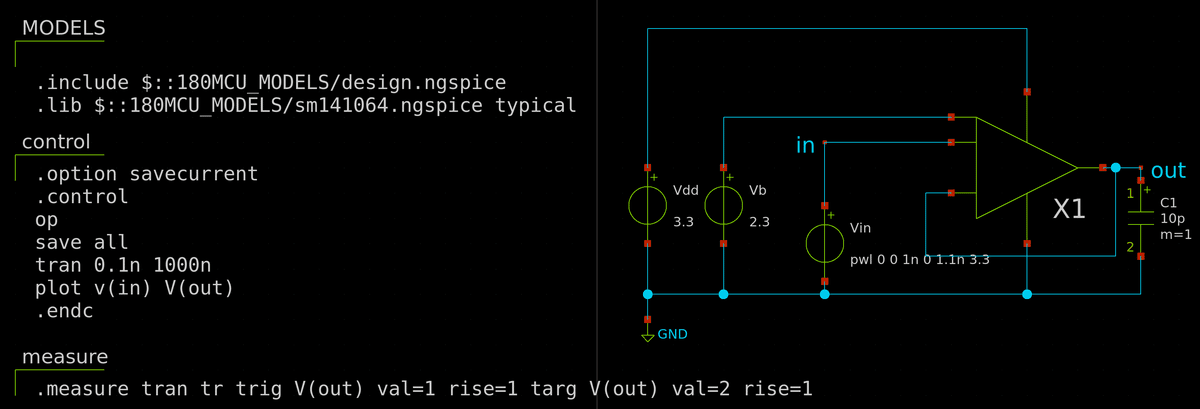
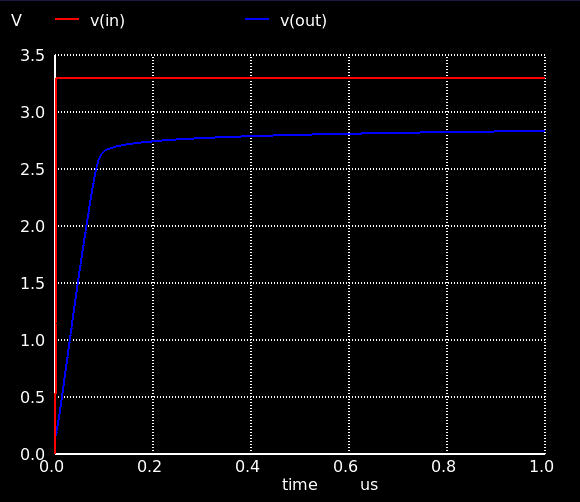
過渡応答も見ておきましょう.ボルテージフォロワの形にして評価します.スルーレートは 29 V/μs.ただし電源電圧一杯に出力を振り切る (rail-to-rail) 動作はできません.
6.完成,各種性能評価
あとは pMOSカレントミラーのゲート電圧を理想電圧源で固定していますので,これを電流源 + pMOS (M8) にします.これはただのカレントミラーなので適当に調整しましょう.特に大きいトランジスタを使う意味はないので,バイアスレプリカと同じサイズにしておきます.
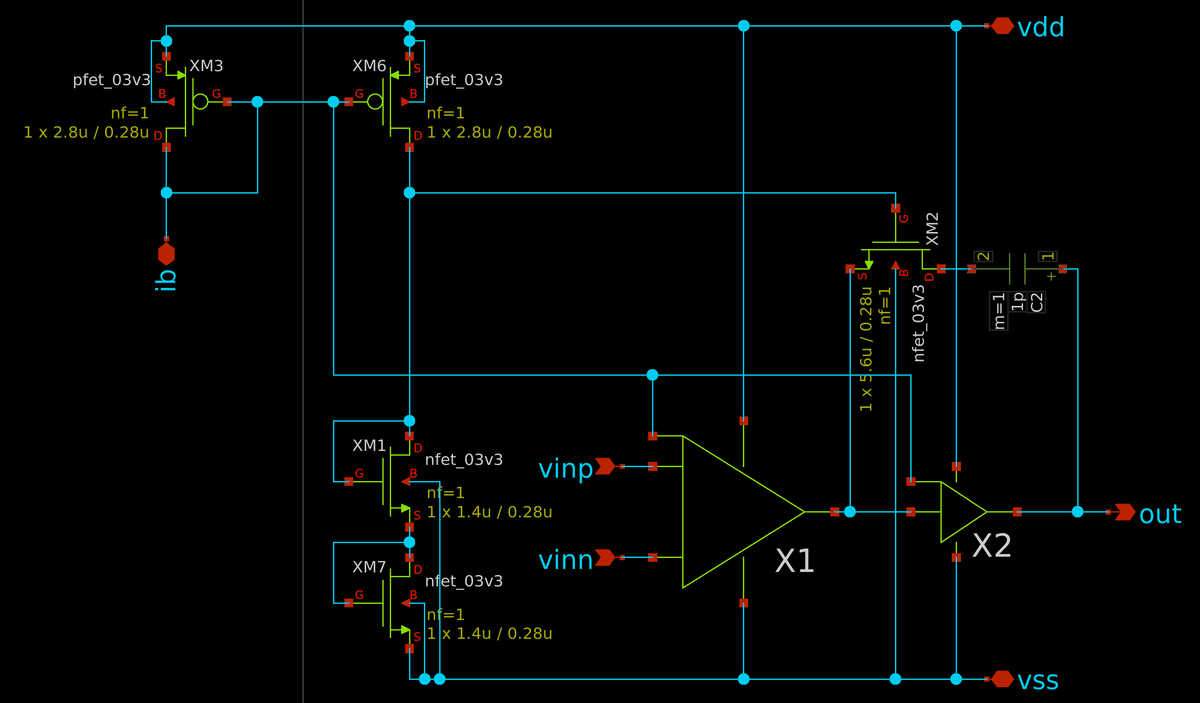
6.1 オープンループ特性
とりあえず利得と位相を確認しておきます.下図の回路ですが,Vinp,Vinn の与え方が変わっていることに注意してください.これまでは Vinn は固定電圧を与えていましたが,ここから先は出力電圧からバイアスを RCローパスフィルタで抜き出してきて Vinn に与えます.
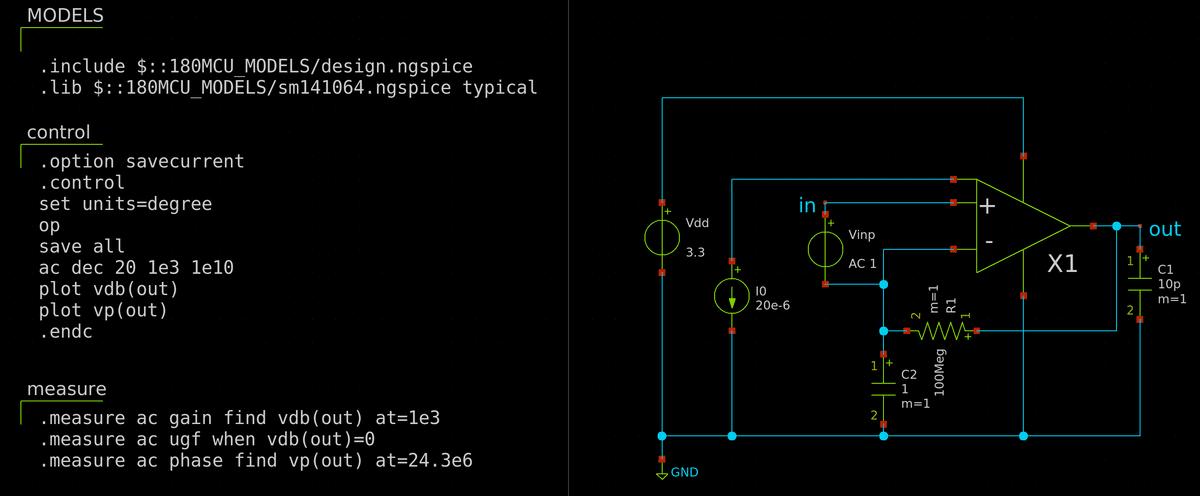
カレントミラーのバイアスが微妙に変わっているのでちょっと特性は変わっていますが,利得 53.7 dB,単位利得周波数 24.3 dB,位相余裕 67度.消費電流は 0.55 mA なので消費電力は 1.8 mW.
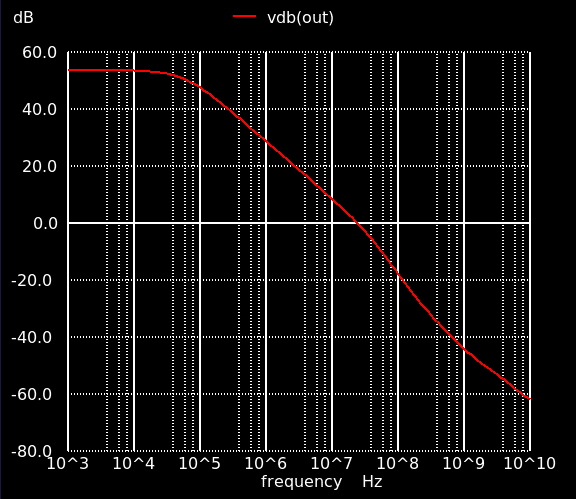
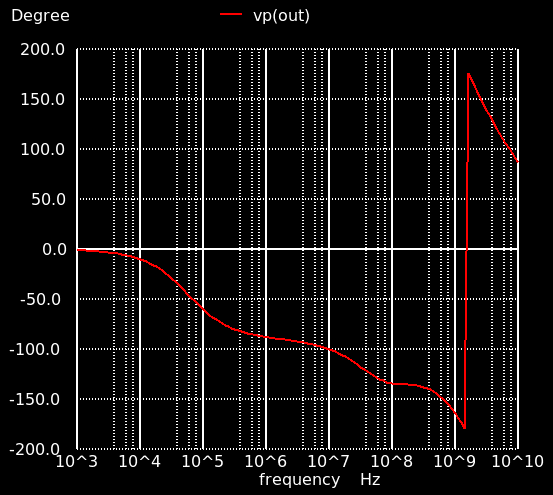
6.2 CMRR
同相信号除去比 CMRR (Common-Mode Rejection Ratio) は差動利得と同相利得の比です.オペアンプは入力端子間の差だけを増幅するのが理想なので,同相信号に対してはまったく反応しない (利得 0倍,$${-\infty}$$ dB) ことが理想です.が,実際には同相信号もある程度は増幅してしまうので,その度合いを表すのが CMRR です.差動利得を $${A_D}$$,同相利得を $${A_C}$$ として
$$
\mathrm{CMRR} = 20\log\left(\frac{A_D}{A_C}\right)
$$
で定義されます.理想値はもちろん $${-\infty}$$ dB.評価回路は以下です.
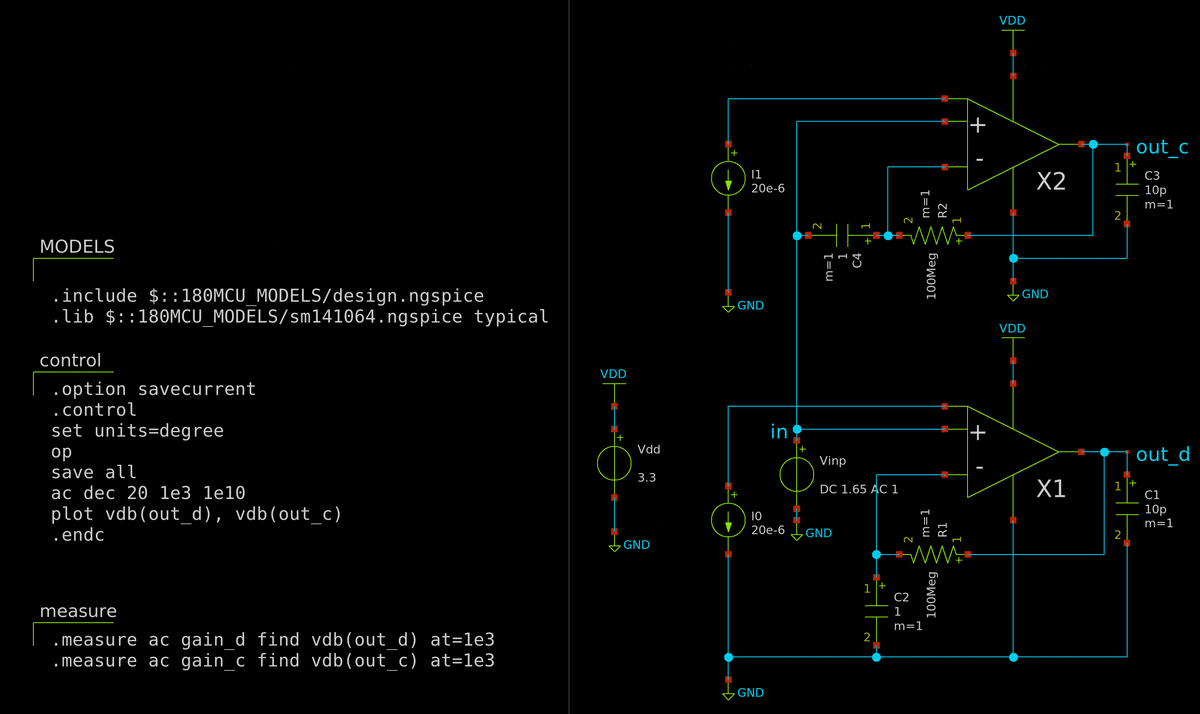
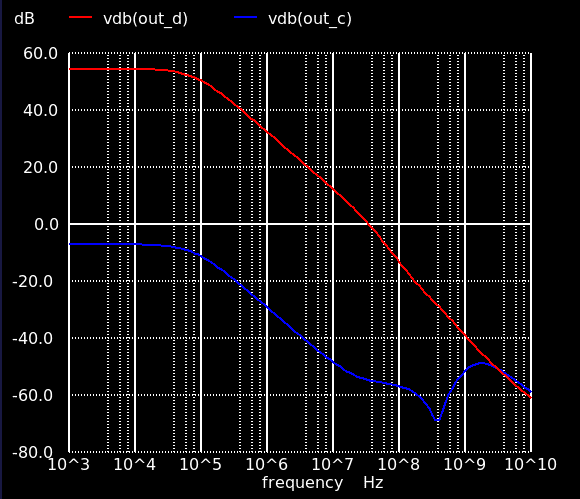
同相利得 (青線) はさすがに 0 dB は超えませんが,そこそこ大きい値になっており CMRR は 61 dB.そんなにいい値ではありません.これは主に差動増幅段のテール電流源が弱い (出力抵抗が小さい) ことなどが原因です.
6.3 PSRR
6.4 入力換算雑音
6.5 スルーレート
6.6 直流特性
6.7 コーナー解析
コーナー解析もやってみます.トランジスタはここまで typical (tt) でやっていますが,これを ff,ss,sf,fs に変えます.それぞれ別のファイルにする必要があります (たぶん).control に追加された wrdata は結果をテキストファイルに保存するコマンドです.実行すると,~/.xschem/simulations/ の下に保存されます.
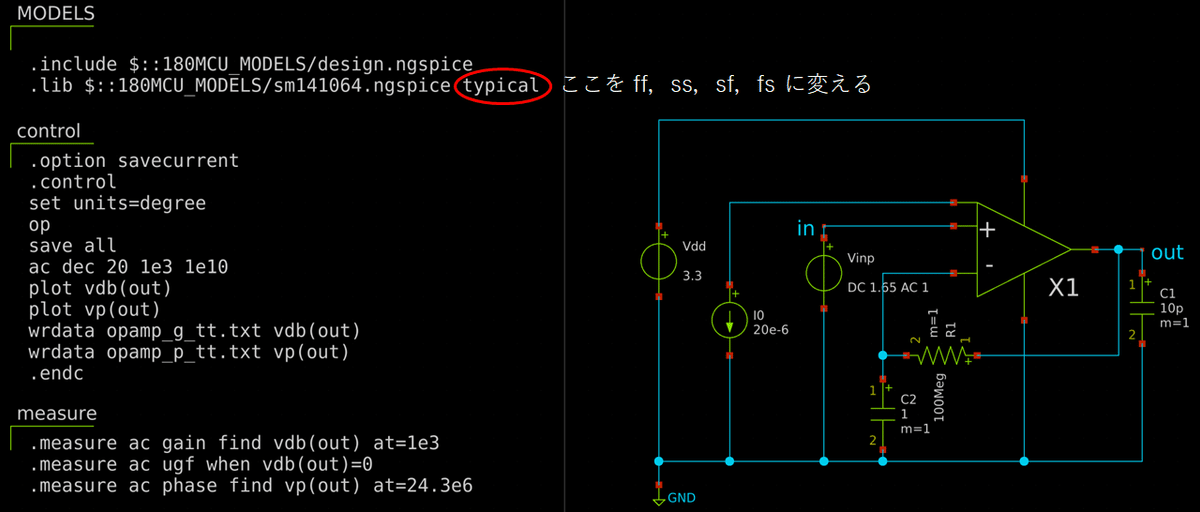
それぞれを解析すると,以下のようになります.グラフを重ねて表示するために,wrdata で書き出したデータを gnuplot でプロットしています.
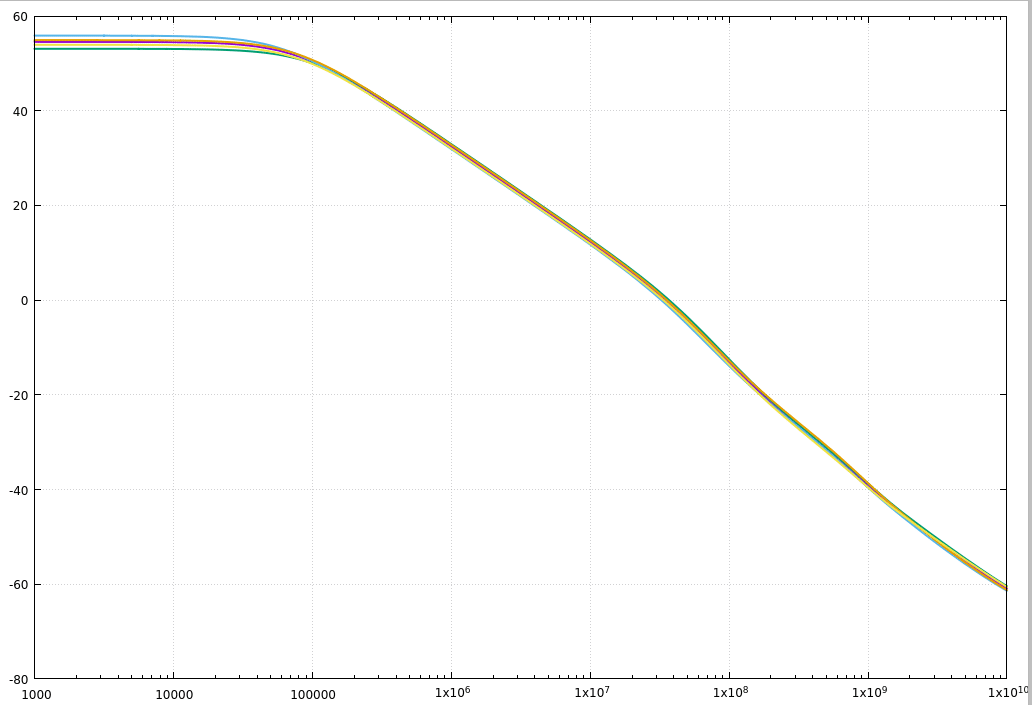
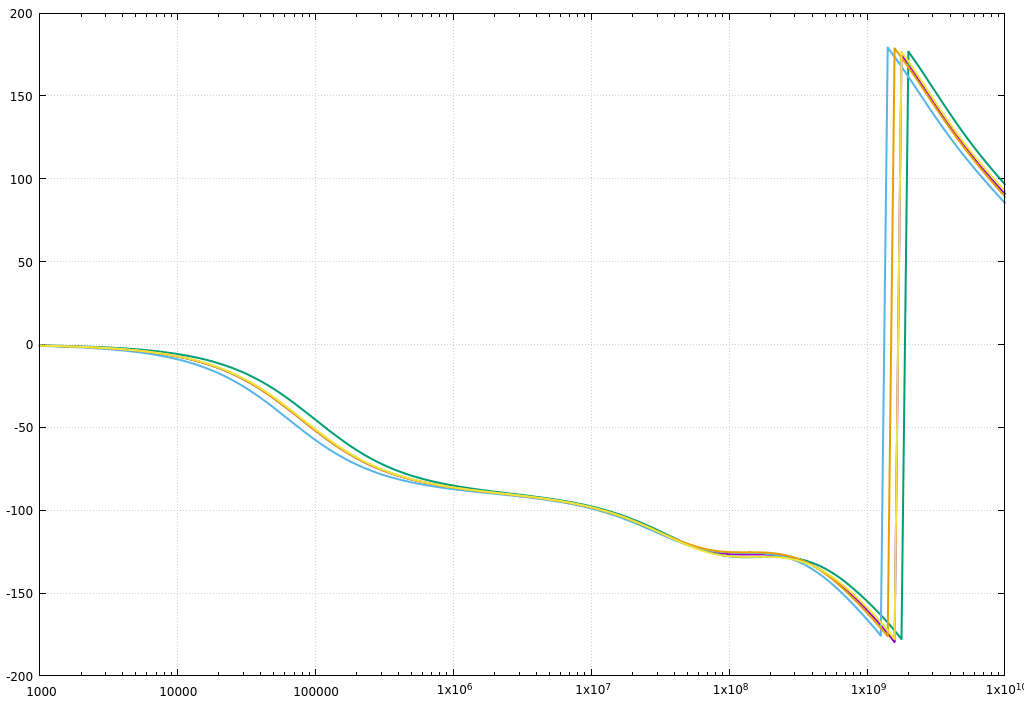
そんなに特性変わらないんだなと思うかも知れませんが,これはカレントミラーの基準電流源を理想電流源にしているためです.逆に言うと,ばらつかない基準電流源があれば,プロセスばらつきの影響はかなり抑制できるということでもあります.
他,電源電圧 (V),温度 (T) も変えて評価しましょう.温度は .temp で変えられます (opamp_ac_temp.sch).
7.改良
ちょっと利得がいまいちなので,改良します.安直なのはチャネル長 L を増やすことです.最初にトランジスタの特性を確認した通り,L を2倍にすれば出力抵抗が上がり,intrinsic gain が一気に上がります.オペアンプの設計は基本的に W/L の比に基づいていますので,W/L が同じになるように W も2倍にすれば,そのままでだいたい動きます.ただし周波数特性は変わるので,位相補償は調整する必要があるかも知れません.
とりあえず L も W も2倍にします.
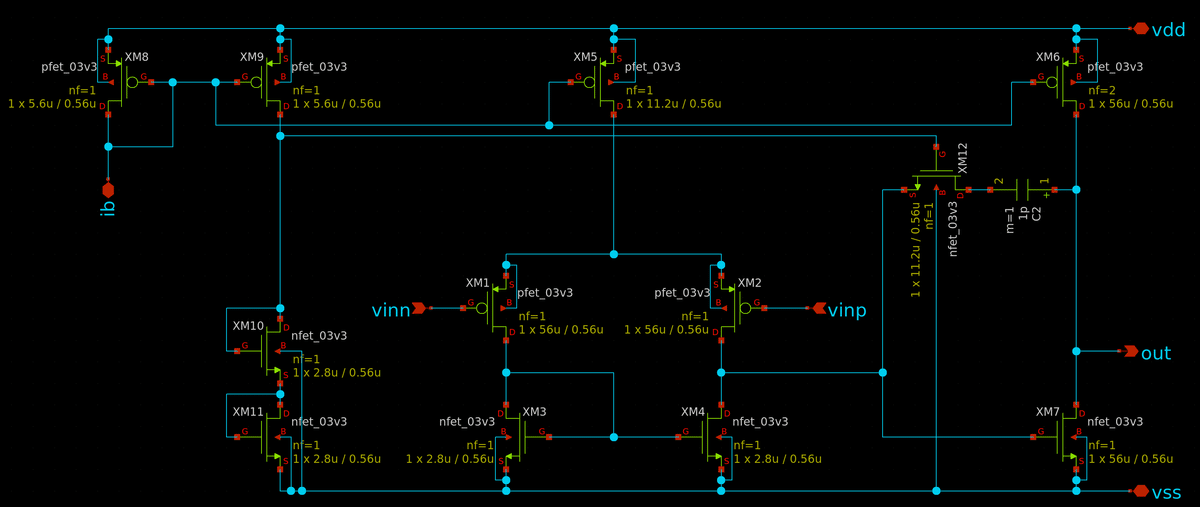
これをシミュレーションすると,利得は一気に 86 dB.単位利得周波数31 MHzで位相余裕は 45度になります.位相補償は調整の必要がありますが,直流利得 86 dB (20000倍) はなかなかの性能です.