【ダダサバイバー攻略】ラッキーイースターエッグイベント ベイズの定理を用いた押し引きの検討(試案)
1 はじめに
「ダダサバイバー」にて開催中のイベント「ラッキーイースターエッグ」,皆様どのように取り組まれていますでしょうか。かく言う私はそもそもダダサバイバー自体プレイしていないのですが,ひょんなことから本イベントの内容を教えられ,朝5時に初めてのnoteである本稿を執筆しています。
本イベントは,完全な運ゲーではなく,何個目までボックスを開けるか,何個目まで来たら爆弾リスクを考慮して撤退するか,という押し引きの判断を伴う点が特徴的で,多少の面白さとそれを凌駕するイライラの原因となっているかと思います。
本稿では,「どうせなら,確率的に割の良い方法に従って,損なく,かつ,無用なストレスなくイベントを進めたい」という観点から,ベイズの定理を用いて数学的に判断基準を考えてみることとしました。
もっとも,なにぶん筆者はそこらの文系出身者であり,検討に用いた知識はほぼ趣味でかじった程度のもの,本稿もまた,それを試す頭の体操的な取り組みにすぎません。多分に計算ミス等を含むものと思いますので,本稿をもとに各位が行われた判断について一切の責任を負わない旨を留保するとともに,お気づきの点があれば後学のためコメント等を頂けますと幸甚です。
2 ルール,用語など
ラッキーイースターエッグの基本ルールについては,下記のページを参考としました(以下,「参考ページ①」)。ルール自体の説明は,本稿では割愛します。
また,以下の説明では,エッグポイントを単に「ポイント」又は「点」,イースターエッグを「色卵」,ゴールデンエッグを「金卵」,両者の総称を単に「卵」と呼ぶこととします。
さらに,便宜上,スーパーイースターエッグモードに移行する前のモードを「通常モード」,通常モードで表示される25個のボックス全体を「場」と呼ぶこととします。
3 試算
上述したように,本イベントで最も重要なのは,何個目までボックスを開けるか,何個目まで来たら爆弾リスクを考慮して撤退するか,という押し引きの判断です。確率的にいえば,次のボックスを開けたときに保有している点の期待値が,すでに保有している点より高いのなら,次のボックスを開けるべき,そうでないなら撤退して今保有している点で利確すべき,ということとなるはずです。本試算では,このような視点から期待値を計算していきます。
なお,ゲーム設計の都合から生まれる細かい要素(例えば,純粋な確率の話でいえば,各ラウンド開始時に自動で開いたボックスに,金卵が3つとも含まれる可能性も一応あります。もっとも,流石にそのような現象は生じないように設計されているかと思います)については,計算が複雑になるため,今回は考慮に入れていません。ご了承ください。
(1)通常モードのポイント期待値
ア 次に爆弾を開けてしまう確率と,その場合に失うポイント
ある時点で,すでに開いた卵の個数をn個とします(卵以外,即ち爆弾を開けばそのラウンドは終わってしまいますから,すでに開いた「ボックス」の個数,と考えてもよいです)。残った場には必ず爆弾3個が含まれているはずなので,n+1個目を開こうとしたときに爆弾を開いてしまう確率qは,$${q=3/(25-n)}$$ですね。
これをまとめたものが以下(表1)です。$${3/25=12%}$$,$${3/24=1/8=12.5%}$$…と,徐々に爆弾を開くリスクが上がることがわかります。

イ 次に卵を開ける確率と,その場合に得られるポイント
つづいて,参考ページ①に掲載されている,開けた卵の総個数ごとの得点表をもとに,以下の表2を作ります。r列のn行目の値をn+1行目の値から引いて,次に卵を開いたときに得られるポイントをs列に書いただけなので,何のことはありません。なお,赤字部分は参考ページ①に記載がなかったため,便宜上推定値を用いています。

そして,n+1個目を開こうとしたときに卵を開く確率は,爆弾を開く確率qの余事象にあたるので,$${1-q}$$と表せます。
ウ 期待値
これらをまとめると,n個の卵を開いた状態で,n+1個目を開くときに加わるポイントの期待値αは,
$${α=s*(1-q)-r*q}$$
になるかと思います(表3)。この値が負になる時点で,撤退したほうが良いとの判断となるわけです。
各種攻略サイトなどで,320ポイント取れたあたりで止めておくのが無難,といった意見を見かけましたが,ここまでの計算からしても同様の判断が得られます。
仮にこのイベントが,「25個中3個ある爆弾を避けながら色卵を引き,程よいところで撤退してポイントを獲得する」だけの内容であれば,この計算で足ります。しかしながら,以下のとおりスーパーイースターエッグモードを考慮に入れる必要があるため,計算はここまで単純ではありません。

(2)スーパーイースターエッグモードのポイント期待値
ア スーパーイースターエッグモードに行けた後の得点期待値
スーパーイースターエッグに行けたことを前提に(何割の確率で同モードに行けるかどうかは慮外にして)得られるポイントの期待値を考えます。これは簡単でしょう。参考ページ①のとおり,同モードの結果として得られるポイントは24000,10000,5000,2000の4種類で,かつ,金・桃・青・緑卵の個数は3つずつですから,$${1/4*(24000+10000+5000+2000)=10250}$$となります。
イ あるラウンドで,場に金卵がx個ある確率Bx
ご存じのとおり,すべてのラウンドで場に金卵が3個あるとは限りません。0~2個しか無い場を必死で開けて爆弾を食らう,ということもざらにあるのが,本イベントの無情なところです。
ざっと探したのですが,金卵が0~3個の場が,それぞれどのような確率で発生するのかまで考察している攻略サイト等は見当たりませんでした。そこで,さしあたり30ラウンドで統計を取り,各リザルトで表示された金卵の個数を調べたところ,以下のようになりました(表4)。ここからは,この割合を使うこととします。当然,さらに大規模な統計ができれば割合の正確性は上がるでしょう。
また,金卵がx個ある場のことを「x個場」,そのラウンドがx個場である確率を$${Bx}$$と表すことにします。

ウ 事後確率を考慮に入れた検討
ここからが本稿の肝となる部分です。
本イベントの仕様上,決定的に重要なのは「3個場かそれ以外の場かを見極めて,押し引きを決める」ことです。3個場以外は0個場だろうが2個場だろうがスーパーイースターエッグモードに行ける可能性はないという意味で等しくスカでしかないからです。
ここで,例えば,まだ何も始まっていない次のラウンドについて,3個場である確率を予想するなら,表4のとおり17%とするほかありません。一方で,すでに開始し,自動で開いた卵や自分で開いた卵が増えているラウンドについては,ずっと17%のままとはならないはずです。つまり,
ボックスを10個開いたが金卵はなく,全部色卵だった。ここまで来ると,残りの15個のボックスに金卵が3個も隠れているとは考えにくく,せいぜい1,2個しかない(すなわち,このラウンドは3個場ではない)のでは?
自動で5個開いた中に金卵がすでに2個あった。2個場の金卵を2個とも開きつくすのは相当レアだろうから,このラウンドは3個場で,3個のうちの2個に当たったのだと考えるのが自然では?
といったように,すでに開いた卵の内訳によって,場に対する読み方を変える必要があるのです。このラウンドはしょっぱそうだな,といった直感を覚えた経験があるかと思いますが,本稿では,この直感を確率として数値化します。
エ ベイズの定理
そこでベイズの定理を用います。
前提知識も含めて把握されたい場合は,BellCurveが分かりやすくまとまっていると思いますので,本稿でも参照させていただきます(以下,「参考ページ②」)。
ここでは,参考ページ②のうち以下の式を用います。

本試算でいえば,
$${P(Bx/Am,n) }$$:n個開いた中に金卵がm個含まれていたとき,そのラウンドがx個場である確率
を求めるため,
$${P(Bx)}$$:そのラウンドがx個場である事前確率(上述)
$${P(Am,n/Bx) }$$:そのラウンドがx個場のとき,n個開いた中に金卵がm個含まれている確率をこの式に入れていきます。
また,右辺の分母にあるΣ計算では,0個場~3個場の場合(j=0,1,2,3の場合)を順番に考えた後足し合わせることとなります。
$${P(Bx)}$$については,表4より,x=0,1,2,3の場合の各値が分かっていますので,計算が必要なのは$${P(Am,n/Bx) }$$です。
例としてx=2,n=5,m=1のときの確率を考えてみます。
高校数学で習う組み合わせの式を使えば,
$${P(A_{5,25}/B_2) ={}_2 C_1*{}_{25-2} C_{5-1}/{}_{25} C_5={}_2 C_1*{}_{23} C_{4}/{}_{25} C_5}$$
として求めることができます。
同様に,$${P(A_{m,n}/B_x) ={}_x C_m*{}_{25-x} C_{n-m}/{}_{25} C_n}$$により各x,m,nの場合を計算したものが表5です。0個場ならm=0にしかなりようがないのでどの行も100%となっていることや,各行において,x個場のときの確率を4マス足し合わせると100%になることが確認できます。

表4の$${P(Bx)}$$と,表5の$${P(Am,n/Bx) }$$から,表6のとおり$${P(Bx/Am,n) }$$を求めることができました。

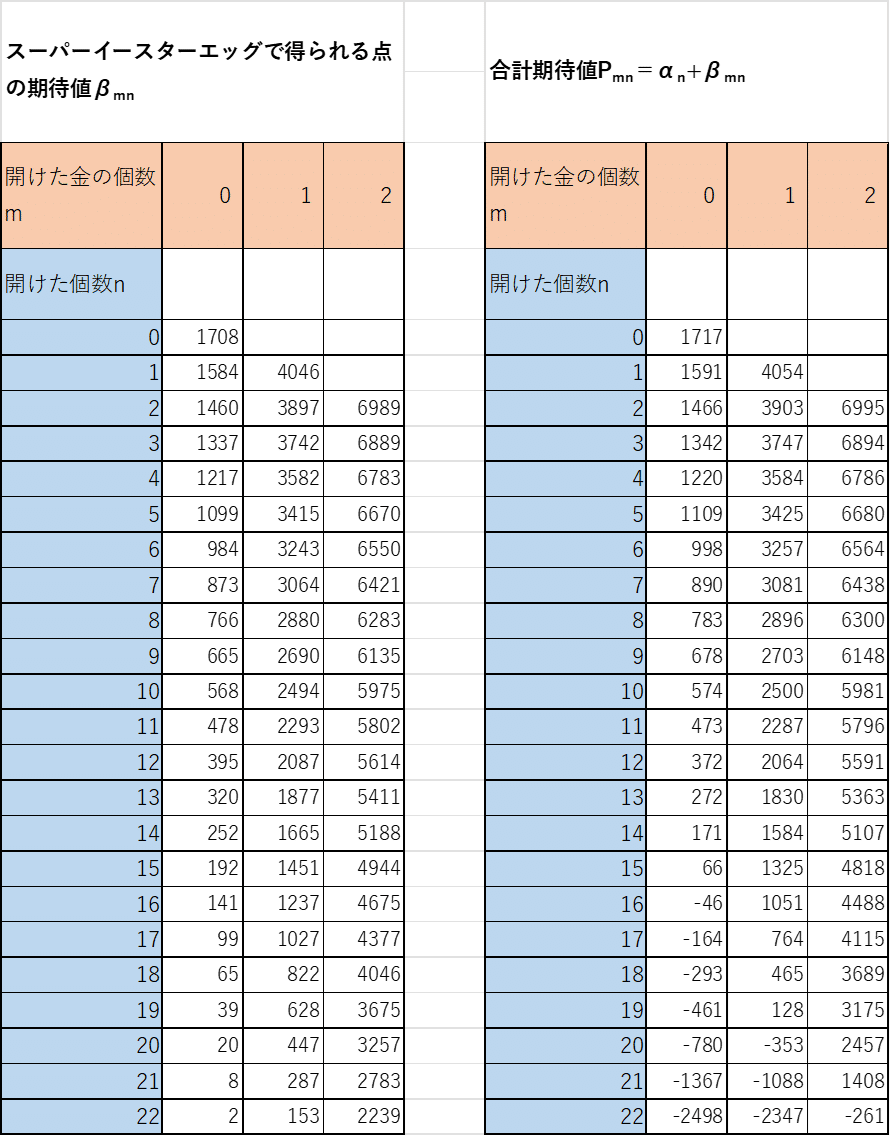
この表のx=3となっている右端4列に,上述の10250をかけたものが,スーパーイースターエッグモードで得られるポイントの期待値βとなります。とはいっても,m=3すなわち既に金卵を3個開いているのであれば,それ以上ボックスを開くかどうかを考える必要はありませんから,実際には右端4列目から2列目までが,押し引きの判断に必要な数値です。
これらの列の各行に10250をかけたものが表7で,さらに,(1)にてまとめた期待値αと合算したものが表8になります。
(3)結論
表8の各値から,表2のrを引いたものが以下の表9です。これが負になっている箇所(赤色セル部分)は,「スーパーイースターエッグモードに行ける可能性,及び行った場合に得られるポイントの期待値まで考慮しても撤退すべき」という判断になります。

以上より,
(0) 開いている金卵が0個のとき…12個まで開く。それでも金卵が0個のままなら,400ポイントをもって撤退する(途中で金卵を開いたら(i)以下へ)
(i) 開いている金卵が1個のとき…17個まで開く。それでも金卵が1個のままなら,950ポイントをもって撤退する(途中で金卵を開いたら(ii)へ)
(ii) 開いている金卵が1個のとき…21個まで開く(事実上,ほぼ全ツッパ)。それでも金卵が2個のままなら,2000ポイントをもって撤退する
というのが押し引きの判断基準となるかと思います。総括すると,スーパーイースターエッグモードにさえ行ければ桁違いのポイントが手に入るため,体感よりも結構押し気味の判断が得策になる,といったところでしょうか。
最後までご覧いただき,ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
