ハバネロ解説(2012年五月祭)
問題。
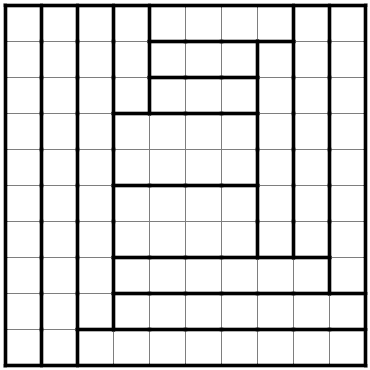
「へやわけ」というパズルです。
・縦横に連続しないように黒マスを配置する。
・白マスは全体でひとつながりになるが、3部屋まっすぐに続かないようにする。
というルールで解けます。
(今回は数字はないので省略します。)
2012年の東京大学五月祭で配布された超難問冊子「ハバネロ」に載っています。
最近、へやわけの黒マス充填に関する理論が多くTwitterで話題になり、
SP1さんがこんな記事を書いていました。
……いが大きいなあ。
過去の話。
時は2012年。
所属する東京大学ペンシルパズル同好会で、
パズル大会を開こうという企画が持ち上がりました。
UTPC(the University of Tokyo Puzzle Championship)です。
私はニコリラウンドの
スリザーリンク、へやわけ、ごきげんななめ
の3種類3問を担当することになりました。
(そういえば作者のところにさやちぃ。の名前がないですね。
知ってる人は知ってると思いますが旧名義で載ってます。)
とはいえ当時の私はパズル大会というものに参加したこともなく
ましてや大会用の問題を作ったことなんてありません。
難易度の加減とかいうものがわからない状態で私は、
とりあえずスリザーリンクとへやわけを2問ずつ送りました。
1問は採用されました。スリザーリンクの2番(6-2)です。
2問はボツにされました。スリザーリンクとへやわけ1問ずつ。
そしてもう1問は、ハバネロにされました。
そう私はこの記事のメインテーマとなるあの問題を
パズル大会の中の1問にするつもりで作っていたらしいです。
今から考えると恐ろしい。
というわけで、さやちぃ。のハバネロデビュー作はこうして生まれました。
(ちなみに、最終的にUTPCに出題した問題は、
ニコリラウンドの6-2、8-1、9-2の3問でした。)
(難易度の加減は今でもわからない…………)
解説
(当然ですが、記事のこの先の部分にはネタバレを含みます。
まだ問題を解いていない方で、まだ自力で解こうという気力がある方は
読まないほうがいいと思います。)
まずはこちらをご覧ください。
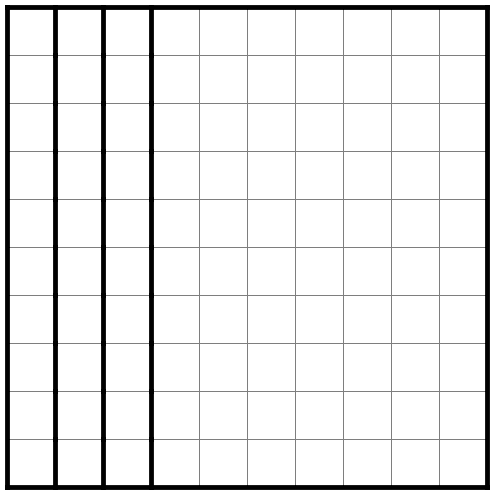
数字もなにもないへやわけに3本の線を引いただけです。
ここに数字を入れていくとなんか入り口になりそう……な気もしますが。
実はこの盤面、すでに破綻しています。
なぜでしょうか。
ある1つの行について、左から4列の黒マスの配置を考えます。
2列目or3列目が黒マスのときは、他の3マスは白マスにすることができます。
2列目と3列目が白マスだと、1列目と4列目はともに黒マスになります。
また、1列目と3列目、2列目と4列目に黒マスを置くと、
その間の白マスが分断されてしまいます。
つまりどの行についても、左から4列の黒マスの配置は、
・2列目だけ
・3列目だけ
・1列目と4列目
の3通りしかありません。
これを上から順に配置していくと、
例えばこうなります。

左下で黒マスが分断されてしまいました。
他の場合でも、
・上辺から下辺まで黒マスがつながる
・上辺からつながった黒マスが左辺につながる
・上辺からつながった黒マスは右(4列目)に行くが、
それと同時に左辺(1列目)から出た黒マスが
下辺または左辺につながる
のどれかが必ず発生し、白マスが分断されてしまいます。
さて、実際の問題では、左のほうはこうなっていました。
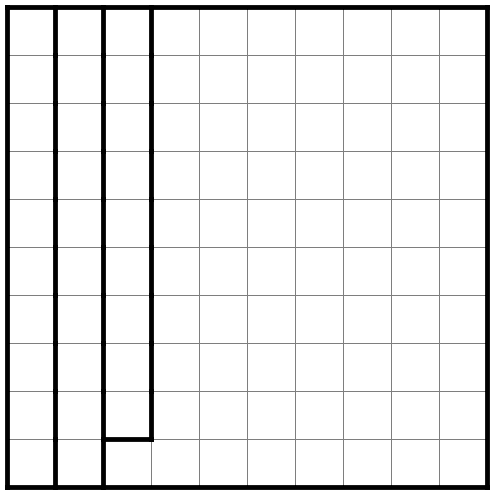
3列目の部屋だけが、下辺まで届いていません。
これが上で書いた破綻を回避するポイントになります。
せっかく形が変わって回避できるのに、
一番下の行で上に書いた3通りの黒マスの配置をしていては、
やはり破綻するはずです。
ただし1〜3列目のうちどれかは黒マスにしなければなりません。
ということは、ここの黒マスの配置は、
1列目は黒マス、2〜4列目は白マスしかありません。

さらに分断回避は続きます。
9行目(下から2行目)は黒マスが左下隅の黒マスとつながるとまた分断します。
したがってこの行の黒マスは3列目になります。
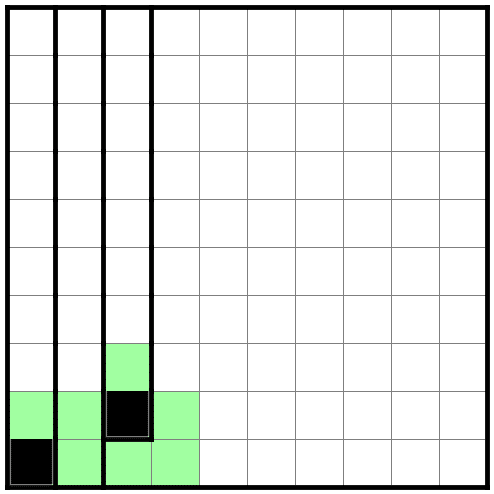
ところで今置いた2個目の黒マス、
今までに書いた内容から考えると必ず左辺か上辺とつながっているはずです。
ということは、ここから黒マスが伸びて下辺や右辺につながってはいけません。
さて、下のほうの部屋を増やしてみます。
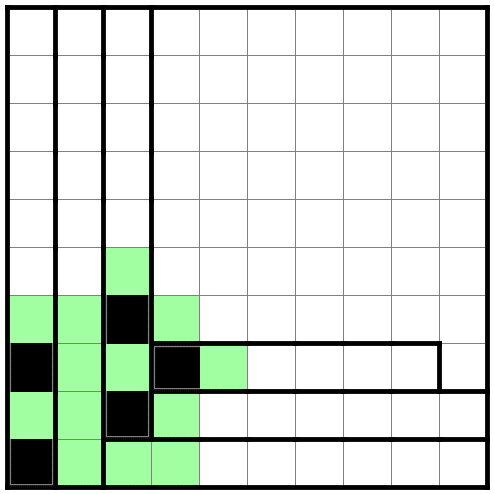
少し進めました。
すでに決まっていた白マス2つから3連禁で8行目の黒マスが決まり、
先に書いた黒マスが左辺か上辺とつながることから7行目も決まります。
さて下のほうの部屋ですが、ここも左と同じ形をしています。
そしてここも一番右で同じ回避をしないと、
下辺または8行4列の黒マス〜下辺または右辺で黒マスがつながり、
白マスが分断してしまいます。
ということは、こうなります。
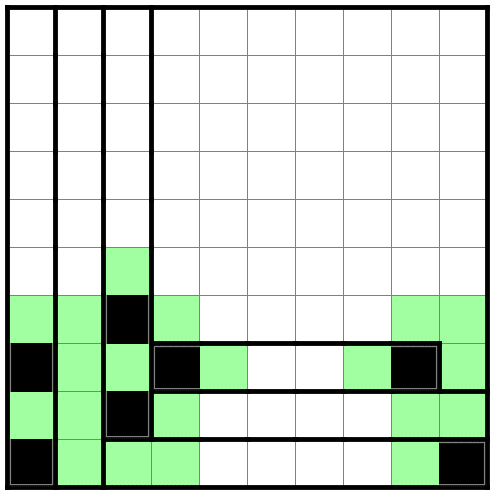
右のほうの部屋も足してみましょう。
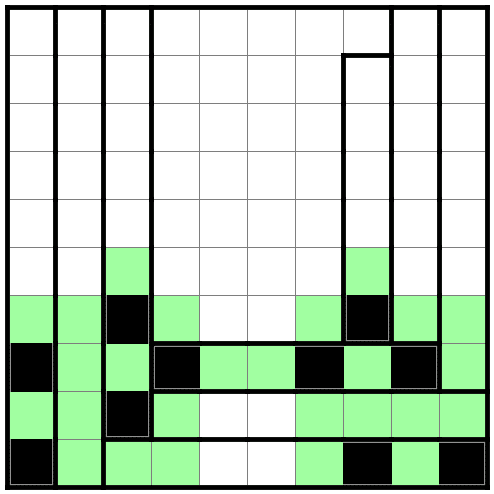
もう、わかりますよね。

さらに他の部屋を書いてしまいます。
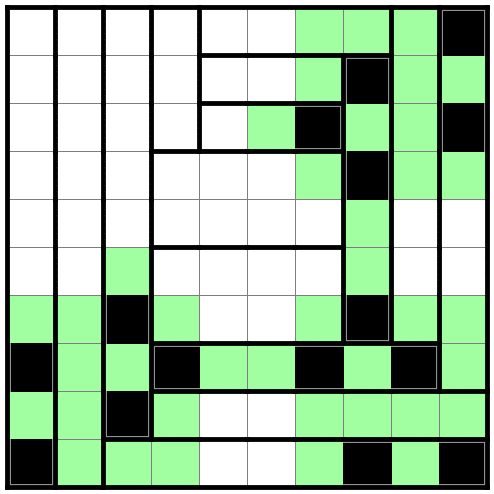
下辺と右辺に2×2の空白ができています。
ここにはそれぞれ2個の黒マスが入りますが、
今までに考えた黒マスのつながりから確定するはずです。
(8行4列の黒マスは下辺と、7行8列の黒マスは右辺とつながらない)

ここまでくれば、あとは単純な分断禁と3連禁で埋まっていきます。

これで完成です。
おわりに
作ってから8年経ったこの問題ですが、
実はいまだに「本当にこの問題は唯一解なのか?」と思うことがあります。
……いや、この記事書いてる今でも自信ないので、
誰かちゃんと確認してください。お願いします。
