
中学1年と2年の文字式の割り算の捉え方のちがい
1 中学1年と2年で学習する文字式の割り算
中学1年生では、$${6x÷2}$$のような、文字式÷数 の形の割り算を学習します。
中学2年生では、$${6x÷2x}$$のような、文字式÷文字式 の形の割り算を学習します。
教科書の解き方を見ると、どちらもこのように解いています。

でも、中学2年生の授業で、図1の右の計算を示すと、首をひねっている生徒がいたので聞いてみると、こんな疑問をもっていました。

2 割り算の2通りの解釈
割り算には、2通りの解釈があります。
6÷2を例にして、説明します。
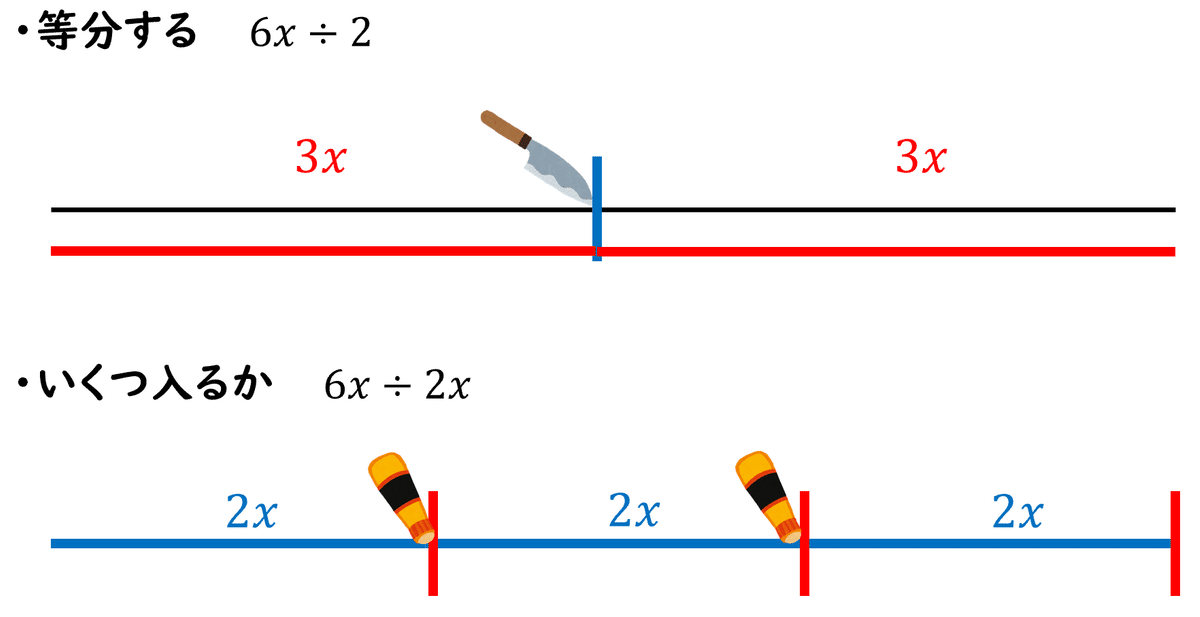
・等分する
6を2等分すると、いくつずつに分けられるか(これが商になる)という式の解釈です。
・いくつ入るか
6の中に2がいくつ入るか(これが商になる)という式の解釈です。
この記事では、割り算はこの解釈で進めていきます。
・なぜ2通りの解釈ができるのか
その理由は、乗法の交換法則が成り立つからです。
要は、掛け算の場合、かける順序を入れ替えても、答えは変わらないという法則です。
この法則があるため、割り算は2通りの解釈ができます。

3 中学1年生と2年生の文字式の割り算は解釈を変える
図2の生徒の疑問を解決するには、中学1年生と2年生の割り算は解釈を変えないといけないことを伝えないといけません。
中学1年生では「等分する」解釈、中学2年生では「いくつ入るか」解釈になります。
こう伝えると、生徒も納得してくれるでしょう。
これで$${6x÷2x=3}$$という計算結果は、もっともらしいといえます。
この捉え方をした後に、図1を示した方がいいと思います。
4 最後に
生徒にこの説明をしながら考えたのは、$${6ab÷2a}$$はどう捉えるか、です。
この割り算は$${6ab}$$という面積の長方形の一辺が$${2a}$$と分かっているとき、もう一辺の長さは何か?という捉え方になると思います。

この捉え方は、生徒たちは前時で文字式同士の掛け算で学習しているので、すんなり入ると思います。
ちなみに、図5の捉え方は、割り算の「いくつ入るか」という捉え方と同じです。
今回の記事では、数学の教師にとっては当たり前(図1のような計算)でも、生徒にとっては捉え方が何の前触れもなく変わってしまって難しい、というものを紹介しました。
生徒の何気ない疑問は、教師として大事にしていきたいですね。
最後まで読んでいただき、ありがとうございました!!

この記事が気に入ったらサポートをしてみませんか?
