数学美術館（プラトンの立体）

　こんにちは。
　今回は、プラトンの立体について紹介します。

　この美術館のコンセプトは、数学の厳密さではなく「見て楽しむ」重視ですので、数学嫌いな方でも「なるほど～」「面白い」と感じていただけるような記事にしますので、ぜひ読んでいただけるとうれしいです。

・　プラトンの立体とは？

　プラトンの立体とは、下の写真の５つです。
　面の形は、
　正三角形・・・正四面体、正八面体、正二十面体
　正方形　・・・正六面体
　正五角形・・・正十二面体

プラトンの立体（百均で購入）

　プラトンの立体は、正多面体ともいい、この世に正多面体はこの５つしかないことが証明されています。

・　正六面体と正八面体は親子！？

　正六面体の各面の重心を見つけて、その点をつなぎます。
　そうすると、正八面体ができます。

　同様に、正八面体の各面の重心をつなげると、正十二面体ができます。

美術品№１　正六面体と正八面体は親子！？

　ちなみに、正六面体と正八面体は頂点の数と面の数が入れ替わった図形になっています。

・　正十二面体と正二十面体は親子！？

　正六面体と正八面体と同じような操作を正十二面体と正二十面体にしてみます。

美術品№２　正十二面体から正二十面体が作れる

美術品№３　正二十面体から正十二面体が作れる

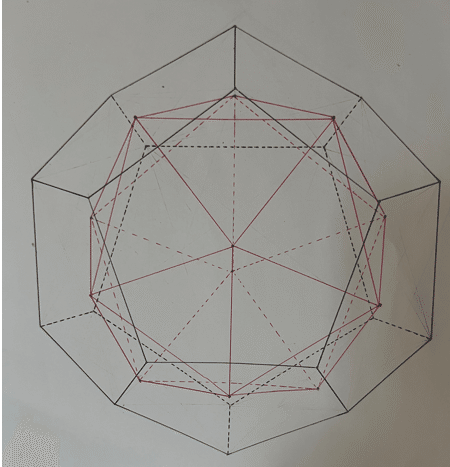
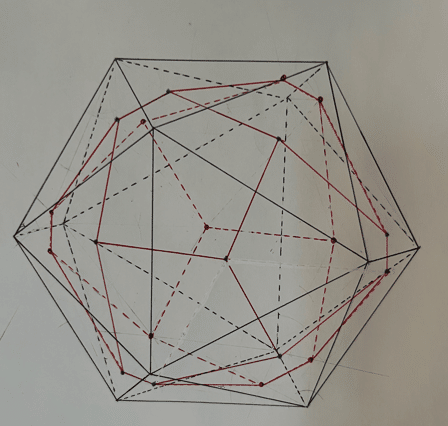
　ちなみに、正十二面体と正二十面体は頂点の数と面の数が入れ替わった図形になっています。

・　正四面体は自己増殖！？

　正六面体と正八面体、正十二面体と正二十面体がペア。
　では、残った正四面体のペアは？

　実は、正四面体は自分自身がペアです。

美術品№４　正四面体は自己増殖！？

・　黄金長方形で作れるプラトンの立体

　横の長さを１、縦の長さをΦの長方形を３枚用意します。
　Φは黄金比です。
　$${Φ=\frac{1+\sqrt{5}}{2}}$$

黄金長方形３枚

　この黄金長方形を3枚、次のようにそれぞれが直角に交わるように組み立てます。ちなみに上の写真の切込みは、組み立てるためです。

黄金長方形を３枚直角に組み立てる

　この黄金長方形の１２個の頂点を結ぶと、正二十面体ができます。

美術品№５　黄金長方形で作った正二十面体

　少し見づらくてすみません。

　次に黄金長方形の１２枚の頂点が正五角形の重心にくれば、正十二面体が作れます。

美術品№６　黄金長方形で作った正十二面体

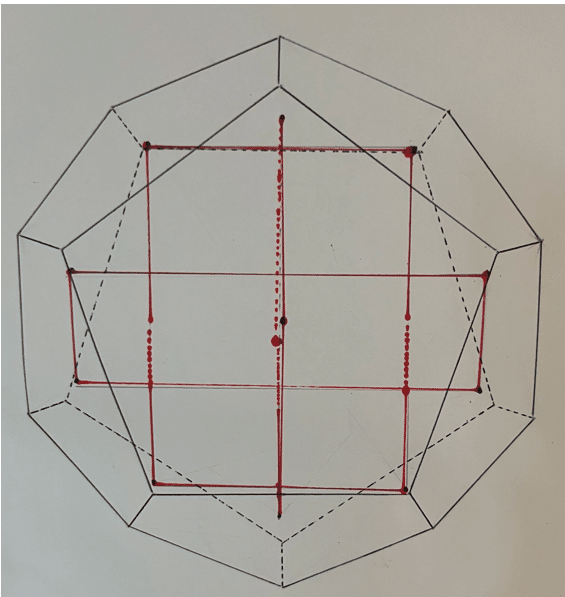
おわりに

　今回はプラトンの立体に関する性質を紹介しました。

　まだまだ他にもこの記事で紹介できなかった面白い性質があります。

　知れば知るほど面白いですし、なぜプラトンがこの５つの立体を見いだせたのか調べていくと、数学史をより知りたいという気持ちにさせられます。

　私も新たな知見を得られれば、加筆していきたいと思います。

　最後まで読んでいただき、ありがとうございました！！