
ピーターのコイントスから見る繰り返し投資行動の数理
世の中の投資行動には基本的に全て、得をする可能性もあれば損をする可能性もあります。
絶対に得をする投資行動は投資家が群がり儲からなくなってしまいますし、絶対に損をする投資行動は誰も行いません。
投資行動を行った際の最終的な期待値がプラスになる投資行動を繰り返せば確実に儲けることができます。
しかしこの「期待値」として、投資行動を一回行った際の単純な期待値を考えてしまうと、実は一見すると期待値は正なのに最終的にほぼ確実に損をしてしまうことがあります。
ピータースのコイントス
次の投資行動を考えてみましょう(ピータースのコイントス)。
コインを投げて表がでたら所持金の50%が追加で貰える
裏がでたら所持金の40%を失う
この投資行動の単純な期待値を計算すると
$$
\displaystyle \frac{1}{2} \times 0.5 - \frac{1}{2} \times 0.4 = 0.05
$$
となりますから、一見すると所持金が5%ずつ増えていくと考えられそうです。
そう思った方は次のシミュレータを試してみてください。
実際にシミュレーションを行うと、試行回数が多ければ多いほど、みるみるうちに所持金は減っていってしまいます。
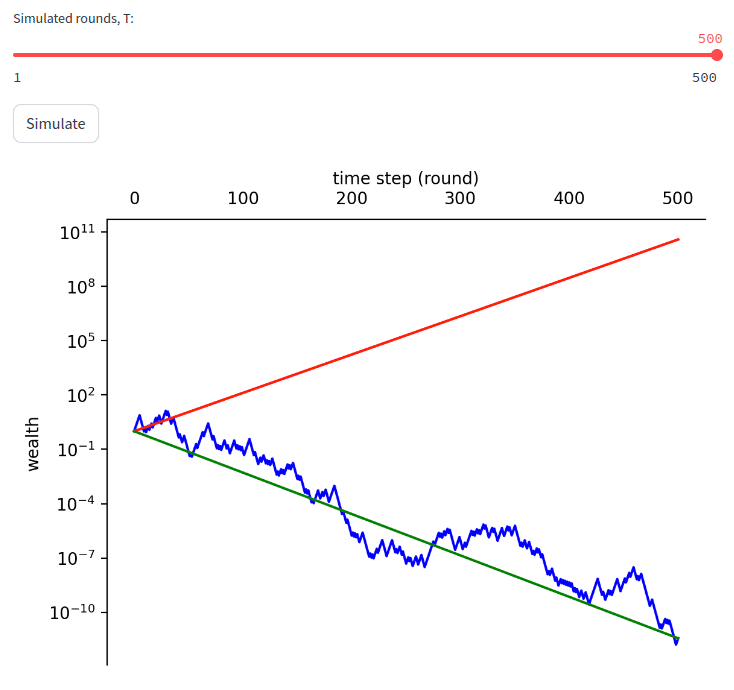
「それはたまたま運が悪かっただけだ」と思う方はシミュレートボタンを何回も押してみてください。
何回押したとしても最終的に増えることはほぼ起きません。
パラドクスの直感的理解
まずは数学的な考察はおいておいて、この現象を直感的に理解します。
コインの裏が一度でもでてしまうと、次に賭けることのできる金額が大幅に減ってしまうため、もし負けたあとに勝ったとしても得られることのできる賞金は大きく目減りしてしまいます。
もちろん勝ち続ければいいのですが、一度でも負けてしまうとそれを挽回するのは簡単ではありません。
例えば一度負けてから勝ったとすると、$${0.6 \times 1.5 = 0.9}$$となり最終的な損益としてはマイナス10%です。
勝ってから負けたとしても$${1.5 \times 0.6 = 0.9}$$ですので同じくマイナス10%となります。
そのため何回もこの投資行動を繰り返すと資産はどんどんと目減りしていってしまうのです。
算術平均と幾何平均
それでは数学的な解析を始めましょう。
この投資行動を一度行った場合にはすでに計算したとおりプラス5%の損益となります。
しかし、これをN回行った場合にはどうなるでしょうか?
Nが十分大きければ勝つ回数と負ける回数は同じ回数になるはずですので、最終的な損益の期待値は
$$
1.5^{N/2} \times 0.6^{N/2} = 0.9^{N/2}
$$
となります。
つまり、一回ごとに指数関数的に負け越してしまいます。
一回あたりの資産の増減率はこれを 1/N 乗して
$$
0.9^{1/2} \simeq 0.9487
$$
と概ね5%ずつ減っていくことになります。
そのため、投資行動が一度きりだった場合には単純な平均(算術平均、といいます)で期待値を計算できますが、投資行動を無限に繰り返すことができる場合にはこのように幾何平均、すなわち
$$
1.5^{1/2} \times 0.9^{1/2}
$$
を採用する必要があります。
この式の対数をとると
$$
\displaystyle \frac{1}{2} \ln 1.5 + \frac{1}{2} \ln 0.9
$$
という式になりますので、確率変数 X の期待値を $${\braket{X}}$$ と表すことにすると、試行回数が一回の場合には
$$
\braket{X}
$$
を計算すればいいのですが、無限に繰り返せる場合には
$$
\exp \braket{\ln X}
$$
を計算しなければいけないということを意味します。
この式のことを「幾何的期待成長率 (expected geometric growth rate)」といいます。
繰り返し投資行動の場合にはこの幾何的期待成長率を計算する必要があるのです。
ケリー基準
幾何的期待成長率は、投資行動を行う際に全財産をベットするのではなく、ある一定割合だけをベットすることで最適化することができます。
この最適な投資割合のことを「ケリー基準 (Kelly criterion)」といいます。
証明はリンク先のWikipediaの記事に譲ることにして計算結果のみを記載すると、投資成功確率を p、失敗時の損失率を a、成功時の利益率を b とすると
$$
\displaystyle f^* = \frac{p}{a} - \frac{1-p}{b}
$$
が最適なベット額となります。
ピータースのコイントスの場合には a = 0.4、b = 0.5、p = 0.5 ですので
$$
\frac{0.5}{0.4} - \frac{0.5}{0.5} = 0.25
$$
となり、全財産の25%をベットすればいいとわかります。
全財産の100% (f = 1) をベットすると資産を失ってしまいますが、ケリー基準に従って投資を行えば資産はみるみるうちに増えていきます(演習問題①)。
エルゴード性
ピータースのコイントスは、古典力学などで有名な「エルゴード性」と呼ばれる性質を失う例として考案されました。
エルゴード性とは「集団(アンサンブル)平均と長時間平均が一致すること」を表しています。
……といっても何のことか分からないと思うので説明すると、ピータースのコイントスの場合には、もし参加者が無限にいてその参加者が一斉にコイントスをすれば算術平均どおりに全参加者の資産合計額は増えます(集団平均)。
しかし、一個人の資産にだけ着目すると長い目で見る(長時間平均)と確実に損をしてしまいます。
視点を「集団として」みるのか「一個人だけ」をみるのかによって平均値が変わらないという性質をエルゴード性といい、一般的な力学系などでは必ずこの性質を満たす(統計力学における等重率の原理の根拠であると一般的に言われているが、その話をすると本が一冊出来上がるので割愛します)のですが、今回のような特殊なケースでは成り立たないということになります。
まぁ難しい話は全部忘れてもらうと「全体が儲かっている/損しているからといって、個々人がそうとは限らない」という感じですかね(適当)。
そういう高尚な話が背景にあるんだよ、ということだけ分かってもらえればOKです。
演習問題
①:ケリー基準に従った際のピータースのコイントスの幾何的期待成長率
これを計算せよ。(答え:$${{\sqrt{81/80} = 1.00623}}$$)
②:ベット割合を f としたときの幾何的期待成長率を f の関数として表せ。また f = 0.25 で最大となることを確認せよ
答え:

この記事が気に入ったらサポートをしてみませんか?
