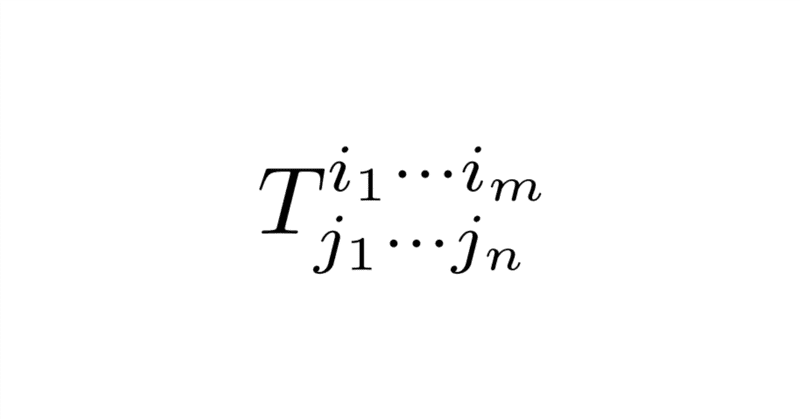
テンソルが意味不明な物理学習者へ: 共変ベクトルと反変ベクトルからテンソルまで

　物理の本ではよく, 「反変ベクトルとは～～という変換則をもち, 共変ベクトルは・・・という変換則をもつものとして定義される」と説明がなされますが, 初学者にとってはなぜ唐突にこのような定義がされるのか非常にわかりにくいと思います.

　そこでこのページでは数学的によりシンプルな定義を採用し, 一点の曇りなく自然に反変ベクトルと共変ベクトルが導入されることを説明します. さらに2つの拡張としてテンソルが自然に導入されることもみていきます.

　以下では$${\left(e_i\right)_{1\leq i\leq n}}$$を$${n}$$次元実ベクトル空間$${V}$$の基底とします. 複素ベクトル空間の場合も以下の$${\mathbb{R}}$$を$${\mathbb{C}}$$に変えるだけで全て上手く成り立ちます.

　このページと同じ内容のPDFも用意していますので適宜ご利用ください.

tensor.pdf

159 KB

ファイルダウンロードについて

ダウンロード

前提知識: Einsteinの縮約則

　以下、上下で同じ添え字がある場合は和をとるEinsteinの縮約則を採用します. 例えば, 本来

$$
x^1y_1+\cdots+x^ny_n=\sum^n_{i=1}x^iy_i
$$

とかくのを略記して

$$
x^1y_1+\cdots+x^ny_n=x^iy_i
$$

とします. 他にも

$$
\left(a^1,\cdots,a^n\right)\left(
\begin{matrix}
A_{11} & \cdots & A_{1n} \\
\vdots & \ddots & \vdots \\
A_{n1} & \cdots & A_{nn}
\end{matrix}
\right)\left(
\begin{matrix}
b^1 \\
\vdots \\
b^n
\end{matrix}
\right)=\sum^n_{i=1}\sum^n_{j=1}a^iA_{ij}b^j
$$

ですが,

$$
\left(a^1,\cdots,a^n\right)\left(
\begin{matrix}
A_{11} & \cdots & A_{1n} \\
\vdots & \ddots & \vdots \\
A_{n1} & \cdots & A_{nn}
\end{matrix}
\right)\left(
\begin{matrix}
b^1 \\
\vdots \\
b^n
\end{matrix}
\right)=a^iA_{ij}b^j
$$

と略記します.

反変ベクトルと共変ベクトルの定義

定義1: 反変ベクトル
反変ベクトル（contravariant vector）とは$${V}$$の元のことである

　例えば$${{V}=\mathbb{R}^n}$$なら$${\bm{x}=\left(x_1,x_2,\cdots,x_n\right)^T\in\mathbb{R}^n}$$は全て反変ベクトルです. つまり反変ベクトルとは単純にベクトル空間の元のことなのです. これと物理流の定義がどう繋がるかは順を追って説明します.

　その前に共変ベクトルも定義しておきましょう. 準備として以下の概念を導入します（普通の線形代数の教科書に載っていることが多いです）.

定義2: 双対ベクトル空間
　$${V^{*}\coloneqq\{T:V\rightarrow\mathbb{R}|T:\text{線形写像}\}}$$
を$${V}$$の双対ベクトル空間(dual vector space）という
ただし加法とスカラー倍は
　$${\left(T+U\right)\left(v\right)\coloneqq T\left(v\right)+U\left(v\right)\qquad\left(v\in V\right)}$$
　$${\left(aT\right)\left(v\right)\coloneqq a\cdot T\left(v\right)\qquad\left(a\in\mathbb{R},v\in V\right)}$$
で定義される

　$${V^{*}}$$が実際にベクトル空間であることは容易にわかりますが, 実は$${V^{*}}$$が$${V}$$と同じ$${n}$$次元であることが以下のようにして確かめられます.

　まず、線形写像$${T:V\rightarrow\mathbb{R}}$$は$${V}$$の基底$${\left(e_i\right)_{1\leq i\leq n}}$$での値のみで定まることに注意します. 実際任意の$${v=v^1e_1+\cdots+v^ne_n\in V\left(v^1,\cdots,v^n\in\mathbb{R}\right)}$$に対して, $${T}$$の線形性から

$$
T\left(v\right)=v^1T\left(e_1\right)+\cdots+v^nT\left(e_n\right)
$$

のように$${T\left(v\right)}$$の値が決まってしまいます。一般の集合の間の写像は, 引数1つ1つに対応する値を定めなければ定まりませんが, 線形写像に限ってはこのような特別なことが起きます.
（一般に環$${R}$$上の自由加群から任意の$${R}$$加群への$${R}$$準同型写像は基底での値のみで決まる）

次に線形写像の族$${\left(f^i\right)_{1\leq i\leq n}}$$を

$$
f^i\left(e_j\right)\coloneqq\delta^i_j
$$

で定めます. ただし$${\delta^i_j}$$はKroneckerデルタ

$$
\delta^i_j=\Bigg\{\begin{aligned}1\ \left(i=j\right)\\0\ \left(i\neq j\right)\end{aligned}
$$

です. $${V}$$の基底$${\left(e_i\right)_{1\leq i\leq n}}$$の添え字を下にしたので, のちにEinsteinの縮約則を使えるように$${\left(f^i\right)_{1\leq i\leq n}}$$の添え字は上にしました.

　任意の線形写像$${T:V\rightarrow\mathbb{R}}$$に対し,

$$
T\left(e_1\right)=a_1,\cdots,T\left(e_n\right)=a_n\in\mathbb{R}
$$

なら, $${T=a_1f^1+\cdots+a_nf^n}$$と表せます. これは両辺に$${e_1,\cdots,e_n}$$を順次代入することでわかります. 先ほど説明した通り, 線形写像は基底での値のみで定まってしまうことに留意しましょう.

　以上で$${\left(f^i\right)_{1\leq i\leq n}}$$がベクトル空間$${V^*}$$を張っていることがわかりました. さらに$${\left(f^i\right)_{1\leq i\leq n}}$$は一次独立です. なぜなら

$$
c_1f^1+\cdots+c_nf^n=0\qquad\left(c_1,\cdots,c_n\in\mathbb{R}\right)
$$

とすると, $${e_1,\cdots,e_n}$$を順次代入することで$${c_1=\cdots=c_n=0}$$がわかるからです. こうして$${V^*}$$が$${n}$$次元ベクトル空間で, $${\left(f^i\right)_{1\leq i\leq n}}$$がその基底になっていることがわかりました. $${\left(f^i\right)_{1\leq i\leq n}}$$は$${\left(e_i\right)_{1\leq i\leq n}}$$の双対基底（dual basis）とよばれます.

定義3: 共変ベクトル
共変ベクトル（covariant vector）とは$${V^*}$$の元のことである

　よく物理の本では「反変ベクトルと共変ベクトルは足し引きすることができない」と急に言われれますが, それは両者の住んでいる空間が異なるので至極当然のことなのです.

なぜ"反変", "共変"か？

　基底$${\left(e_i\right)_{1\leq i\leq n}}$$が正則行列$${A=\left(A^j_i\right)_{1\leq i,j\leq n}}$$によって基底変換

$$
e_i\rightarrow\bar{e}_i=A^j_ie_j \\
\left(\text{行列表示: }\left(\bar{e}_1,\cdots,\bar{e}_n\right)=\left(e_1,\cdots,e_n\right)A\right)
$$

を受ける状況を考えましょう（基底変換は物理的には座標軸を取り直す座標変換に対応します）. Einsteinの縮約則を採用していることに注意してください. 今回は$${j}$$について和をとっています.

　変換後の$${\left(\bar{e_i}\right)_{1\leq i\leq n}}$$が実際に$${V}$$の基底であることは簡単な線形代数の問題ですので, ぜひ自力で示してみましょう.

　さて, このとき任意の$${v\in V}$$は

$$
\begin{array}{}
v & = & v^1e_1+\cdots+v^ne_n\qquad\left(v^1,\cdots,v^n\in\mathbb{R}\right) \\
& = & \bar{v}^{1}\bar{e}_1+\cdots+\bar{v}^{n}\bar{e}_n\qquad\left(\bar{v}^1,\cdots,\bar{v}^n\in\mathbb{R}\right)
\end{array}
$$

のように2通りに表示できます. $${V}$$の基底$${\left(e_i\right)_{1\leq i\leq n}}$$の添え字を下にしたので, Einsteinの縮約則がわかりやすいように成分$${v^1,\cdots,v^n,\bar{v}^1,\cdots,\bar{v}^n\in\mathbb{R}}$$の添え字は上にかきました. 以降反変ベクトルの成分の添え字は上付きにします.

　ここで2通りの成分$${v_i}$$と$${\bar{v}_i}$$の関係を求めてみましょう.

$$
\begin{aligned}
v^ie_i & =\bar{v}^i\bar{e}_i \\
& =\bar{v}^iA^j_ie_j \\
& =\left(A^i_j\bar{v}^j\right)e_i
\end{aligned}
$$

ただし, 最後の等号ではダミーの添え字である$${i}$$と$${j}$$を入れ替えています（以下, ダミー添え字の入れ替えを頻繁に行います）. $${e_1,\cdots,e_n}$$は一次独立なので, 成分同士を比較して

$$
\begin{aligned}
v^i=A^i_j\bar{v}^j & \iff \left(\begin{matrix}v^1\\ \vdots\\ v^n\end{matrix}\right)=A\left(\begin{matrix}\bar{v}^1\\ \vdots\\ \bar{v}^n\end{matrix}\right) \\
& \iff\left(\begin{matrix}\bar{v}^1\\ \vdots\\ \bar{v}^n\end{matrix}\right)=A^{-1}\left(\begin{matrix}v^1\\ \vdots\\ v^n\end{matrix}\right) \\
& \iff\bar{v}^i=\left(A^{-1}\right)^i_jv^j
\end{aligned}
$$

という変換規則が得られます. 成分$${v^i}$$が基底変換の逆行列$${A^{-1}}$$で変換を受けている（反対の変換を受けている）から"反変"ベクトルなのです. 今回の定義は物理流の「$${v^i\rightarrow\bar{v}^i=\left(A^{-1}\right)^i_jv^j}$$という変換性をもつ対象」という反変ベクトルの定義を再現しています. しかも今回の定義の方が唐突でなく, 俄然受け入れやすいと思います.

　ここまでくれば"共変"の由来も見えてきたのではないでしょうか. まず, $${\left(e_i\right)_{1\leq i\leq n}}$$が$${\left(\bar{e}_i=A^j_ie_j\right)_{1\leq i\leq n}}$$に基底変換されたとき, 双対基底$${\left(f^i\right)_{1\leq i\leq n}}$$がどのように変換されるか見てみましょう.

　$${\left(\bar{e}_i\right)_{1\leq i\leq n}}$$の双対基底$${\left(\bar{f}^i\right)_{1\leq i\leq n}}$$は

$$
\bar{f}^i\left(\bar{e}_j\right)\coloneqq\delta^i_j
$$

で定義されるので

$$
\begin{aligned}
\delta^i_j & =\bar{f}^i\left(\bar{e}_j\right)=\bar{f}^i\left(A^k_je_k\right)=A^k_j\bar{f}^i\left(e_k\right)\qquad\left(\because\bar{f}^i\text{は線形写像}\right) \\
& \implies \left(A^{-1}\right)^i_l= \delta^k_l\bar{f}^i\left(e_k\right)=\bar{f}^i\left(e_l\right)\qquad\left(\because\text{両辺に}\times\left(A^{-1}\right)^j_l\right) \\
& \implies \delta^m_l=A^m_i\bar{f}^i\left(e_l\right)\qquad\left(\because\text{両辺に}\times A^m_i\right) \\
& \implies f^m\left(e_l\right)=A^m_i\bar{f}^i\left(e_l\right) \\
\\
\therefore & A^m_i\bar{f}^i=f^m
\end{aligned}
$$

が成り立ちます（添え字が多いけど頑張って！！）. 線形写像が基底での値のみで決まることから, 最終行のように$${A^m_i\bar{f}^i}$$と$${f^m}$$が写像として一致していることがわかります.

　これより

$$
\begin{aligned}
f^i=A^i_j\bar{f}^j & \iff\left(\begin{matrix}f^1\\ \vdots\\ f^n\end{matrix}\right)=A\left(\begin{matrix}\bar{f}^1\\ \vdots\\ \bar{f}^n\end{matrix}\right) \\
& \iff\left(\begin{matrix}\bar{f}^1\\ \vdots\\ \bar{f}^n\end{matrix}\right)=A^{-1}\left(\begin{matrix}f^1\\ \vdots\\ f^n\end{matrix}\right) \\
& \iff\bar{f}^i=\left(A^{-1}\right)^i_jf^j
\end{aligned}
$$

　基底$${\left(e_i\right)_{1\leq i\leq n}}$$の変換に対する双対基底$${\left(f^i\right)_{1\leq i\leq n}}$$の変換性が分かったので, 今度は成分の変換性をみていきます. 任意の$${T\in V^*}$$は

$$
\begin{aligned}
T & =a_1f^1+\cdots+a_nf^n\qquad\left(a_1,\cdots,a_n\in\mathbb{R}\right) \\
& =\bar{a}_{1}\bar{f}^1+\cdots+\bar{a}_{n}\bar{f}^n\qquad\left(\bar{a}_1,\cdots,\bar{a}_n\in\mathbb{R}\right)
\end{aligned}
$$

と2通りに表示できます. $${V^*}$$の基底$${\left(f^i\right)_{1\leq i\leq n}}$$の添え字は上だったので, Einsteinの縮約則に則るように成分$${a_1,\cdots,a_n,\bar{a}_1,\cdots,\bar{a}_n\in\mathbb{R}}$$の添え字は下に付けました.

　このとき

$$
\begin{aligned}
a_if^i & =\bar{a}_i\bar{f}^i \\
& =\bar{a}_i\left(A^{-1}\right)^i_jf^j \\
& =\bar{a}_j\left(A^{-1}\right)^j_if^i
\end{aligned}
$$

$${f^1,\cdots,f^n}$$は一次独立なので, 成分ごとに比較できて

$$
\begin{aligned}
a_i=\bar{a}_j\left(A^{-1}\right)^j_i & \iff\left(a_1,\cdots,a_n\right)=\left(\bar{a}_1,\cdots,\bar{a}_n\right)A^{-1} \\
& \iff\left(\bar{a}_1,\cdots,\bar{a}_n\right)=\left(a_1,\cdots,a_n\right)A \\
& \iff\bar{a}_i=a_jA^j_i
\end{aligned}
$$

という変換規則が得られます. 成分$${a_i}$$が$${V}$$の基底変換と一緒の行列$${A}$$で変換を受けている（共通の変換を受けている）から"共変"ベクトルなのです. 共変ベクトルでも物理流の変換性による定義が再現されていることが確認できました.

　以上をまとめると,

反変ベクトルの基底$${\left(e_i\right)_{1\leq i\leq n}}$$が
　$${e_i\rightarrow\bar{e}_i=A^j_ie_j}$$
と基底変換されたとき,
　・反変ベクトルの成分: 添え字は上, $${v^i\rightarrow\bar{v}^i=\left(A^{-1}\right)^i_jv^j}$$
　・共変ベクトルの基底: 添え字は上, $${f^i\rightarrow\bar{f}^i=\left(A^{-1}\right)^i_jf^j}$$
　・共変ベクトルの成分: 添え字は下, $${a_i\rightarrow\bar{a}_i=A^j_ia_j}$$

　つまり, 物理流の反変ベクトルと共変ベクトルの定義はベクトル空間$${V}$$の基底を変換したときに, $${V}$$と双対空間$${V^*}$$の元の成分$${\in\mathbb{R}}$$がどのように変換するかを定めたものなのです.

　添え字は反変ベクトルの成分が上で共変ベクトルの成分が下になっていますが, これはどの物理の本を読んでも同じになっている統一的な習慣です.

テンソル

　いよいよテンソルの話に行きたいのですが, まずテンソルの集合であるテンソル積空間を定義したいと思います。物理でいう"テンソル"とは, このテンソル積空間の特別な場合の元のことです.

定義4: ベクトル空間のテンソル積空間
　ベクトル空間$${V_1}$$,$${V_2}$$のテンソル積（tensor product）とは, ベクトル空間$${V_1\otimes V_2}$$と写像$${\phi:V_1\times V_2\rightarrow V_1\otimes V_2}$$の組$${\left(V_1\otimes V_2,\phi\right)}$$であって, 以下の普遍性（universality）（＊）を満たすものである:
　（＊）任意のベクトル空間$${W}$$と双線形写像$${f:V_1\times V_2\rightarrow W}$$に対し, $${f=g\circ\phi}$$を満たす$${g:V_1\otimes V_2\rightarrow W}$$が一意に存在する.

　定義4はテンソル積空間の数学的に最も一般的な定義ですが, 正直なところ, 特に物理畑の人にとっては, さっぱり意味が伝わらないと思います. そこでもう少しかみ砕いた表現に言い換えてみましょう.

定義4’: テンソル積空間
　ベクトル空間$${V_1}$$,$${V_2}$$（$${\dim V_1=k,\dim V_2=l}$$）の基底をそれぞれ$${\left(e^1_i\right)_{1\leq i\leq k}}$$, $${\left(e^2_i\right)_{1\leq i\leq l}}$$とするとき, $${V_1}$$と$${V_2}$$のテンソル積（tensor product）$${V_1\otimes V_2}$$とは, $${\left(e^1_i\otimes e^2_j\right)_{1\leq i\leq k,1\leq j\leq l}}$$を基底とする$${kl}$$次元ベクトル空間のことである.
　ただし, $${c\in\mathbb{R}}$$, $${v_1\in V_1}$$, $${v_2\in V_2}$$に対し,
　$${c\left(v_1\otimes v_2\right)=\left(cv_1\right)\otimes v_2=v_1\otimes\left(cv_2\right)}$$
という関係があるものとする.

　この定義は若干数学的厳密性を欠いていますが, 直感的にわかりやすいので物理でテンソルを扱うには十分だと思われます. 定義4から定義4'が導かれることの詳細を知りたければ, 上級の線形代数の教科書か可換環論の本を参照してください.

　テンソル積は3つ以上のベクトル空間に対しても定義ができて,

$$
V_1\otimes V_2\otimes\cdots\otimes V_n
$$

と表記され,

$$
\begin{aligned}
c\left(v_1\otimes v_2\otimes\cdots\otimes v_n\right) & =\left(cv_1\right)\otimes v_2\otimes\cdots\otimes v_n \\
& =v_1\otimes\left(cv_2\right)\otimes\cdots\otimes v_n \\
& =\cdots \\
& =v_1\otimes v_2\otimes\cdots\otimes\left(cv_n\right)
\end{aligned}
$$

です. また基底は

$$
\left(e^1_{i_1}\otimes e^2_{i_2}\otimes\cdots\otimes e^n_{i_n}\right)_{1\leq i_1\leq\dim V_1,1\leq i_2\leq\dim V_2,\cdots,1\leq i_n\leq\dim V_n}
$$

で与えられ, $${V_1\otimes V_2\otimes\cdots\otimes V_n}$$は$${\dim V_1\times\dim V_2\times\cdots\times\dim V_n}$$次元です.

　さて, いよいよ物理で使われるテンソルの定義にまいりましょう.

定義5: （物理の）テンソル
　物理でいう$${\left(k,l\right)}$$テンソルまたは$${k}$$階反変$${l}$$階共変テンソルとは, $${\underbrace{V\otimes\cdots\otimes V}_{k}\otimes\underbrace{V^*\otimes\cdots\otimes V^*}_{l}}$$（以降$${\left(\bigotimes^kV\right)\otimes\left(\bigotimes^lV^*\right)}$$と略記する）の元のことである.

　実は反変ベクトルは$${\left(1,0\right)}$$テンソル, 共変ベクトルは$${\left(0,1\right)}$$テンソルです.

　物理の本でよく出てくるテンソルの表記$${T^{i_1\cdots i_k}_{j_1\cdots j_l}}$$とこの定義は一向に姿が違うじゃないか！と思う方もいらっしゃるかもしれませんが, 安心してください. 今から今回の定義との繋がりをみていきます.

　$${\left(\bigotimes^kV\right)\otimes\left(\bigotimes^lV^*\right)}$$の基底は

$$
\Big(\underbrace{e_{i_1}\otimes\cdots\otimes e_{i_k}}_{k}\otimes\underbrace{f^{j_1}\otimes\cdots\otimes f^{j_l}}_{l}\Big)_{1\leq i_1,\cdots,i_k,j_1,\cdots,j_l\leq n}
$$

で与えられます（$${\dim V=n}$$なら$${\dim V^*=n}$$だったことに注意！）. 例えば$${\dim V=2}$$の場合, $${\left(1,1\right)}$$テンソル（1階反変1階共変テンソル）のなす空間$${V\otimes V^*}$$の基底は

$$
\left(e_1\otimes f^1,e_1\otimes f^2,e_2\otimes f^1, e_2\otimes f^2\right)
$$

の4つです. このことを用いると, 任意の$${\left(l,k\right)}$$テンソル$${T\in\left(\bigotimes^kV\right)\otimes\left(\bigotimes^lV^*\right)}$$は

$$
T=\sum^n_{i_1=1}\cdots\sum^n_{i_k=1}\sum^n_{j_1=1}\cdots\sum^n_{j_l=1} T^{i_1\cdots i_k}_{j_1\cdots j_l}e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}\\
\left(T^{i_1\cdots i_k}_{j_1\cdots j_l}\in\mathbb{R}\right)
$$

と展開されます. ただし, わかりやすさのためにシグマ記号を明示しておきました. 通常, 物理の本では各基底$${e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}}$$に対応する成分$${T^{i_1\cdots i_k}_{j_1\cdots j_l}\in\mathbb{R}}$$がテンソルとよばれています.

　さて, 物理の本ではテンソルも変換性で定義されている場合が多いと思いますが, 共変ベクトル・反変ベクトルと同様に, 今回の定義からその変換性が導かれることを確認しましょう.

　例によって$${V}$$の基底$${\left(e_i\right)_{1\leq i\leq n}}$$が基底変換

$$
e_i\rightarrow\bar{e}_i=A^j_ie_j \\
$$

を受ける場合を考えましょう. 同時に双対基底$${\left(f^i\right)_{1\leq i\leq n}\subset V^*}$$は

$$
f^i\rightarrow\bar{f}^i=\left(A^{-1}\right)^i_jf^j \\
$$

と変換されたことを思い出してください. このとき, テンソル積空間$${\left(\bigotimes^kV\right)\otimes\left(\bigotimes^lV^*\right)}$$の基底$${\left(e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}\right)_{1\leq i_1,\cdots,i_k,j_1,\cdots,j_l\leq n}}$$は次のように変換を受けます.

$$
\begin{aligned}
& e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l} \\
\rightarrow & \quad\bar{e}_{i_1}\otimes\cdots\otimes \bar{e}_{i_k}\otimes \bar{f}^{j_1}\otimes\cdots\otimes \bar{f}^{j_l} & =\left(A^{a_1}_{i_1}e_{a_1}\right)\otimes\cdots\otimes \left(A^{a_k}_{i_1}e_{a_k}\right)\otimes\left(\left(A^{-1}\right)^{j_1}_{b_1}f^{b_1}\right)\otimes\cdots\otimes\left(\left(A^{-1}\right)^{j_l}_{b_l}f^{b_l}\right) \\
& & =A^{a_1}_{i_1}\cdots A^{a_k}_{i_1}\left(A^{-1}\right)^{j_1}_{b_1}\cdots\left(A^{-1}\right)^{j_l}_{b_l}\left(e_{a_1}\otimes\cdots\otimes e_{a_k}\otimes f^{b_1}\otimes\cdots\otimes f^{b_l}\right)
\end{aligned}
$$

　次に, おなじみの操作になってきましたが$${T\in\left(\bigotimes^kV\right)\otimes\left(\bigotimes^lV^*\right)}$$を2種類の基底$${\left(e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}\right)_{1\leq i_1,\cdots,i_k,j_1,\cdots,j_l\leq n}}$$, $${\left(\bar{e}_{i_1}\otimes\cdots\otimes \bar{e}_{i_k}\otimes \bar{f}^{j_1}\otimes\cdots\otimes \bar{f}^{j_l}\right)_{1\leq i_1,\cdots,i_k,j_1,\cdots,j_l\leq n}}$$を用いて展開してみます.

$$
\begin{aligned}
T & = & T^{i_1\cdots i_k}_{j_1\cdots j_l}e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}\qquad\left(T^{i_1\cdots i_k}_{j_1\cdots j_l}\in\mathbb{R}\right) \\
& = & \overline{T}^{i_1\cdots i_k}_{j_1\cdots j_l}\bar{e}_{i_1}\otimes\cdots\otimes \bar{e}_{i_k}\otimes \bar{f}^{j_1}\otimes\cdots\otimes \bar{f}^{j_l}\qquad\left(\overline{T}^{i_1\cdots i_k}_{j_1\cdots j_l}\in\mathbb{R}\right)
\end{aligned}
$$

ただしEinsteinの縮約則を再び採用しシグマ記号を省略しました.

　このとき

$$
\begin{aligned}
T^{i_1\cdots i_k}_{j_1\cdots j_l}e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l} & =\overline{T}^{i_1\cdots i_k}_{j_1\cdots j_l}\bar{e}_{i_1}\otimes\cdots\otimes \bar{e}_{i_k}\otimes \bar{f}^{j_1}\otimes\cdots\otimes \bar{f}^{j_l} \\
& =\overline{T}^{i_1\cdots i_k}_{j_1\cdots j_l}A^{a_1}_{i_1}\cdots A^{a_k}_{i_1}\left(A^{-1}\right)^{j_1}_{b_1}\cdots\left(A^{-1}\right)^{j_l}_{b_l}\left(e_{a_1}\otimes\cdots\otimes e_{a_k}\otimes f^{b_1}\otimes\cdots\otimes f^{b_l}\right) \\
& =\overline{T}^{a_1\cdots a_k}_{b_1\cdots b_l}A^{i_1}_{a_1}\cdots A^{i_k}_{a_1}\left(A^{-1}\right)^{b_1}_{j_1}\cdots\left(A^{-1}\right)^{b_l}_{j_l}\left(e_{i_1}\otimes\cdots\otimes e_{i_k}\otimes f^{j_1}\otimes\cdots\otimes f^{j_l}\right)
\end{aligned}
$$

なので（添え字が大変！）, 両辺の成分を比較して

$$
\begin{aligned}
& T^{i_1\cdots i_k}_{j_1\cdots j_l}=\overline{T}^{a_1\cdots a_k}_{b_1\cdots b_l}A^{i_1}_{a_1}\cdots A^{i_k}_{a_1}\left(A^{-1}\right)^{b_1}_{j_1}\cdots\left(A^{-1}\right)^{b_l}_{j_l} \\
\iff & \overline{T}^{a_1\cdots a_k}_{b_1\cdots b_l}=\left(A^{-1}\right)^{a_1}_{i_1}\cdots \left(A^{-1}\right)^{a_k}_{i_k}A^{j_1}_{b_1}\cdots A^{j_l}_{b_l}T^{i_1\cdots i_k}_{j_1\cdots j_l}
\end{aligned}
$$

となり, やはり変換性が再現できました！物理の本はこの最後の式でテンソルを定義することが多いので, 一発でこの定義の意味を理解しろと言われても不可能だと思います. しかし数学的にはこの変換性はベクトル空間の基底変換の結果でしかないのです.

多重線形写像としてのテンソル

　結びに「テンソルは多重線形写像とみなせる」という事実を説明しておきます.

　共変ベクトルのところで説明しましたが, 共変ベクトルとは$${V^*}$$の元であり, $${V^*}$$とは$${V}$$から$${\mathbb{R}}$$への線形写像全体の集合でした. これを拡張して$${\left(0,l\right)}$$テンソル（$${l}$$階共変テンソル）$${T_1\otimes\cdots\otimes T_l\in\bigotimes^lV^*}$$は多重線形写像$${\underbrace{V\times\cdots\times V}_{l}\rightarrow\mathbb{R}}$$とみなせます.

　具体的には

$$
T_1\otimes\cdots\otimes T_l\left(v_1,\cdots,v_l\right)\coloneqq T_1\left(v_1\right)\cdots T_l\left(v_l\right)
$$

と定義するのです.

　同じことを反変テンソルの場合にも考えてあげましょう. 反変ベクトルも視点を変えれば線形写像$${V^*\rightarrow\mathbb{R}}$$と思えます. 具体的には

$$
v\left(T\right)\coloneqq T\left(v\right)\qquad\left(v\in V,T\in V^*\right)
$$

です（数学的に厳密に定義するには二重双対空間という概念を用います）. これを$${\left(k,0\right)}$$テンソル（$${k}$$階反変テンソル）に拡張すると, 多重線形写像$${v_1\otimes\cdots\otimes v_k: \underbrace{V^*\times\cdots\times V^*}_{k}\rightarrow\mathbb{R}}$$が

$$
v_1\otimes\cdots\otimes v_k\left(T_1,\cdots,T_k\right)\coloneqq T_1\left(v_1\right)\cdots T_k\left(v_k\right)
$$

と定義できます. 一般の$${\left(k,l\right)}$$テンソルに対しては, 多重線形写像$${v_1\otimes\cdots\otimes v_k\otimes T_1\otimes\cdots\otimes T_l:\underbrace{V^*\times\cdots\times V^*}_{k}\times\underbrace{V\times\cdots\times V}_{l}\rightarrow\mathbb{R}}$$が

$$
v_1\otimes\cdots\otimes v_k\otimes T_1\otimes\cdots\otimes T_l\left(U_1,\cdots,U_k,w_1,\cdots,w_l\right)\coloneqq U_1\left(v_1\right)\cdots U_k\left(v_k\right)T_1\left(w_1\right)\cdots T_l\left(w_l\right)
$$

と定められます.

テンソルの例: Minkowski計量 in 特殊相対論

　もっとも重要なテンソルの例は$${V=\mathbb{R}^{1,3}}$$（Minkowski時空）における$${2}$$階共変テンソルであるMinkowski計量（Minkowski metric）$${\eta:V\times V\rightarrow\mathbb{R}}$$でしょう.

　$${V=\mathbb{R}^{1,3}}$$の基底を

$$
e_0=\left(\begin{matrix}1 \\ 0 \\ 0 \\ 0\end{matrix}\right) e_1=\left(\begin{matrix}0 \\ 1 \\ 0 \\ 0\end{matrix}\right)
e_2=\left(\begin{matrix}0 \\ 0 \\ 1 \\ 0\end{matrix}\right)
e_3=\left(\begin{matrix}0 \\ 0 \\ 0 \\ 1\end{matrix}\right)
$$

にとったときの双対基底$${f^0,f^1,f^2,f^3}$$に対して, Minkowski計量は

$$
\eta=\eta_{\mu\nu}f^{\mu}\otimes f^{\nu}
$$

で与えられます. ただし

$$
\left(\eta_{\mu\nu}\right)_{0\leq\mu,\nu\leq 3}=\left(\begin{matrix}-1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{matrix}\right)
$$

はMinkowski行列です. つまり

$$
\eta=-f^0\otimes f^0+f^1\otimes f^1+f^2\otimes f^2+f^3\otimes f^3
$$

となります. このとき$${u=u^{\alpha}e_{\alpha}=\left(u^0,u^1,u^2,u^3\right)^T,v=v^{\beta}e_{\beta}=\left(v^0,v^1,v^2,v^3\right)^T\in V}$$に対し,

$$
\begin{aligned}
\eta\left(u,v\right) & =\eta_{\mu\nu}f^{\mu}\otimes f^{\nu}\left(u^{\alpha}e_{\alpha},v^{\beta}v_{\beta}\right) \\
& =\eta_{\mu\nu}u^{\alpha}v^{\beta}f^{\mu}\left(e_{\alpha}\right)f^{\nu}\left(e_{\beta}\right) \\
& =\eta_{\mu\nu}u^{\alpha}v^{\beta}\delta^{\mu}_{\alpha}\delta^{\nu}_{\beta} \\
& =\eta_{\mu\nu}u^{\mu}v^{\nu} \\
& =-u^0v^0+u^1v^1+u^2v^2+u^3v^3
\end{aligned}
$$

となって$${u}$$と$${v}$$のMinkowski内積が再現されました.

Minkowski計量による添え字の上げ下げ

　Minkowski計量$${\eta}$$を使って"添え字の上げ下げ"を説明してみましょう。物理の本では, 添え字が上付きの反変ベクトル（の成分）と下付きの共変ベクトル（の成分）はMinkowski計量（の成分）$${\eta_{\mu\nu}}$$で移り変われる, すなわち

$$
{v_{\mu}=\eta_{\mu\nu}v^{\nu}}
$$

と説明されていることが多いですが, そのカラクリは次の通りです.

　Minkowski計量$${\eta\left(\cdot\ ,\ \cdot\right):V\times V\rightarrow\mathbb{R}}$$は引数を2つとる写像ですが, あえて1つだけにしてみましょう. すると

$$
\begin{aligned}
\eta\left(\cdot\ ,v\right) & =\eta_{\mu\nu}f^{\mu}\otimes f^{\nu}\left(\cdot\ ,v\right) \\
& =\eta_{\mu\nu}f^{\nu}\left(v\right) f^{\mu} \\
& =\eta_{\mu\nu}v^{\alpha}f^{\nu}\left(e_{\alpha}\right)f^{\mu} \\
& =\eta_{\mu\nu}v^{\alpha} \delta^{\nu}_{\alpha}f^{\mu} \\
& =\eta_{\mu\nu}v^{\nu}f^{\mu} \\
& =v_{\mu}f^{\mu} & \left({v_{\mu}\coloneqq\eta_{\mu\nu}v^{\nu}}\right)
\end{aligned}
$$

のように2つの$${f^{\mu}, f^{\nu}}$$のうち1つだけが$${v\in V}$$によって潰されて, 反変ベクトル$${v=v^{\mu}e_{\mu}\in V}$$から共変ベクトル$${\eta\left(\cdot\ ,v\right)=v_{\mu}f^{\mu} \in V^*}$$を作り出せたことになります. その成分として$${v_{\mu}\coloneqq\eta_{\mu\nu}v^{\nu}}$$が定義されるのです.

　以上をすっきりまとめると次のように説明できます. Minkowski計量$${\eta}$$は2階共変テンソルなので本来は多重線形写像$${\eta:V\times V\rightarrow\mathbb{R}}$$ですが, 引数を1つにすることで$${\eta:V\rightarrow V^*}$$ともみなせるのです. 「添え字の上げ下げ」とは$${V}$$の元を$${V^*}$$の元に写す写像のことだったのです.

最後に

まとめ
反変ベクトル: ベクトル空間の元
共変ベクトル: 双対ベクトル空間の元
テンソル: ベクトル空間と双対ベクトル空間いくつかのテンソル積空間の元

　物理学者というのはアイデアを出すのが上手な人たちなのですが, どうも出したアイデアを方々に飛散させたまま放置する傾向が強いように思います. 数学者は雑多な概念を簡潔にまとめ直すのが得意ですから, 物理的対象を数学者の流儀で眺め直すのは知識を体系化する上で非常に役に立ちます.

参考文献

[1] 新井朝雄.『相対性理論の数理』. 日本評論社. 2021
[2] 雪江明彦.『代数学2 環と体とガロア理論』. 日本評論社. 2010