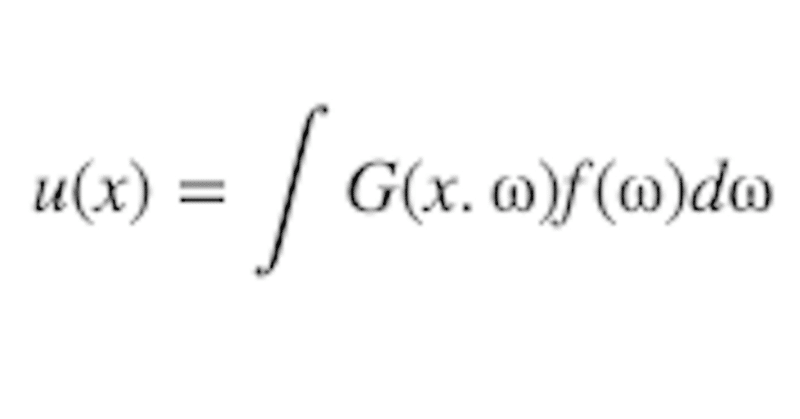
Green関数の入門的な話
Introduction
Green関数は微分方程式の解を求めるときに重要な役割を果たします。Lをなんらかの微分作用素として
Lu(x) = f(x), x ∈ Ω (*)
という微分方程式に興味があるとしましょう。ここで、集合Ωは実数空間の部分集合です。集合Ω上のある点ωを固定したとき、以下の方程式の解G(x,ω)を微分方程式(*)のGreen関数と言います*1。
LG(x, ω) = δ(x-ω)
ここで、関数δはDiracのdelta関数です。このノートでは、なぜGreen関数なんてものを考えるのかを説明します。
1. Green関数で微分方程式が解ける?
実は、微分方程式Lu(x)=f(x)に対してGreen関数G(x,ω)を求めることができれば、その微分方程式の解は
u(x) = ∫G(x, ω)f(ω)dω
によって求められることが期待できます*2。ここでは、その理由を大雑把に説明しましょう。

これがGreen関数を考えることで微分方程式の解が得られると期待する理由の(大雑把な)説明です。
2. 非斉次な常微分方程式を解く方法として
実際に、斉次な場合に簡単に一般解が求められる微分方程式なら、Green関数を用いることで非斉次な場合でも解を求められることが知られています。この話をもう少し正確に説明しましょう。難しく感じられる方は、第3節に例題も用意したので見比べてみてください。

この定理の性質1は、Green関数の定義から直ちに従うので考えてみてください。
ちなみに、境界条件にはよくDirichlet境界条件 u(a)=0, u(b)=0 とNeumann境界条件 u′(a)=0, u′(b)=0 が設定されます。今回はDirichlet境界条件の設定で定理を紹介しましたが、Neumann境界条件でもほとんど同様の定理が成り立つことが知られています。
3. Green関数で微分方程式の解を求めてみよう
せっかくなので、前節の定理を用いてGreen関数というアイディアを用いて、実際に微分方程式をひとつ解いてみましょう。 p(x)=1, q(x)=1, f(x)=x という最も簡単なSturm-Liouville作用素による微分方程式の例を考察します。

以下が解答例になります。楽しいので、みなさんもぜひ一度計算してみてください。

4. おわりに
このノートでは、Green関数のごく入門的な話を紹介してみました。実はGreen関数は、常微分方程式に限らず
・偏微分方程式の求解
・物理学
とも縁の深い対象で、特に量子力学では経路積分によってGreen関数を求める方法も知られています。またの機会により詳細な説明をしましょう。
Remarks:
*1:本来は作用素LのGreen関数というのですが、細かい話は良いことにしましょう。
*2:(Gf)(x) := ∫G(x, ω)f(ω)dωを一般に積分作用素といって、G(x, ω)をその積分核と呼んだりします。
サポートをいただいた場合、新たに記事を書く際に勉強する書籍や筆記用具などを買うお金に使おうと思いますm(_ _)m
