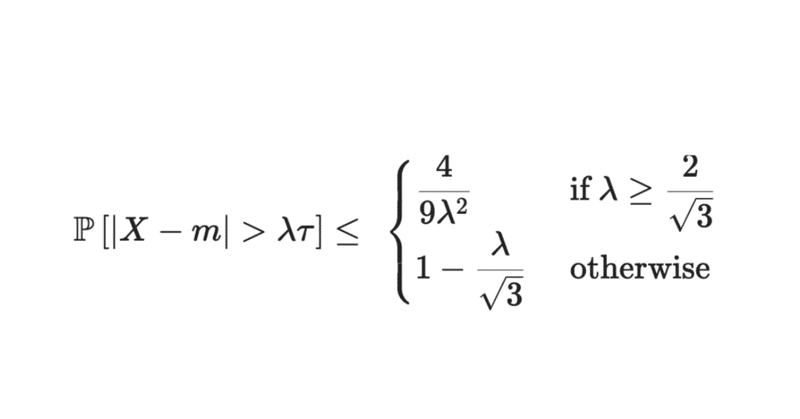
Gaussの不等式

abstract　Gaussの不等式は、単峰性を満たす確率分布の「裾確率」に対して上限を与える不等式の一つです。同様のものにChebyshevの不等式がありますが、Gaussの不等式では「単峰性」という強い仮定を確率分布に敷くかわりに、厳しい上限の評価を与えることができます。この記事では、Gaussの不等式とはなにかを詳しく説明し、その証明を与えます。

1　Introduction

1.1　確率分布の単峰性の定義の確認

「単峰性」とは、確率密度関数のグラフをかいたとき、山がひとつだけに見える様子を指す言葉です。例えば、正規分布は単峰性を満たしますが、混合正規分布は単峰性を持ちません。今回は、単峰性を以下のように定義します。

定義　確率分布が確率密度関数 $${f(x)}$$ によって定義されるとする。この関数 $${f(x)}$$ のグラフをかいたとき、点 $${m}$$ より左の範囲 $${x\leq m}$$ では単調増加し、点 $${m}$$ より右の範囲 $${x\geq m}$$ では単調減少するような点 $${x=m}$$ が存在するなら、この確率分布は単峰性を持つといい、点 $${x=m}$$ を最頻値という。■

Fig 1. 単峰性のイメージ

細かい注意ですが、今回の単調増加という言葉は $${x\leq y}$$ なら $${f(x)\leq f(y)}$$ という意味で用いています。平たく言えば、$${x}$$ 軸の値が増えたとき、関数の値が増えるか一定かのいずれかです。単調非減少と言ったほうが、しっくりくる方もいるでしょうか。

この注意から、単峰性を持つ確率分布の重要な例として、正規分布のほかに一様分布を挙げることができます。一様分布の場合、どの点も最頻値として選ぶことができ、最頻値より左の範囲では一定なので単調増加、最頻値より右の範囲でも一定なので単調減少しています。

1.2　Gaussの不等式の主張の紹介

1823年、ドイツの有名な数学者C. F. Gaussは、単峰性を持つ確率分布について、最頻値から一定以上離れた値が得られる確率の上限を評価した結果を示しました。これがGaussの不等式です。

定理　確率変数 $${X}$$ を単峰性を持つ確率分布に従うとします。そして、最頻値のうちの一つを選び $${m}$$ と表し、最頻値まわりの2次モーメントを $${\tau^2=\mathbb{E}[(X-m)^2]}$$ と表すことにします。このとき、

$$
\displaystyle\mathbb{P}\left[|X-m| > \lambda\tau\right] \leq \begin{cases}
\displaystyle\frac{4}{9\lambda^2}&\text{ if }\displaystyle\lambda\geq \frac{2}{\sqrt{3}}\\
\displaystyle1-\frac{\lambda}{\sqrt{3}}&\text{ otherwise }
\end{cases}
$$

が成り立つ。■

主張の意味を汲み取ることが難しいと感じる方もいるでしょう。1.3節では、Gaussの不等式がどうして興味深いのか、その意味を説明します。

1.3　Gaussの不等式の意味をおさえよう

分かりやすくするために、正規分布や一様分布のように、期待値を持ち、確率密度関数のグラフが期待値で左右対称なグラフをもつような確率分布に考察対象を絞ってみましょう。このとき、最頻値 $${m}$$ には期待値 $${\mu}$$ を選ぶことができます。また、最頻値まわりの2次モーメント $${\tau^2}$$ は分散 $${\sigma^2=\mathbb{E}[(X-\mu)^2]}$$と読み替えることができます。

このような確率分布に対して、Gaussの不等式の左辺は

$$
\mathbb{P}\left[|X-m| > \lambda\tau\right] = \mathbb{P}[|X-\mu|>\lambda\sigma]
$$

言葉で説明すると「期待値から標準偏差 $${\lambda}$$ 個分超える値が得られる確率」と読めるのです。Gaussの不等式は $${\lambda}$$ に具体的な値 $${\lambda=1,2,3}$$ を代入することで、

• 期待値±1標準偏差を超える値が得られる確率は最大で $${1-\displaystyle\frac{1}{\sqrt{3}}\sim42.3\%}$$

• 期待値±2標準偏差を超える値が得られる確率は最大で $${\displaystyle\frac{1}{9}\sim11.1\%}$$

• 期待値±3標準偏差を超える値が得られる確率は最大で $${\displaystyle\frac{4}{81}\sim4.9\%}$$

であることを教えてくれます。

2　関連する不等式

2.1　キーワードは裾確率

Gaussの不等式は、いわゆる「裾確率」の上限を評価した式です。裾確率とは、大雑把に言うなら「確率密度関数のグラフのうち左、右、または左右両方が占める確率」です。

Fig 2. 裾確率のイメージ

2.2　Chebyshevの不等式との比較

Gaussの不等式と同様に、裾確率の上限を評価したものにChebyshevの不等式があります。Chebyshevの不等式は、1867年にロシアの数学者P. Chebyshevによって証明が与えられた不等式です。

定理　確率変数 $${X}$$ は期待値 $${\mu}$$ と分散 $${\sigma^2}$$ をもつ確率分布に従うとします。このとき、

$$
\displaystyle\mathbb{P}\left[|X-\mu| > \lambda\sigma\right] \leq \frac{1}{\lambda^2}
$$

が成り立つ。■

Chebyshevの不等式は $${\lambda}$$ に具体的な値 $${\lambda=2,3}$$ を代入することで、

• 期待値±2標準偏差を超える値が得られる確率は最大で $${\displaystyle\frac{1}{4}\sim25.0\%}$$

• 期待値±3標準偏差を超える値が得られる確率は最大で $${\displaystyle\frac{1}{9}\sim11.1\%}$$

であることを教えてくれます。なお、$${\lambda=1}$$の場合には面白くない結果が返ってきます。試してみてください。

さて、Gaussの不等式と結果を見比べると、2標準偏差の場合も、3標準偏差のも場合も、Chebyshevの不等式の方が緩い結果になっていることが確認できます。これは確率分布に敷いた仮定が関係しています。Chebyshevの不等式は「期待値と分散が存在する」という比較的緩い仮定を敷いています。一方、Gaussの不等式は「単峰性」という確率分布の形に関する強い仮定を敷くことで、より厳しい裾確率の上限の評価を与えたものだと解釈できます。

3　Gaussの不等式の証明

Gaussの不等式の証明は、以下に紹介するもの以外にも複数知られていますが、いずれも技巧的です。今回は、主にH. Cramerが考えた証明を紹介します。読んでいて難しかった場合、4.1節を参考にすると、理解のヒントが得られるかも知れません。

3.1　示すこと

新しく確率変数 $${Z=|X-m|}$$ を定義します。このとき$${\tau^2=\mathbb{E}[Z^2]}$$、示したいことを

$$
\displaystyle\mathbb{P}\left[Z>\lambda\tau\right] \leq  \begin{cases}
\displaystyle\frac{4}{9\lambda^2}&\text{ if }\displaystyle\lambda\geq \frac{2}{\sqrt{3}}\\
\displaystyle1-\frac{\lambda}{\sqrt{3}}&\text{ otherwise }
\end{cases}
$$

と書き換えることができます。特に、$${\lambda=c/\tau}$$ とおくことで示したい不等式を次のように書き換えることができます。

$$
\displaystyle\mathbb{P}\left[Z>c\right] \leq  \begin{cases}
\displaystyle\frac{4\tau^2}{9c^2}&\text{ if }\displaystyle c\geq \frac{2}{\sqrt{3}}\tau\\
\displaystyle1-\frac{c}{\sqrt{3}\tau}&\text{ otherwise }
\end{cases}
$$

3.2　片方の不等式だけ示せば十分 

実は以下の不等式が、どんな正の実数 $${c>0}$$ に対しても成り立つことを示せば十分です。

$$
\displaystyle\mathbb{P}\left[Z>c \right] \leq \frac{4\tau^2}{9c^2}
$$

$${Z}$$ の累積分布関数を $${F(z)}$$、確率密度関数を $${f(z)}$$ と表すことにします。左辺の関数 $${y=1-F(z)}$$ のグラフを考えてみましょう。導関数は $${(1-F(z))'=-f(z)}$$ は、単峰性から単調減少関数なので、関数 $${y=1-F(z)}$$ は凸関数になります。そして不等式 $${\displaystyle\mathbb{P}\left[Z>c \right] \leq \frac{4\tau^2}{9c^2}}$$ は、関数 $${y=4\tau^2/9z^2}$$ のグラフは必ず関数 $${y=1-F(z)}$$ のグラフの上に存在することを主張しています。以下はこの様子を図で表したものです。

Fig 3. より厳しい不等式の存在

すると、赤い曲線の接線のうち点 $${(0,1)}$$ を通る青い直線に注目することで、区間 $${(0, z^*]}$$ の範囲では不等式 $${\displaystyle\mathbb{P}\left[Z>c \right] \leq \frac{4\tau^2}{9c^2}}$$  より厳しい不等式を得られることがわかります。そこで、青い直線を求めてみましょう。 $${\displaystyle y = -\frac{a}{\tau}z+1}$$ と表しておきます。

赤い曲線 $${y=4\tau^2/9z^2}$$ と青い直線 $${\displaystyle y=-\frac{a}{\tau}z+1}$$ の高さの差を測る関数

$$
\displaystyle g(z) = \frac{4\tau^2}{9z^2} + \frac{a}{\tau}z - 1
$$

は最小値が $${0}$$ の関数になっています。$${a}$$ を $${z^*, \tau}$$ で表す式は、関数 $${g(z)}$$ の導関数によって $${g'(z^*)=0}$$ を満たし

$$
\displaystyle g'(z^*) = -\frac{8\tau^2}{9{z^*}^3} + \frac{a}{\tau}
$$

から、$${a = 8\tau^3/9{z^*}^3}$$ と表せることがわかります。また、最小値を与える点 $${z^*}$$ は、$${g(z^*)=0}$$ を満たすので

$$
\displaystyle g(z^*) = \frac{4\tau^2}{3{z^*}^2} - 1
$$

から $${\displaystyle c=\frac{2}{\sqrt{3}}\tau}$$ と表せることがわかります。すなわち、$${\displaystyle c < \frac{2}{\sqrt{3}}\tau}$$ の範囲では、より厳しい不等式

$$
\displaystyle \mathbb{P}\left[Z>c\right] \leq 1 - \frac{c}{\sqrt{3}\tau}
$$

が成り立つことがわかりました。

そこで3.3節以降では、不等式 $${\displaystyle\mathbb{P}\left[Z>c \right] \leq \frac{4\tau^2}{9c^2}}$$ を示すことに注力します。

3.3　Zが区間[0,d]上の一様分布に従う場合

事前準備として、確率変数 $${Z}$$ が区間 $${[0,d]}$$ 上の一様分布に従う場合を考えます。ここでの考察が一般の場合を証明するときに役に立ちます。この場合、示したい不等式をより具体的な式に書き換えることで、次を証明すればよいことがわかります。

$$
\displaystyle\int_{c}^{d}dz \leq \frac{4}{9c^2}\int_{0}^{d}z^2dz
$$

左辺は $${d-c}$$、右辺は $${\displaystyle\frac{4d^3}{27c^2}}$$ です。右辺と左辺を引くと、

$$
\begin{align*}
\displaystyle \frac{4d^3}{27c^2}-(d-c) &= \frac{4d^3-27dc^2+27c^3}{27c^2}\\
&= \displaystyle\frac{4\left(d+3c \right)\left(d^2-3cd+9c^2/4\right)}{27c^2}\\
&= \displaystyle\frac{4\left(d+3c \right)\left(d-3c/2\right)^2}{27c^2}\\
& \geq 0
\end{align*}
$$

が得られるので、不等式が成り立つことを確認できました。

3.4　一般の場合

以下、$${Z}$$ の確率密度関数を $${f(z)}$$ と表すことにします。また、

$$
\displaystyle d = c + \frac{1}{f(c)}\int_{c}^{\infty}f(z)dz
$$

とおきます。すると、3.3節で示したことを用いて、

$$
\begin{align*}
\mathbb{P}\left[Z>c\right] &= \displaystyle\int_{c}^{\infty}f(z)dz\\
&= f(c)(d-c)\\
&\leq \frac{4}{9c^2}f(c)\int_{0}^{d}z^2dz
\end{align*}
$$

が得られます。あとは、$${\displaystyle f(c)\int_{0}^{d}z^2dz\leq \int_0^{\infty}z^2f(z)dz=\tau^2}$$ を示すだけです。確率密度関数 $${f(z)}$$ が単調減少であることに注意すると、

$$
\begin{align*}
\displaystyle f(c)\int_{0}^{d}z^2dz  &\leq f(c)\int_{0}^{c}z^2fdz + \int_{c}^{d}z^2(f(c)-f(z))dz + \int_{c}^{d} z^2f(z)dz\\
&\leq \int_{0}^{c}z^2f(z)fdz  + \int_{c}^{d}z^2(f(c)-f(z))dz + \int_{c}^{d} z^2f(z)dz\\
&\leq \int_{0}^{d}z^2f(z)fdz + \int_{c}^{d}z^2(f(c)-f(z))dz\\
\end{align*}
$$

が得られます。さらに、$${c \leq d}$$ および $${\displaystyle d = c + \frac{1}{f(c)}\int_{c}^{\infty}f(z)dz}$$ に注意して計算を進めると、

$$
\begin{align*}
\displaystyle \int_{c}^{d}z^2(f(c)-f(z))dz &\leq d^2\int_c^d(f(c)-f(z))dz\\
&= d^2\left(f(c)(d-c) - \int_{c}^{d}f(z)dz\right)\\
&= d^2\left(\int_{c}^{\infty}f(z)dz - \int_{c}^{d}f(z)dz\right)\\
&=  d^2\int_{d}^{\infty}f(z)dz\\
&\leq \int_{d}^{\infty}z^2f(z)dz
\end{align*}
$$

が得られるので、結果 $${\displaystyle f(c)\int_{0}^{d}z^2dz\leq \int_0^{\infty}z^2f(z)dz=\tau^2}$$ を示すことができました。以上で、示したい不等式が成り立っていることを確認できました。

4　Gaussの不等式はsharpか？

Gaussの不等式は「sharp」な不等式です。今回の場合、sharpな不等式とは等号が成立するような確率分布が存在することを意味しています。2つのケースを考えてみます。

4.1　一様分布の場合

確率変数 $${X}$$ が区間 $${[-1, 1]}$$ 上の一様分布に従うとして、最頻値 $${m=0}$$ を選択した場合を考えてみましょう。このとき、

$$
\displaystyle \tau^2 = \int_{-1}^{1}\frac{1}{2}z^2dz = \frac{1}{3}
$$

であることに注意します。

裾確率は次のように計算できます。

$$
\displaystyle \mathbb{P}\left[|X| > \sqrt{\frac{1}{3}}\lambda\right] = 1-\int_{-\sqrt{1/3}\lambda}^{\sqrt{1/3}\lambda}\frac{1}{2}dz = 1-\frac{\lambda}{\sqrt{3}}
$$

これは、$${\displaystyle\mathbb{P}\left[|X-m| > \lambda\tau\right] \leq 1-\frac{\lambda}{\sqrt{3}}}$$ の等号が成立している例です。

4.2　期待値に確率が集中している左右対称な分布の場合

確率変数 $${X}$$ が $${\mathbb{P}[X=0]=1-4/3\lambda^2}$$ かつ $${X\neq 0}$$ では区間 $${[-3\lambda/2, 3\lambda/2]}$$ の一様分布に従う場合を考えてみましょう。なお、この分布の最頻値は $${0}$$、一様分布の確率密度は $${\displaystyle\frac{4}{9\lambda^3}}$$ であることに注意します。まず、$${\tau^2}$$ は

$$
\begin{align*}
\displaystyle\tau^2 &= 0^2\times\mathbb{P}[X=0] + \frac{4}{9\lambda^3} \int_{-3\lambda/2}^{3\lambda/2}x^2dx\\
&= 1
\end{align*}
$$

と計算できます。そこで、Gaussの不等式の左辺を計算すると

$$
\begin{align*}
\displaystyle \mathbb{P}[|X|> \lambda] &= 2\times\frac{4}{9\lambda^3}\left(\frac{3\lambda}{2}-\lambda\right)\\
&= \frac{4}{9\lambda^2}
\end{align*}
$$

これは、$${\displaystyle\mathbb{P}\left[|X-m| > \lambda\tau\right] \leq \frac{4}{9\lambda^2}}$$ の等号が成立している例です。

5　発展的な話題の紹介

Gaussの不等式の証明は、今回紹介したもの以外にもいくつか知られています。Gaussが最初に与えた証明は座標幾何的で、初等的ですが興味深いものになっています。またKhintchine表現とJensenの不等式を用いた証明では、不等式がsharpであることを示す例まで難しくなく構成できます。

Gaussの不等式には、Vysochanskij-Petuninの不等式とよばれる一般化が存在します。この不等式では、単峰性の仮定はそのままに、最頻値をより一般の点に置き換えた場合の裾確率の上限の評価が与えられます。

これらの話についても、また後日説明できるとよいですね。

Reference

[C] Cramer, H. (1946). Mathematical Methods of Statistics. Princeton, NJ: Princeton University Press.
[G] Gauss, C. F. (1821). Theoria Combinationis Observationum Erroribus Minimis Obnoxiae, Pars Prior. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores 5, Also in Werke, Band 4, 1–93.
[P] Pukelsheim, F. (1994). The Three Sigma Rule. American Statistician, 48 (2): 88–91.

Acknowledgement　この頃、気分が沈み気味の自分に対して、温かい声をかけてくださった周囲の方々に心から感謝しています。この記事は文章を書くリハビリを兼ねて書いたものです。少しずつ調子を取り戻しながら、色々な活動を再開できるよう頑張っていきます。