
動かして学ぶバイオメカニクス #29 〜ヤコビ行列#3
ヤコビ行列はたとえば手先の位置と関節角度の関係を記述する多変数ベクトル関数の微分から数学的に導かれることをこれまでに示してきた.これは手先と関節間の速度関係(微分運動学)を記述するが,それだけでなく,手先に作用する力と関節に作用するトルク間の釣り合い示すの静力学関係も記述する.この手先空間と関節空間の関係を運動学と力学の両方で記述できるこのヤコビ行列はきわめて有用で,全身運動を直感的に理解する上でも重要なツールとなる.このことを理解するために,もうしばらく複数の章を記述することをお許しいただきたい.
はじめに
ヒトの運動パターン形成はエンドエフェクタで拘束される
多くの身体運動では,まず手先や足先の位置が拘束され,それに従って身体の運動が定まる.ロボットでは手先や足先に相当するのがエンドエフェクタ(end effector,手先効果器)で,便利な用語なので今後も時々使用する.

スポーツに限らず多くの身体運動では,このような末端での拘束が強く作用し,特にその末端での運動学的・力学的拘束がなによりも最上位で我々の運動パターンを拘束していることを強く意識すべきだろう.神経科学的な都合や生理学的な都合ではなく,力学的な都合が優先され運動パターン形成が実現されることがほとんどだ.
コップを移動させるリーチング運動であれば,手の位置と姿勢の運動学的拘束を保つように動かさなければこぼれてしまう.投球であればボール作用する力とトルクの力学的拘束が,ボールの制御を拘束する.それを怠ればあらぬ方向に飛んでいく.キック動作もボールと足の接触は一瞬だが,そのキックの瞬間の力学問題を制御するように,身体の動かし方が定まる.ランニングなら転ばぬように地面を蹴ることで身体重心を制御している.立ったり座ったりする運動でも同様だ.当たり前のことだが,「運動の目的」が,所望の手先・足先の運動や力の発揮の仕方を「最初に」「強く」拘束し,それを身体全体に分配させたり,手先・足先と身体各部位間で協調しながら身体運動を制御するという構図が必ずあることを無視してはいけない.それを無視し身体運動の解析や制御を考えてしまえば,もやはそれは身体運動にはならない.もちろん,肘や膝が最初に拘束されることもあるだろう,おしりでドアを閉めることもあるが,そのときでもおしりを手先のかわりに同じように考えれば良いだけのことだ.
このことから,手先や足先と道具などの環境(たとえば,ボールや地面)間との力学を正しく理解せずに,身体の動かし方を理解しようとすることは,誤った理解を導く可能性があることを示している.たとえば.速く走るために鉛直方向の床反力を大きくしても意味はなく,重要なのはあくまでも水平方向の力であることすら,意識をしていない方も多いかもしれない.水平力は鉛直方向の力間には,力学的な拘束があり,離地する必然性や水平力を大きくするためには鉛直方向の力は必要だが,走速度を最終的に規定するのはあくまでも水平方向の力である.
また,肩のトルク発揮を増大させることができれば,より速い球を投げることはできるだろう.ヒトが実際に投げるときは所望の運動を実現するために,必ずエンドエフェクタと間接間の協調しながら投げてくれる.しかし,全く同じようなトルクパターンを発揮してはいては,外乱や環境の変化に適応して投げることはできない.変化に適応することを数学的にトルクを定めることはそれほど単純な問題ではなく,ボールが正しい方向に飛翔するようにエンドエフェクタと各関節間の数学的関係を満たすように,肩関節のトルクを計算する必要がある.単純に肩関節のトルクを増やしても,ボールが良からぬ方向に飛んでいくどころかその場にボールが虚しく落ちてしまうだろう.ボールの制御は実に精巧な制御を行わないと実現できない.
ただし,末端から身体方向だけでなく,同時に身体重心と末端間との協調も行った上で運動は成り立っている.両方だが,今回は運動の目的が「先ず」末端が拘束する力学を意識していただきたい.
その手先の拘束を考えずに身体の動かし方を論じても,「たまたま」なりっているだけかもしれないと危惧したほうがよい.実験データは必ずそのような制御をヒトが行っているうえでの結果であることを多くの人はあまり意識していない.
しかし,シミュレーションを行えば,この現実に直面することができる.例えばハンマー投競技における,ハンマーだけでも,実際のハンマーの挙動と同じような運動を自律的に動かせるような制御ルールを構築することは,それほど簡単な問題ではない.ましてやヒトのようにボールを投げるロボットをつくることは現在の技術では難しい.ロボットっぽい投球ロボットならいくらでもあるが...ご興味のある運動でどうやってシミュレーションができるか制御ルールを一度考えてみるとよいだろう.座位から立位への運動,立っている姿勢から,前後左右への一歩の移動ですら,自然なヒトらしい運動を追求するとそれほど単純な制御ではない.そのためにCOPと重心間の関係がどうあるべきか考えてみるとよいだろう.ある力学や運動学関係を満たさない限りは,絶対,移動や立つことなどできない.
野球の投球におけるボールの力学がどのように全身の運動を拘束するかについては,どこかで詳しく述べる予定だ.
そのような末端での拘束など気にせずに研究をすることが多いが,つねにエンドエフェクタの力学が,全身の力学を拘束することを強く意識すべきだ.そのメカニズムがよく解明されている運動もあるだろうが,多くの運動でその解明はほったらかしのままである.解明されていても,それを認知せず,意識せずにいることも多いだろう.まずはその末端の力学を明らかにしてから,運動に携わる研究を行うものは研究を行うべきと筆者は強く感じる.
冒頭から脱線してしまった.思想ばかり述べていると揶揄される機会が多いが,お許しいただきたい.
力学計算におけるヤコビ行列の役割
このような観点からも,身体運動の解析において,手先と関節間の速度レベルでの運動の変換は重要な役割を果たす.ヤコビ行列(Jacobian matrix)はこの手先と関節間の関係を結びつける重要なツールとなる.研究者のみならず,理学療法やトレーナーの方々にとっても間違いなく直感的な理解の助けとなる.
ヤコビ行列はエンドエフェクタと関節間の関係だけを記述するためにあるのではなく,身体各部と身体重心間の関係を重心ヤコビ行列で記述しても良い.ただし,ここでは先ずエンドエフェクタと各関節間の関係に注目する.
前章
でも示したようにヤコビ行列は,もともとは数学的に多変数ベクトル関数(たとえば関節の角度$${\bm{q}}$$などの関数)を微分することで導出され,手先位置$${\dot{\bm{x}}}$$と関節$${\dot{\bm{q}}}$$間の速度関係を記述する関数行列である.たとえば,前章で示したように平面2リンク機構であれば
$$
\begin{aligned}
\bm{x} &= \bm{\Psi}(\bm{q})=
\begin{bmatrix}
l_1 \cos q_1 + l_2 \cos(q_1 + q_2) \\
l_1 \sin q_1 + l_2 \sin(q_1 + q_2)
\end{bmatrix}
\\\\
\bm{J}(\bm{q}) &= \frac{\partial \bm{\Psi}}{\partial \bm{q}}=
\begin{bmatrix}
-l_1 \sin q_1 - l_2 \sin(q_1 + q_2) & -l_2 \sin(q_1 + q_2)\\
l_1 \cos q_1 + l_2 \cos(q_1 + q_2) & l_2 \cos(q_1 + q_2)
\end{bmatrix}
\\
\dot{\bm{x}} &= \bm{J}(\bm{q}) \dot{\bm{q}}
\end{aligned}
$$
と記述できるように,速度レベルで記述する微分運動学(differential kinematics)では行列で線形に記述できる.ただし,残念ながら位置や角度レベルでは,1行目の式のように非線形関数$${\bm{\Psi}}$$のままで記述することになり,これは計算上便利ではないことは前章で示したとおりである.
また,身体運動において(ロボットでも)ヤコビ行列は運動学にとどまらず,手先力と関節に作用するトルク間の力学関係を記述するツールとなる.このことは実用的にとても大きな意味を持ち有力であるので,この章では身体の静力学におけるヤコビ行列の意味を考える.
特に大きな外力が作用する部位近くに限定されるが,このことの意味を最初に簡潔に述べるならば面倒な動力学計算を行わずに,関節に作用するトルクの計算を,エンドエフェクタに作用する力ベクトルと姿勢だけを考えた静力学計算に落とし込むことができることを意味する.つまり関節に作用するトルクを計算するために,加速度やいわゆる力学計算や繰り返し計算などが不要となり,問題は極めて単純になる.
次に仮想仕事の原理から,手先力と関節力間の静力学関係をヤコビ行列で記述することを考える.
仮想仕事の原理
仮想仕事の原理(virtual work principle)は解析力学で学ぶ原理だ.古典力学の範疇を超え,抽象的でその意味がわかりにくいかもしれないが,身体の静力学関係を記述する上で重要な仮想仕事の原理について述べていく.なお,これは「原理(principle)」であるので,一般には導出することのできない理(ことわり)であり,物理現象の出発点の法則なので,なぜこれが成り立つのかを考えてはいけない.法則は原理から導くことができるが,原理は一般には証明できないものである(原理と呼ばれているものでも証明できるものもある).

仮想仕事の原理について述べる前に,まず釣り合いや平衡(equilibrium)について述べる.力学的な平衡とは運動状態が変化せず,物体に作用する力が釣り合っている状態をいう.静力学(statics)状態ともいえる.物体に$${n}$$個の力が作用しているとしよう.このとき作用する「全ての」力は釣り合っている.したがって,ニュートンの運動方程式,すなわち並進の運動だけ考えれば,
$$
\bm{f}_1 + \bm{f}_2 + \bm{f}_3 + \cdots +\bm{f}_n= \bm{0}
$$
と書くことができ,
$$
\sum_i^n \bm{f}_i = \bm{0}
$$
となる.反対に$${\sum_i^n \bm{f}_i \ne \bm{0}}$$となる場合は,平衡ではなく運動が発生し,動力学的状態と呼ぶ.
ここで,仮想変位(virtual displacement)を導入する.これがわかりにくさの原因だが,仮想変位はそもそも仮想なので,そのような物理量は計測することなどできなく,あくまでも想像上の変位である.
仮想変位$${\delta \bm{r}_i}$$は「力$${\bm{f}_i}$$ を変化させないような無限小の変位」として仮想的に考えたものである(図3).この記号$${\delta}$$は,微小なという意味だけではなく,仮想という意味が込めて$${d \bm{r}}$$と区別し,この無限の小ささを記号の$${\delta}$$で示し,ここでの仮想変位はベクトルで記述している.

次に,この仮想変位を利用し,仮想仕事(virtual work)を導入する.物体に力$${\bm{f}_i}$$が作用し,物体が$${\Delta \bm{r}_i}$$だけ移動すると仕事$${W = \bm{f}^T \Delta \bm{r}}$$が発生するが,仮想仕事$${\delta W}$$とは仮想変位$${\delta \bm{r}}$$によってなされる仕事で
$$
\bm{f}_i^T \delta \bm{r}_i
$$
を力$${\bm{f}_i}$$のなした仮想仕事とよび,仮想仕事の原理
$$
\begin{aligned}
\delta W &= \bm{f}_1^T \delta \bm{r}_1 + \bm{f}_2^T \delta \bm{r}_2 + \bm{f}_3^T \delta \bm{r}_3 + \cdots + \bm{f}_n^T \delta \bm{r}_n
\\
&= \sum_i^n \bm{f}_i^T \delta \bm{r}
\\
&= 0
\end{aligned}
$$
が成立する.つまり,平衡状態では,$${\sum_i^n \bm{f}_i = \bm{0}}$$であったが,仮想変位は力$${\bm{f}_i}$$ を変化させないような無限小の変位であるので,仮想仕事の和も零である.質点でも多リンク機構の多体系でも成り立つ.
力の釣り合いだけ述べたければ,すなわち平衡状態だけ述べたいなら,$${\sum_i^n \bm{f}_i = \bm{0}}$$と書けばすむが,これを仮想仕事にまで拡張して平衡状態を記述することで,内・外力の平衡のみならず,回転の仕事と並進の仕事も交えて記述できることが嬉しい.
ちなみに,ここでは詳しい説明は行わないが,内力は仕事に影響しない作用反作用の力で打ち消し合う力なので,結果考慮する必要はないということだけ補足しておく.したがって,ここでは内力は無視して図の赤色の力だけ考える.
力とモーメントの平衡も,力のモーメントを導入すれば一つの式に混在させて記述できるが,仮想仕事自体は各力の幾何学的な関係を導入せずに平衡状態を記述できるところが利点となる.複雑に力が作用するほど幾何学構造を考えなくて良い恩恵が得られる.といっても,平衡状態を仮想仕事で記述できるが,実際に問題を解く上では幾何学構造は必要となることにはかわりがない.それでも次の静力学問題を解く上で恩恵がある.以上をまとめると,
仮想仕事の原理は,
「内・外力の平衡(つり合っている)」=「仮想変位のする仕事の和がゼロ」
を示している.これだけだ.「平衡状態において」という前置きで,物体に作用する力とトルク(力のモーメント)をすべて考慮し,その力とトルクが行う仕事ではなく,仮想仕事を足し合わせれば0になる,ということを意味する.
次に,この原理を利用し,少し具体的に,身体の手先に作用する力と関節に作用するトルクの平衡を考える.
静力学関係
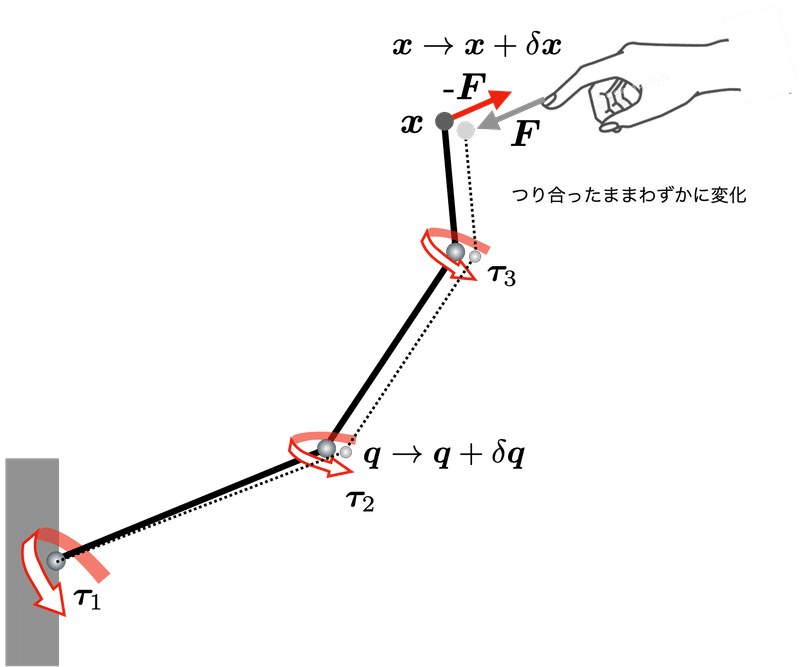
リンク機構を考え,手先(足先)に作用する力を$${\bm{F}}$$とし(ここでは単純化するため,手先にはトルクは作用しないとする)関節に作用するトルクを$${\bm{\tau}}$$とする.ここで,リンク系(腕などの多関節機構)が平衡状態,すなわち,力が釣り合い手先や関節が変化しない(動かない)状態にあるときの手先力$${\bm{F}}$$と関節力$${\bm{\tau}}$$の関係を,仮想仕事の原理から導出する.
リンク系に作用する全ての力とトルクの仮想仕事は
$$
\bm{F}^T \delta \bm{x} + \bm{\tau}^T \delta \bm{q} = 0
$$
と書くことができる.

たとえば,前章で述べた平面2リンク機構(図5)なら
$$
\begin{aligned}
\bm{F}& = [F_x~F_y]^T
\\
\bm{\tau} &= [\tau_1 ~ \tau_2]^T
\end{aligned}
$$
となる.仮想仕事の原理を記述する際には,$${\delta \bm{x}, \delta \bm{q}}$$という記号で記述する必要があったが,同様に微小な変位を$${d \bm{x}, d \bm{q}}$$と書けば,同様に
$$
\begin{aligned}
\bm{F}^T d \bm{x} + \bm{\tau}^T d \bm{q} &= 0
\\
[F_x~F_y]
\begin{bmatrix}
dx \\
dy
\end{bmatrix}
+
[\tau_1~\tau_2]
\begin{bmatrix}
dq_1 \\
d1_2
\end{bmatrix}
&= 0
\\
F_x dx + F_y dy + \tau_1 dq_1 + \tau_2 dq_2 &=0
\end{aligned}
$$
と書くことができる.ここで,さらに微小変位$${d \bm{x}, d \bm{q}}$$の間に前章
で述べたように,
$$
\begin{aligned}
\dot{\bm{x}} &=\bm{J}(\bm{q}) \dot{\bm{q}}
\\
\frac{d \bm{x}}{dt} &=\bm{J}(\bm{q}) \frac{d \bm{q}}{dt}
\\
d \bm{x} &=\bm{J}(\bm{q})~ d\bm{q}
\end{aligned}
$$
のようにヤコビ行列で記述できることを思い出せば,
$$
\begin{aligned}
\bm{F}^T d \bm{x} + \bm{\tau}^T d \bm{q} &= 0
\\
\bm{F}^T d \bm{x} &= - \bm{\tau}^T d \bm{q}
\\
\bm{F}^T \bm{J}(\bm{q})~ d\bm{q} &= - \bm{\tau}^T d \bm{q}
\\
\bm{F}^T \bm{J}(\bm{q}) &= - \bm{\tau}^T
\\
\bm{\tau}^T &= - \bm{F}^T \bm{J}(\bm{q})
\end{aligned}
$$
となる.ここで,両辺の転置をとると
$$
\bm{\tau} = - \bm{J}^T(\bm{q}) \bm{F}
$$
を得る.
また前章の結果から,平面2リンク機構のヤコビ行列は
$$
\bm{J} = \frac{\partial \bm{\Psi}}{\partial \bm{q}} =
\begin{bmatrix}
\frac{\partial \Psi_1}{\partial q_1} & \frac{\partial \Psi_1}{\partial q_2} \\
\frac{\partial \Psi_2}{\partial q_2} & \frac{\partial \Psi_2}{\partial q_2}
\end{bmatrix}
=
\begin{bmatrix}
-l_1 \sin q_1 - l_2 \sin(q_1 + q_2) & -l_2 \sin(q_1 + q_2)\\
l_1 \cos q_1 + l_2 \cos(q_1 + q_2) & l_2 \cos(q_1 + q_2)
\end{bmatrix}
$$
であったので,
$$
\begin{aligned}
\bm{\tau} &= - \bm{J}^T(\bm{q}) \bm{F}
\\
\begin{bmatrix} \tau_1 \\ \tau_2 \end{bmatrix} &= -
\begin{bmatrix}
-l_1 \sin q_1 - l_2 \sin(q_1 + q_2) & -l_2 \sin(q_1 + q_2)\\
l_1 \cos q_1 + l_2 \cos(q_1 + q_2) & l_2 \cos(q_1 + q_2)
\end{bmatrix}^T
\begin{bmatrix} F_x \\ F_y \end{bmatrix}
\\
&= -
\begin{bmatrix}
-l_1 \sin q_1 - l_2 \sin(q_1 + q_2) & l_1 \cos q_1 + l_2 \cos(q_1 + q_2)\\
-l_2 \sin(q_1 + q_2)& l_2 \cos(q_1 + q_2)
\end{bmatrix}^T
\begin{bmatrix} F_x \\ F_y \end{bmatrix}
\end{aligned}
$$
となる.つまり,図5のような姿勢$${\bm{q}=[q_1~q_2]^T}$$で,手先に力$${\bm{F}=[F_x~F_y]^T}$$が作用しているとき,対応する各関節に作用するトルク$${\bm{\tau}=[\tau_1~\tau_2]^T}$$がヤコビ行列の転置行列$${\bm{J}(\bm{q})^T}$$で定まる.
このように仮想仕事の原理を用いれば,手先と関節間の運動関係がヤコビ行列で記述できたように,手先力と関節に作用するトルク間の静力学関係もヤコビ行列で記述することができる.
これは平衡状態,すなわち力が釣り合った動かない状態で成り立つ式だ.しかし,もし運動が激しく加速度変化が大きくない場合は,動的な成分
$$
\bm{I}_{i} \dot{\bm{\omega}}_{i} + \bm{\omega}_{i} \times \bm{I_{i} \omega_{i}}
$$
の項がトルクよりも小さく無視できることがある.そのような場合は,
$$
\bm{\tau} \approx - \bm{J}^T(\bm{q}) \bm{F}
$$
の近似で計算されるということだけ予め述べておく.もし,これまで述べてきたような面倒な力学計算が,このような式だけで関節に作用するトルクを計算できるとしたら,動力学計算がどれだけ簡単な問題に落とし込められるかは,容易に想像できるはずだ.しかも姿勢から,作用するトルクの大きさもイメージできる.
このことを利用すれば,たとえば,足の姿勢$${\bm{q}}$$が既知で,足先に床反力$${\bm{F}}$$が作用するとき,膝関節に作用するトルクはヤコビ行列と床反力の積$${\bm{J}^T(\bm{q})\bm{F}}$$だけで膝関節に作用する静的なトルクが計算できる.ただし,ヤコビ行列のこの記述方法では三角関数を含んだ形式で記述されているため,このヤコビ行列の計算をイメージしにくいが,テコの原理をイメージできる形に変換することで,関節に作用するトルクを直感的に理解できる形式に変換するのが次章以降の目的となる.
ヤコビ行列はてこの行列である
このことから,ヤコビ行列は関節力を手先力に変換する,多次元で記述する「てこ」の役割を果たしている.もともと多変数ベクトル関数の微分から導出したヤコビ行列は,「てこ比の行列」に置き換えられることを予見している.もう少し別の言い方をすると「モーメントアームの行列」といえる.このことは,次章で明確になる.
冗長自由度
冗長自由度はバイオメカニクスではあまり議論の対象とはならないが,制御ではこれは切実な問題である.しかし,力学で考えたほうがスマートな解決につながるだろう.
逆運動学問題と静力学
$$
\dot{\bm{x}} = \bm{J}(\bm{q}) \dot{\bm{q}}
$$
この式の意味を考えてほしい.もし,手先・足先の自由度$${m}$$よりも関節の自由度$${n}$$が大きく冗長性があればヤコビ行列に「一般的な」逆行列は存在しない.これは手先速度を定めても一般解として一意に関節の速度定められないことを意味する.しかし,一般解が存在しないが,何らかの方法で逆行列を定めることはできる.
一方,手先力$${\bm{F}}$$と関節に作用する$${\bm{\tau}}$$間の静力学関係
$$
\bm{\tau} = - \bm{J}^T(\bm{q}) \bm{F}
$$
は,手先の力を定めれば,一意に対応する関節のトルクは定まる.つまり,静力学では手先空間から関節空間への写像において冗長性は存在しない.これは重要な知見である.ボールに作用する力が定まれば,その時の腕の姿勢で関節に作用するトルクは定まる.ただし,あくまでも動いていない平衡な条件のもとで成り立つことに注意されたい.
しかし,動的な成分と静的に定まる成分は,独立に定まるので,静的な力・トルク成分は動的な項と分離して計算することができる.別な言い方をするなら,手先(足先)に作用する力からトルクへの「分配」は一意に定まり,それは姿勢で定まることになる.しかも,もし動的な成分が小さい場合は,関節に作用するトルクは,手先や足先に作用する力(つまり床反力)と姿勢でほぼ近似的に定まる.(加速度が小さいという意味で動的に)動かないほど関節に作用するトルクと手先力は近似計算ができることになる.実際外力が大きいほど,そのようなことが身体運動では起きている.このことは具体的に,別途述べる.
一方で直感的には不思議なことに,姿勢を与えて関節に作用するトルクを一意に定めても,手先に作用する力を一意に決めることができないという問題が発生する.つまり,トルク(関節空間)から手先力(手先空間)に対しては冗長性が存在する事実にも注目すべきだろう.特にスポーツのような力の支配が優位な運動では,身体の動かし方は関節に作用するトルクで定まるといってもよいが,それは手先や足先の外力の与え方で支配されているということを意味する.
このように,運動学と静力学では手先空間と関節空間で,冗長性が発生するマッピングの方向が反対となっていることに注意していただきたい.
冗長自由度と運動学・静力学関係の数学的な整理

図6は$${n}$$次元空間の関節空間から$${m}$$次元の手先空間間の写像を,微分運動学(a)と静力学(b)の場合をそれぞれ示している.詳しくは文献1を参照されたい.
微分運動学の場合(図6(a)),もし前章で述べた特異姿勢でなければ,すなわちヤコビ行列の行列式(大きさ)が0でない姿勢$${\bm{q}}$$であれば,取りうるすべての関節速度$${\dot{\bm{q}}}$$の全集合(左の青太線の集合)は,右側の手先空間では青い破線の集合$${\dot{\bm{x}}}$$に変換され生成可能な手先速度の集合となり,常に存在する.
しかし,特異姿勢の場合,すなわち図6(a)の左側の関節空間のグレーの集合は,手先空間を覆うことができない(手先空間の黒丸に相当).これは線形代数における零空間(null space)または核(kernel)に相当し,$${\bm{J}}$$の零空間の関節速度$${\dot{\bm{q}}}$$は作業空間における手先速度を生成できず,特異姿勢でいくら動かしても手先は動かないことを示している.
一方,静力学(b)においてこの関係は全く反対になる.数学的にはこれは双対(dual)と呼ぶ.つまり,もし特異姿勢でなければ,取りうるすべての手先力$${\bm{F}}$$の全集合(右の赤太線の集合)は,左側の関節空間では青い破線の集合に変換され生成可能な関節に作用するトルク$${\bm{\tau}}$$の集合となり,常に存在する.
しかし,特異姿勢の場合,すなわち図6(b)の右側の関節空間のグレーの集合は,手先空間を覆うことができない(手先空間の黒丸に相当).たとえば上腕と前腕を一直線に伸展した状態では,腕の長軸に対して垂直な方向に手先で力を与えることができない.つまり$${\bm{J}^T}$$の零空間の手先力$${\bm{F}}$$は関節空間におけるトルク$${\bm{\tau}}$$を生成できず,特異姿勢では手先力につりあう関節に作用するトルクは存在しない(逆写像が存在しない)ことを意味している.
Motor control研究の文脈における冗長自由度
冒頭,運動は手先空間から関節空間方向に定まると述べた.写像で考えればマッピングの方向は図6の左から右方向に定まり,身体運動の行い方は運動学的だろうが力学だろうが,多くの場合その方向に定まる.しかし,所望のエンドエフェクタの位置を定めようとしても冗長自由度のために,姿勢を一意にさだめることができず,これを冗長自由度と呼んだ.
motor controlの研究ではこの冗長自由度の問題をBernstein問題という.そして,その自由度をいかに制御するかを協調(coordination)またはシナジー(synergy)と呼び,身体運動においてどの自由度を中心に運動を形成されているか基底を探るシナジー解析を行い,自由度を削減することが運動の協調の本質と考えている.
しかし少し視点を力学に変えると,手先空間と関節空間の冗長性は図6(b)に示したように存在しない.実際,1990年代に有名なBizziらのカエルを用いた研究では,脊髄のある部位を刺激すると,カエルの足先が初期値がどこにあって同じ終端位置に移動し,あたかもバネ(スティフネス)の平衡点が存在するような振る舞いを示すことを示している.しかも,このような平衡点のような終端値と刺激位置の対応は複数存在し,脊髄内の二つの部位を同時に刺激すると,その線形和の異なる位置に移動する(文献2などを参照).ヒトがこのような組み合わせで運動を制御しているかどうかはわからないが,少なくともカエルではすでに脊髄レベルで冗長性の問題は力学的に解決していることに注目すべきだろう.
Bizziらはこれをシナジーと呼んでいたが,いつのまにかシナジーは冗長自由度を機械学習によって少ない基底で表現する(低ランク近似)問題に置き換わってしまった.シナジー解析の研究は目立った成果を出さずに,つまりそれが本当に運動の本質であるかどうかの議論は行わずに,それが解析結果だけ示され,やまのように存在する.ただし,これ支持する議論と,支持しない議論は続いていることも申し添えておく.
おわりに
冒頭,「身体の末端の力学が,全身の力学を拘束することを強く意識すべき」と述べたが,幸いトレーナーや理学療法の現場では,幸いそのことは意識しなくても介入は成立する.なぜなら,その制御を実際に行っているヒトを相手に介入を行いるため,無茶な介入でない限り,介入の良し悪しにかかわらずヒトが上手に運動を成立させている.motor controlやバイオメカニクスの研究でも,そのことを度外視した解析を行うことがほとんどだ.たとえば投球速度と身体のなにかの変数や特徴量と統計的に結びつけるだけのロジックが主体だが,その制御が成り立っているヒトを相手に研究をしているので成立しているということをより強く意識すべきだろう.制御やシミュレーションなどを行う場合には,それを無視してはヒトらしい運動はもとより,タスクそのものを実現できない現実に直面する.研究者は,一度,運動の力学シミュレーションなどを行うとよいだろう.間違いなく,この問題を強く意識することになるはずだ.
次章について
ヤコビ行列がてこ比の行列であること述べたが,数学的にはモーメントアームの外積をまとめた行列を意味する.もちろんこのことは数値計算や解析でも有用だが,経験のあるトレーナーや理学療法士なら,姿勢を見ただけである程度,関節に作用するトルクの大小が予想できる利点をもたらす.たとえば,スクワットの姿勢の良し悪し,怪我のリスクなどが予見できる.正確に可視化するにはモーションキャプチャやモーションセンサなどが必要だろうが,そのようなものがなくても,計測道具なしに判断できる意義がある.つまり,フォームの良し悪しを,簡単に科学的な裏付けに基づいた評価が可能になる.
次章
では,多変数ベクトル関数の微分から導出したヤコビ行列を,外積で記述された形式に書き換えることを試みる.また,この章までは平面運動の例を扱ったが,3次元に拡張する.
参考文献
1)伊藤,身体知システム論(ヒューマンロボティクスによる運動の学習と制御),共立出版,2005
2)F A Mussa-Ivaldi, S F Giszter, and E Bizzi,Linear combinations of primitives in vertebrate motor control. Proc Natl Acad Sci U S A. 1994 Aug 2; 91(16): 7534–7538.



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
