忘れっぽい数学。線形代数のメモ
忘れっぽくて何度も調べなおして思い出す際にインターネットや本から検索するのがめんどくさいので、ここにあらかじめまとめておく。
線形代数について。
ここでは厳密な数学上の定義を示しているわけではない。
[用語]**行列
めっちゃ忘れる。
・変換行列
任意のベクトル空間でのある基底からある基底に変換する行列のこと
n次正方行列になり、正則になる。逆行列を持つ。(nは基底のベクトルの要素の数)
この逆行列が、逆向きに基底を変換する際に使える変換行列になる。
座標変換に使える。PやQで表されがち。
2次ベクトル空間場合は、以下のようになる
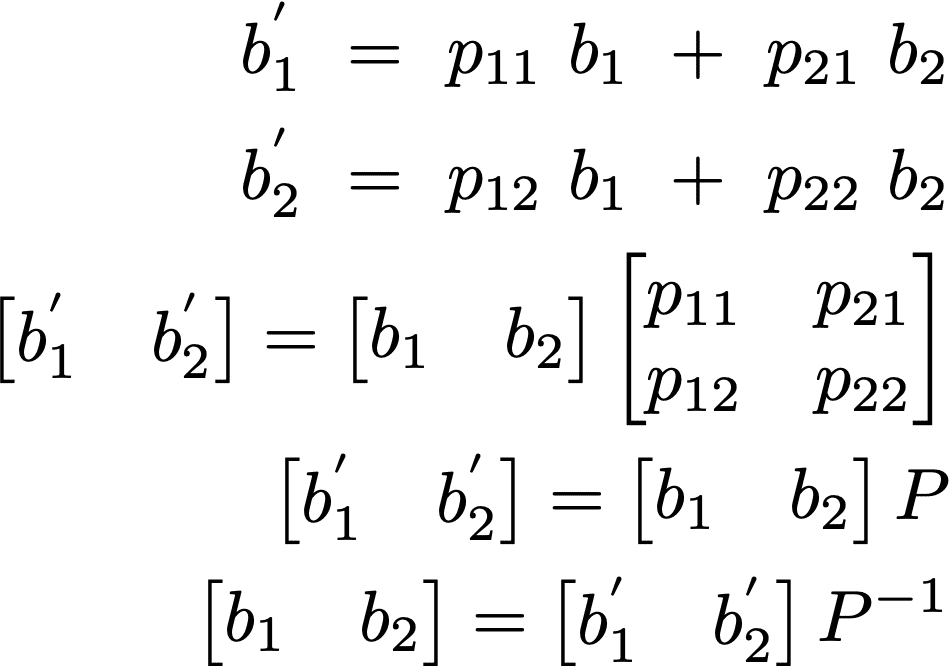
・直交行列
基底の変換行列Pが 転置をとったtPとの積が単位行列となるときその正方行列を直行行列という。
tP x P = E
こうなるとき、この基底は正規直交基底となる。
逆に言えば、正規直交基底の変換行列は直交行列。
更に言えば、正規直交基底から基底への変換行列が直交行列のとき、もう一方の基底も正規直交基底となる。
・表現行列
線形写像Tとするときの、
基底b1 , b2 , .... bnの線形変換の像[T(b1),T(b2), .... , T(bn)]を
[b1 b2 .... bn]A(表現行列)
の積の形で表したAを基底b1,b2, .... , bnに関する線形写像Tの表現行列という。
ようするに、基底の各ベクトルの像の、その基底自身に関する成分表示による成分を列ベクトルとした行列が表現行列である。
感覚としては、(全く定義ではない)変換行列の像版みたいな感じ。
・余因子行列
A A' = A' A = |A|E = |A|を成分とした対角行列
となるようなA'のことを余因子行列という。
A'の成分は余因子展開によって求めることができる。
逆行列を余因子行列と行列式を使って出すことがdケイル
・転置行列
行列Aの各行を、列に並び替えてできる行列をAの転置行列という
記号tAと左上にtをつけ表される。
各列を行に並び替えたといっても同じことである。
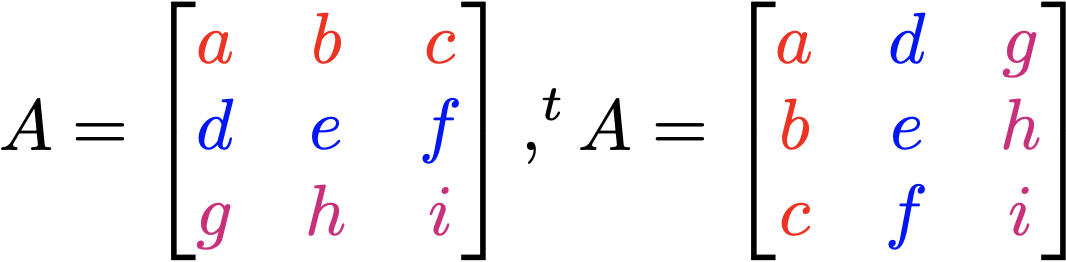
・逆行列
n次正方行列Aに対し、
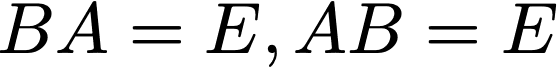
となる正方行列Bが存在する時、Aは正則であるといい、BをAの逆行列という。
逆行列はいつでも存在するとは限らなく、様々な方法で確認することができる。簡単な例だと、行列式が0でない正方行列は正則である。
・正方行列
行の個数と列の個数が等しい行列 n × n行列をn次正方行列という。
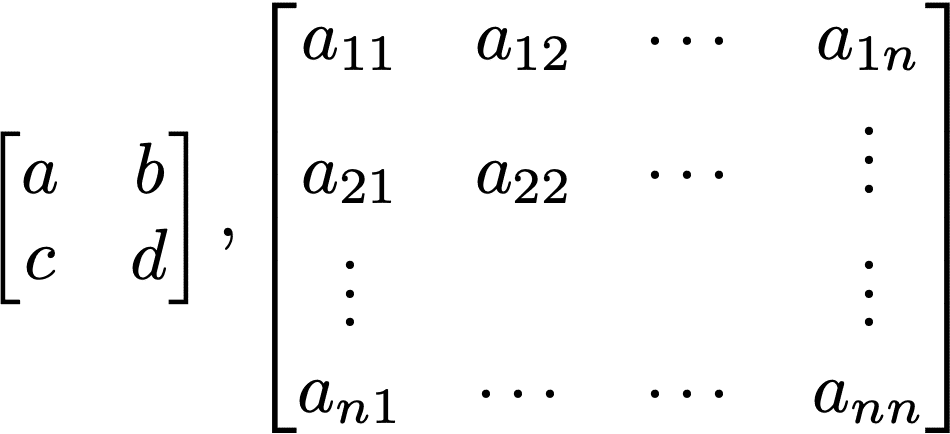
・対角行列
対角成分 : 正方行列において左上から右下への対角線上に並ぶ成分
a11,a22,a33 ..... ann
対角成分以外の成分が全て0である正方行列を対角行列という。
正方行列A = [aij]において i ≠ jのとき、aij = 0となるときAを対角行列という。
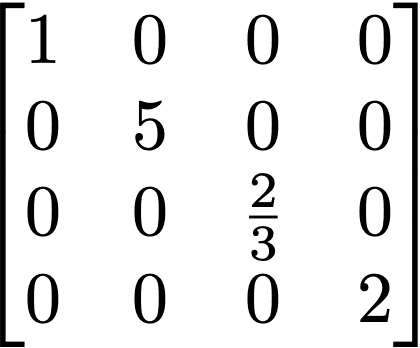
・単位行列
対角成分がすべて1である対角行列を単位行列という。
よくEで表される。
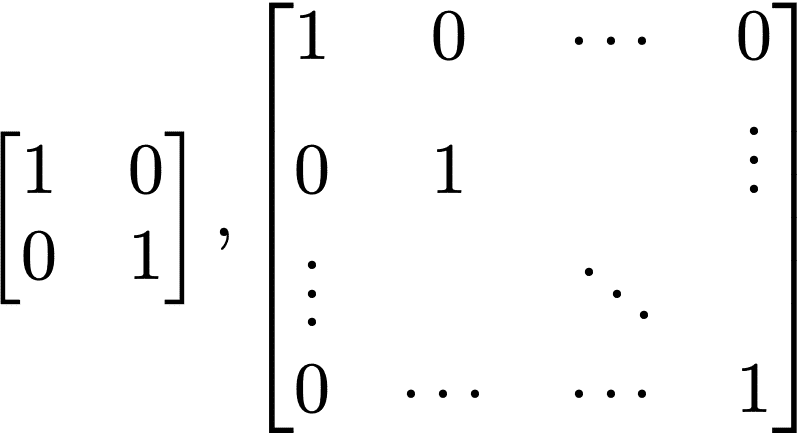
・対称行列
正方行列AにおいてAの転置行列と等しいとき、対称行列という。
つまり、対角行列を軸として対象な形になっている行列といえる。
対角行列は対称行列といえる。E:単位行列も典型的な対称行列。
反対称行列というtA = -Aになる行列もある。
反対称行列は一般に、対角成分は全て0である。
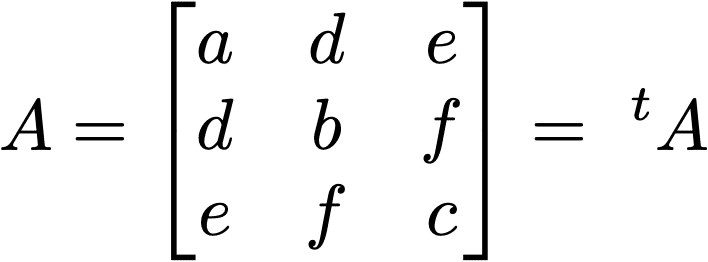
・階段行列
次の二つの条件を満たす行列をいう。
(1)零ベクトルである行は、まとめて一番下の行にある
(2)零ベクトルでない行については、行番号が増えるに連れて左端から連続して並ぶ0の個数が増えていく。
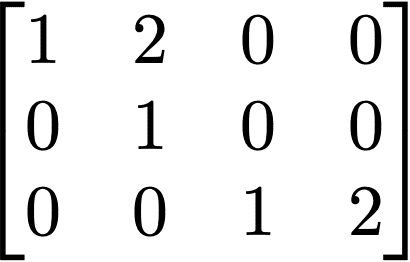
・係数行列
連立一次方程式の左辺の係数全体の作る行列
連立1次方程式を行列の形やベクトルの形であらわしたとき、
Ax = bとなるとき、これを係数行列という。
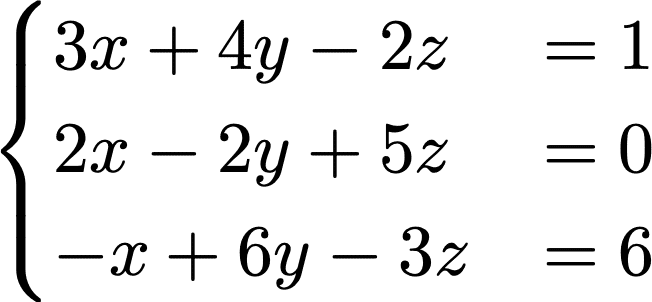
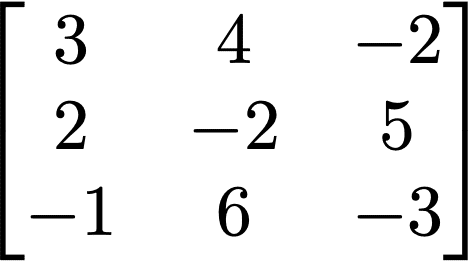
・拡大係数行列
連立一時方程式の係数全体のつくる行列
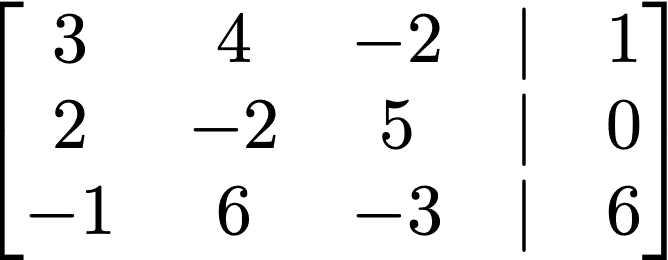
・三角行列
A=[aij] i > jのときaij = 0、 i < jのときaij = 0
これらをそれぞれ、上三角行列、下三角行列という。
https://mathtrain.jp/triangularmatrix
[用語]**変換
・線形変換
線形写像の中で、R^n → R^n や V → V となるような線形写像を線形変換(1次変換)という。
・直交変換
ベクトル空間R^nの線形変換Tで内積を保つ変換を直交変換という。すなわち二つの任意のベクトルa,b ∈ R^nに対して
T(a) ・ T(b) = a・b
を満たす線形変換を直交変換という。
[用語]**空間
・ベクトル空間
n次数ベクトル全体のつくる集合をR^nとで表し、演算も同時に考えたようなものをR^nをn次ベクトル空間という。
単に”ベクトル空間”というときは、数ベクトル空間や部分空間を指すことをにする
・部分空間
ベクトル空間R^nの空集合でない部分集合としてWがあった時、次の条件を満たすものをR^nの部分空間という
(1)Wの任意の2つのベクトルa, bに対して、和a+bもWに含まれる
i.e a, b ∈ W → a+b ∈ W
(2)任意のスカラーkと任意のa ∈ Wに対して、スカラーk倍kaもWに含まれる。
i.e k ∈ R ,a ∈ W → ka ∈ W
・解空間
Aがm x n行列の時、同時連立1次方程式 Ax = 0
の解全体をつくる集合をWとおく、すなわち
W = {a ∈ R^n | Aa = 0}
このときWはR^nの部分空間となって、このWをAx = 0の解空間という。
・零空間
零ベクトルだけからなる部分集合{0}を零空間という。
・自明な部分空間
R^n自身もR^nの部分空間である。
零空間やR^nのような部分空間を自明な部分空間という。
・固有空間
固有ベクトルは次の方程式の自明でない解である。
A(定義行列), λ(Aの固有値), E(単位行列), x(固有ベクトル)
(A - λE)x = 0
この同時連立1次方程式の会空間をWλといき、Aのλに対する固有空間という
Wλ = {x | (A - λE)x = 0 }
[用語]**ベクトル
・法線ベクトル
ベクトルn = (a,b,c),ベクトルx = (x,y,z)の内積が0(直交)しているとき、
ax + yb + zc = 0と表現できて、
この解はベクトルnと直交し、解空間W0を考えた時この平面と垂直なベクトルnと表現もできる。
1次方程式 ax + yb + zc = dを考えた場合でも、上記のWの平行移動したものなのでnであるということは変わらない。
このベクトルnを平面ax + yb + zc -d = 0の法線ベクトルという。
座標平面上の直線についても同様に定義される。
端的に言えば、平面に対して垂直なベクトルとかを法線ベクトルという。
・固有ベクトル
n次正方行列Aに対して、次の等式を満たすスカラーλと列ベクトルuが存在したとする
Au = λu
この時のλを固有値といい、uをλに対するAの固有ベクトルという
線形写像T、線形変換をTAと表した時の
λをT(TA)の固有値といい、uをλに対するT(TA)の固有ベクトルともいった言ったりする。
これらは行列の対角化をする際に利用できるものである。
・数ベクトル
・行ベクトル
行列の中で特に1行だけの行列、すなわち1 x n行列をn次の行ベクトルという。
・列ベクトル
行列の中で特に1列だけの行列、すなわちm x 1行列をm次の列ベクトルという。
・零ベクトル
成分が全て0である行ベクトルや列ベクトルを零ベクトルという。
記号0でよく表される。
・幾何ベクトル
・単位ベクトル
ベクトルの大きさが1のベクトル。
・方向ベクトル
同次1次方程式の解空間Wのベクトルを方向ベクトルという(?)
端的に言えば、方向を表すようなベクトルという。
・基本ベクトル
x , y ,zのような座標軸に対して、正の方向に平行な単位ベクトルなものを基本ベクトルという。
基本ベクトルは1次独立である。
その他[用語]
・同次連立一次方程式
定数項がすべて0である連立1次方程式
Ax = 0 (xはベクトル、0は零ベクトル、Aは行列)
自明な解
x1 = x2 = .... = xn = 0,すなわち、**x **= **0 **は明らかに上の同時連立一次方程式の解である。この解を自明な解という。
・階数 / rank
階段行列において、零ベクトルでない行の個数をその行列の階数といいrank(A)で表す。
・基底
任意のベクトル空間Vのベクトルb1 , b2, b3, .... ,bp(1 <= p <= n)で次の条件を満たすものをVの基底という。
(1)b1 , b2, b3, .... ,bpが1次独立(線型独立)
(2)Vの任意のベクトルはb1 , b2, b3, .... ,bpの1次結合で表される(b1 , b2, b3, .... ,bpでVを生成する)
同じベクトル空間でも基底の組みはいくらでも存在する
色々定理が展開されており、
簡単なものでいうならば、 R^nのベクトル空間においては、n個の基底が存在する
・正規直交基底
ベクトル空間のR^nのn個の基底で次の条件を満たすものをいう。
(1)|bi| = 1 (i = 1,2,3...n) つまり、各基底ベクトルは単位ベクトル。
(2)i≠jのとき、bi ・ bj = 0, すなわち、異なる二つのベクトルbiとbjは直行する。
標準基底e1, e2, ..... e3 は正規直交基底。
・標準基底
x,y,z軸のような基準となる軸に対して正の方向に平行な基底ベクトルをいう。
[1 0 0 0 ], [0 1 0 0],[0 1 0]
・次元
ベクトル空間Vの基底ベクトルの個数は一定である。
dim(V) = Vの基底のベクトルの個数とおき、
これを次元という。
零空間{0}の次元0と定める
この記事が気に入ったらサポートをしてみませんか?
