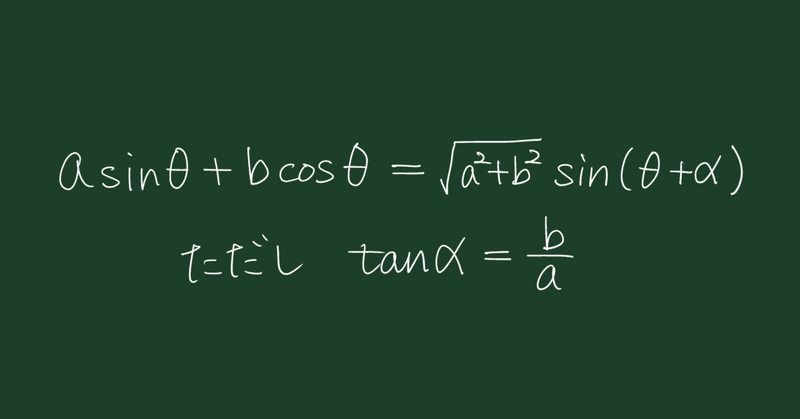
いい証明を思いついた②〈三角関数の合成〉
三角関数の合成は、急に尋ねられると、戸惑う。
「あれ、どんな式だったかな……?」
(カキカキ……)

「そうそう、こんな感じ」
でもこれ、どうやって証明するんだっけ?
この式は、右辺に加法定理を使うと証明することができる。tanα = b/a を“信じて”、cosαとsinαを求めて代入すれば、左辺と等しくなることが確認できる。
しかし、この証明は合成後の関数から逆戻りするスタイルなので、左辺から右辺を導くことができない。そのため、公式を覚えていなくてはならないのが厄介だ。
そうか、こればかりは暗記しなきゃいけないのか。
数学は暗記科目ではないはずなのに……。
覚え方
たしか、高校時代、次のような図を書いて覚えさせられたのだった。

下の辺の長さが a、右の辺の長さが b の、tanα= b/a を満たす直角三角形を作る。一見、本題とは関係なさそうなこの三角形において、斜辺の長さと角度αが、合成関数の係数を決定している。
どうしてこれでうまくいくの?
なぜこれでうまくいくのか、長い間考えたことがなかった。当たり前のものとして受け入れてしまっていたのだ。
これは考え直す必要がある。もしかすると、右辺から左辺へ逆戻りしない、ストレートな証明が見つかるかもしれない。
この三角形は、2つのパラメータ(a , b)を与えただけで、2つのほしい変数が完全な形で返ってくる。これは、偶然とは思えない。
やはり、この三角形を軸に、三角関数に結びつけて考えるのがよいだろう。
図を、少し書き直してみる。

こうすると、ベクトルの和に見えなくもない。
長さが a のベクトルと、長さが b のベクトル。これらが合成されて、長方形の対角線上に、長さが √(a^2+b^2) のベクトルができている。
「!」
ここで閃いた。
「これを、XY座標に置いて、θだけ回転させてみたらどうなる???」

まず、3つのベクトルの始点を座標原点にセットする。(図では、見やすさのためにベクトルの矢印は省略している)
次に、これをθだけ左に回転させる。

ここで、各ベクトルの y 成分の値に注目してほしい。
するとどうだろう。
答えはもう、ほとんど得られている!
長さが a のベクトルの y 成分は a sinθ
長さが b のベクトルの y 成分は b cosθ
合成されたベクトルの y 成分は √(a^2+b^2) sin(θ+α)
合成ベクトルの y 成分は、もとのベクトルの y 成分どうしの和によって計算されるので、
a sinθ+ b cosθ= √(a^2+b^2) sin(θ+α)
である。

よって証明は完了した。
なんと、三角形をθ回転させるだけでよかったのだ!
あの三角形は、覚えるための単なる方便ではなかった。
意味を持たせることが、できたのだ。
つまりどういうこと?
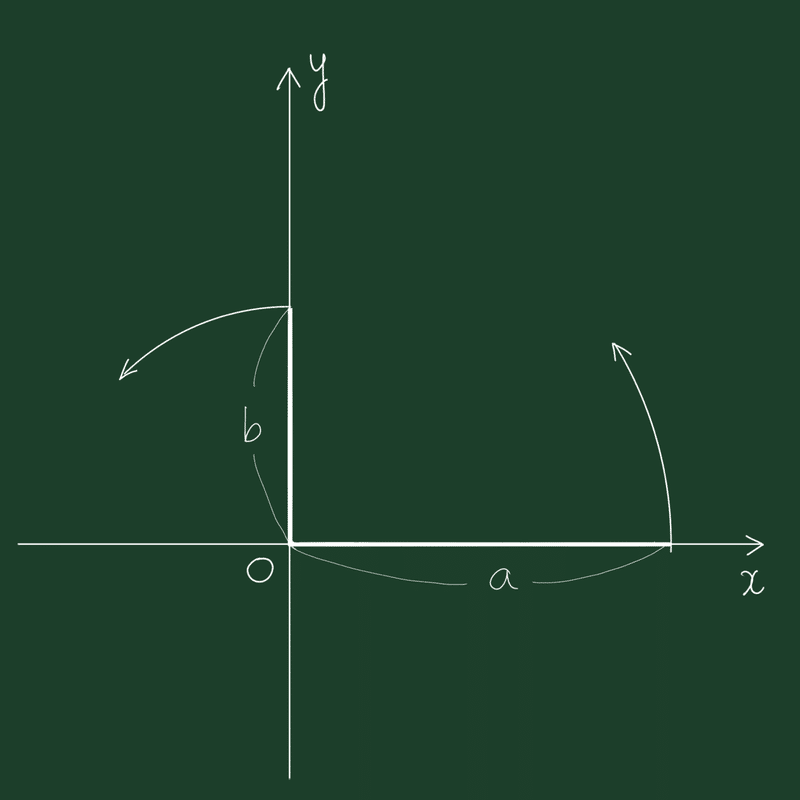
a sinθは、長さ a の棒が x 軸上(θ= 0°)から左に回転したときの、棒の先端の高さを表している。(sin関数は、0から1に向かって上昇する。)
一方、b cosθは、長さ b の棒が y 軸上(θ= 90°)から左に回転したときの、棒の先端の高さを表している。(cos関数は、1から0に向かって下降する。)
つまり、求めたい値、a sinθ+ b cosθは回転する2つの棒の高さの和である。

しかし、回転させる前に、2つの棒を合成して斜めの棒を作ってから(ベクトル和)、それを回転させて高さを測っても同じ値が得られるはずだ。
なぜなら、合成ベクトルの y 成分は、y 成分どうしの和で得られるからだ。
この斜めの棒の長さは√(a^2+b^2)で、初期角度はαである。
だから、この棒の先端の高さは√(a^2+b^2) sin(θ+α) で与えられる。
あとは長さ b の棒を右に平行移動して直角三角形を作れば、暗記用の三角形ができる。
今回も、いい証明を思いついた。
この記事が気に入ったらサポートをしてみませんか?
